Péndulo | Movimiento oscilatorio | Física | Khan Academy en Español

Summary

En este video, se explica cómo el péndulo simple, compuesto por una masa conectada a un hilo, puede considerarse un oscilador armónico simple en ciertos casos. Se analiza su comportamiento y se compara con un sistema de masa y resorte, destacando cómo factores como la longitud del hilo y la aceleración gravitacional afectan el periodo de oscilación. Además, se aclara que, para ángulos pequeños (menos de 20 grados), el péndulo sigue muy de cerca las leyes de un oscilador armónico simple, y se presenta la fórmula para calcular su periodo. Finalmente, se detalla cómo las pequeñas variaciones de amplitud no afectan significativamente el periodo en estos casos.

Takeaways

• 😀 Un péndulo simple es un ejemplo común de oscilador armónico simple, con un movimiento similar al de una masa en un resorte.
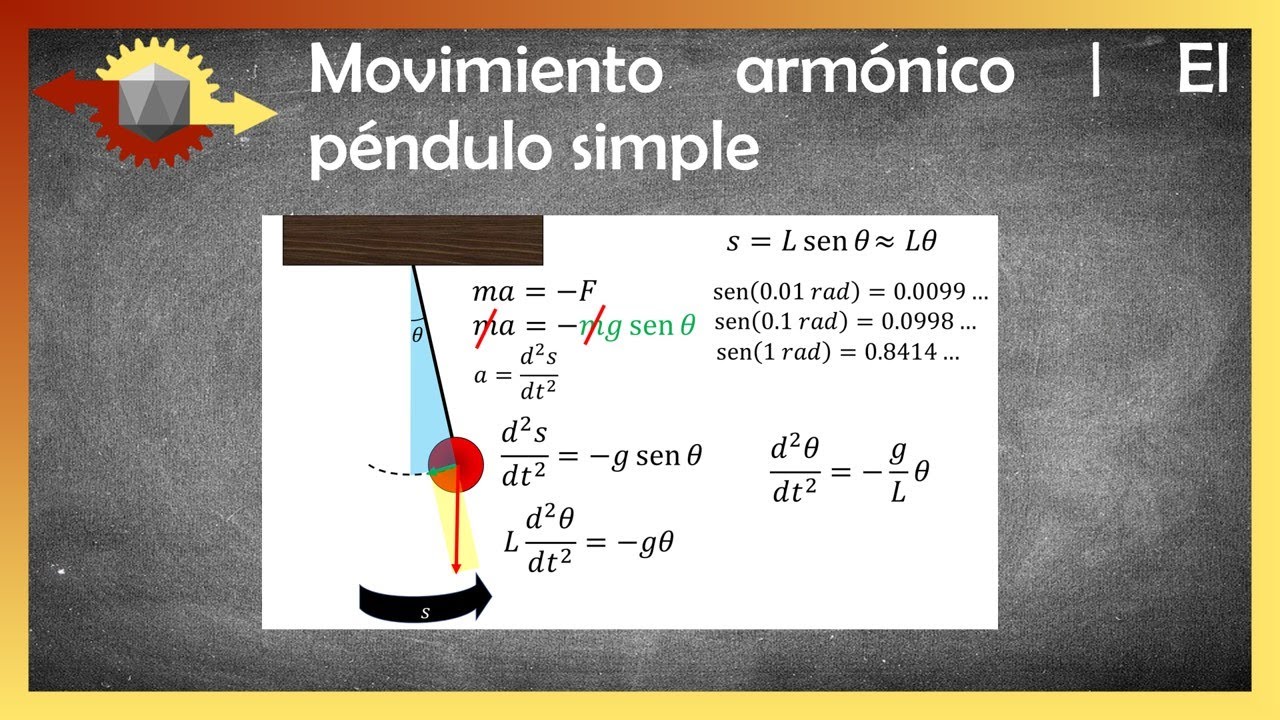
• 😀 El péndulo simple se describe mediante un ángulo de desplazamiento (θ) en lugar de una distancia lineal, lo que lo convierte en un oscilador armónico con desplazamiento angular.
• 😀 Para ángulos pequeños (menos de 20°), el péndulo se comporta de manera muy similar a un oscilador armónico simple, y su periodo puede describirse con la fórmula T = 2π √(l/g).
• 😀 La masa del péndulo no afecta el periodo, ya que el aumento de la masa también aumenta la fuerza gravitatoria, lo que balancea el efecto sobre la velocidad de oscilación.
• 😀 El periodo del péndulo depende del largo de la cuerda (l) y de la aceleración debida a la gravedad (g), pero no de la masa del objeto.
• 😀 El periodo del péndulo aumenta con el largo de la cuerda, ya que una mayor longitud aumenta el momento de inercia, dificultando el movimiento del péndulo y alargando el tiempo de oscilación.
• 😀 Si aumentamos la aceleración gravitacional (g), el periodo disminuye, ya que la mayor fuerza gravitatoria provoca una mayor aceleración, haciendo que el péndulo se mueva más rápido.
• 😀 El ángulo de desplazamiento (amplitud) no afecta el periodo del péndulo si el ángulo es pequeño, pero para ángulos grandes, la fórmula deja de ser válida y el periodo comienza a depender de la amplitud.
• 😀 Para ángulos menores a 20°, el error en la aproximación de la fórmula es menor al 1%, pero para ángulos mayores (hasta 70°), el error puede llegar al 10%.
• 😀 El péndulo simple es un buen ejemplo de cómo los osciladores armónicos simples pueden ser aproximados para ángulos pequeños, y la fórmula para el periodo es útil en esas condiciones.
• 😀 A pesar de ser similar a los osciladores armónicos simples, el péndulo se comporta de manera diferente a medida que los ángulos de desplazamiento aumentan, lo que genera una mayor desviación en el cálculo del periodo.

Q & A

¿Por qué un péndulo simple puede considerarse un oscilador armónico simple?

Un péndulo simple puede considerarse un oscilador armónico simple porque tiene una fuerza restauradora proporcional al desplazamiento, lo que le permite seguir un movimiento oscilatorio similar al de un sistema de masa y resorte.

¿Qué es la diferencia entre un péndulo simple y un péndulo doble?

El péndulo simple tiene una masa conectada a un hilo y se mueve de manera predecible. En cambio, el péndulo doble es más complejo, con dos masas interconectadas y su movimiento es caótico, lo que lo hace más difícil de describir matemáticamente.

¿Cuál es el rol de la amplitud en el movimiento de un péndulo simple?

Para un péndulo simple, la amplitud o el ángulo máximo de desplazamiento influye en la magnitud del movimiento, pero no afecta el periodo del péndulo siempre y cuando el ángulo sea pequeño (menor a 20 grados).

¿Qué variable describe el movimiento de un péndulo en lugar de 'x'?

En el caso de un péndulo, la variable que describe el movimiento no es 'x', sino el ángulo de desplazamiento, denominado 'theta'. Este ángulo varía con el tiempo a medida que el péndulo oscila.

¿Por qué el periodo de un péndulo simple no depende de la masa?

El periodo de un péndulo simple no depende de la masa porque los efectos de la mayor inercia de la masa y la mayor fuerza gravitacional se compensan entre sí. A pesar de que un aumento de la masa aumenta la inercia y la fuerza de gravedad, ambos efectos se cancelan, dejando el periodo sin cambios.

¿Qué afecta el periodo de un péndulo si no es la masa?

El periodo de un péndulo depende principalmente de la longitud del hilo (L) y la aceleración debida a la gravedad (g). Aumentar la longitud del hilo aumenta el periodo, mientras que un aumento en la gravedad disminuye el periodo.

¿Cómo se relacionan el momento de inercia y el periodo de un péndulo?

El momento de inercia, que depende de la masa y la longitud del hilo, determina cuán difícil es mover el péndulo. Un mayor momento de inercia hace que el péndulo tarde más en completar un ciclo, lo que aumenta el periodo.

¿Cómo influye la aceleración gravitacional en el periodo de un péndulo?

Aumentar la aceleración gravitacional reduce el periodo del péndulo. La mayor fuerza de gravedad causa una mayor aceleración y velocidad del péndulo, lo que permite completar el ciclo en menos tiempo.

¿Por qué el periodo del péndulo se ve afectado por la longitud del hilo?

La longitud del hilo afecta el momento de inercia del péndulo. Una mayor longitud hace que el péndulo sea más difícil de mover, aumentando su momento de inercia, lo que a su vez aumenta el periodo.

¿Qué diferencia hay entre un oscilador armónico simple en un péndulo y uno con un resorte?

Tanto un péndulo simple como un sistema masa-resorte comparten una estructura similar en cuanto a su dependencia de la inercia y las fuerzas restauradoras. Sin embargo, en el péndulo, la fuerza restauradora está dada por la gravedad, mientras que en un resorte es la constante del resorte. Ambos sistemas tienen una ecuación de periodo similar, pero con diferentes factores que afectan el movimiento.