Bloque 2 Producto Punto
Summary
TLDR本视频讲解了向量的点积(又称标量积)的概念。首先,介绍了点积的数学定义,即两个向量的模长乘积与它们之间角度余弦的乘积,结果为标量。接着,讲解了通过分量计算点积的操作定义,并通过具体例子演示了如何计算。视频还展示了如何结合数学定义与操作定义求解向量之间的夹角,并介绍了点积为零时向量的正交性原理。最后,总结了点积在几何中的应用,强调了向量正交的重要性。
Takeaways
- 😀 点积(又称标量积)是两向量相乘得到一个标量的数学运算。
- 😀 点积的数学定义是:两个向量的模长相乘,再乘以它们之间夹角的余弦。
- 😀 通过操作性定义,点积可以通过向量的各分量相乘后求和得到。
- 😀 点积的操作性定义公式:a·b = ax * bx + ay * by + az * bz。
- 😀 示例计算:如果 a = 3i + 5j - 2k,b = 9i - 3j + 8k,则 a·b = 27 - 15 - 16 = -4。
- 😀 点积不仅能得到标量值,还可以用来计算两个向量之间的夹角。
- 😀 通过结合数学定义与操作性定义,可以求得两个向量之间的夹角:cosθ = (a·b) / (|a| * |b|)。
- 😀 示例计算夹角时,首先需要计算两个向量的模长,然后使用反余弦函数求得夹角。
- 😀 例如,计算向量a和b的夹角,结果为92.90°。
- 😀 点积的一个重要特性是:当两个向量的夹角为90°时,点积为0,这表明它们是正交的(垂直)。
Q & A
什么是点积(producto punto)?
-点积,也称为标量积,是向量的乘法运算,结果是一个标量(即数字),而不是向量。
点积的数学定义是什么?
-点积的数学定义为两个向量A和B的模长相乘,再乘以它们之间角度的余弦值,即 A·B = |A| × |B| × cos(θ)。
什么是点积的操作性定义?
-操作性定义指出,点积是通过两个向量的对应分量相乘并求和来计算的。例如,A·B = Ax × Bx + Ay × By + Az × Bz。
如何计算两个向量的点积?
-计算点积时,将两个向量的相应分量相乘并加总。例如,对于向量A = 3i + 5j - 2k和B = 9i - 3j + 8k,点积为 3×9 + 5×(-3) + (-2)×8 = -4。
如何计算两个向量之间的夹角?
-两个向量之间的夹角可以通过点积和向量的模长来计算,公式为 θ = cos⁻¹(A·B / (|A| × |B|))。
如何求得向量的模长?
-向量的模长是每个分量的平方和的平方根。例如,向量A = 3i + 5j - 2k的模长为√(3² + 5² + (-2)²) = √38。
点积计算中,cos(θ)等于什么?
-cos(θ)是两个向量夹角的余弦值。当向量之间的角度为90度时,cos(θ)为0。
如果两个向量的点积为零,这意味着什么?
-如果两个向量的点积为零,则这两个向量是正交的,也就是说它们是垂直的。
点积与向量的角度之间有什么关系?
-点积可以用来计算两个向量之间的角度,角度θ可以通过公式 θ = cos⁻¹(A·B / (|A| × |B|)) 计算。
为什么当两个向量的夹角为90度时,点积为零?
-当两个向量的夹角为90度时,cos(90°) = 0,因此点积的结果也为零。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

CCIR - Quantum Physics: Information, Foundations And Gravity - TA Session #1

Teorema fundamental del cálculo: definición y ejemplos

Natuurkunde uitleg DICHTHEID ALGEMEEN
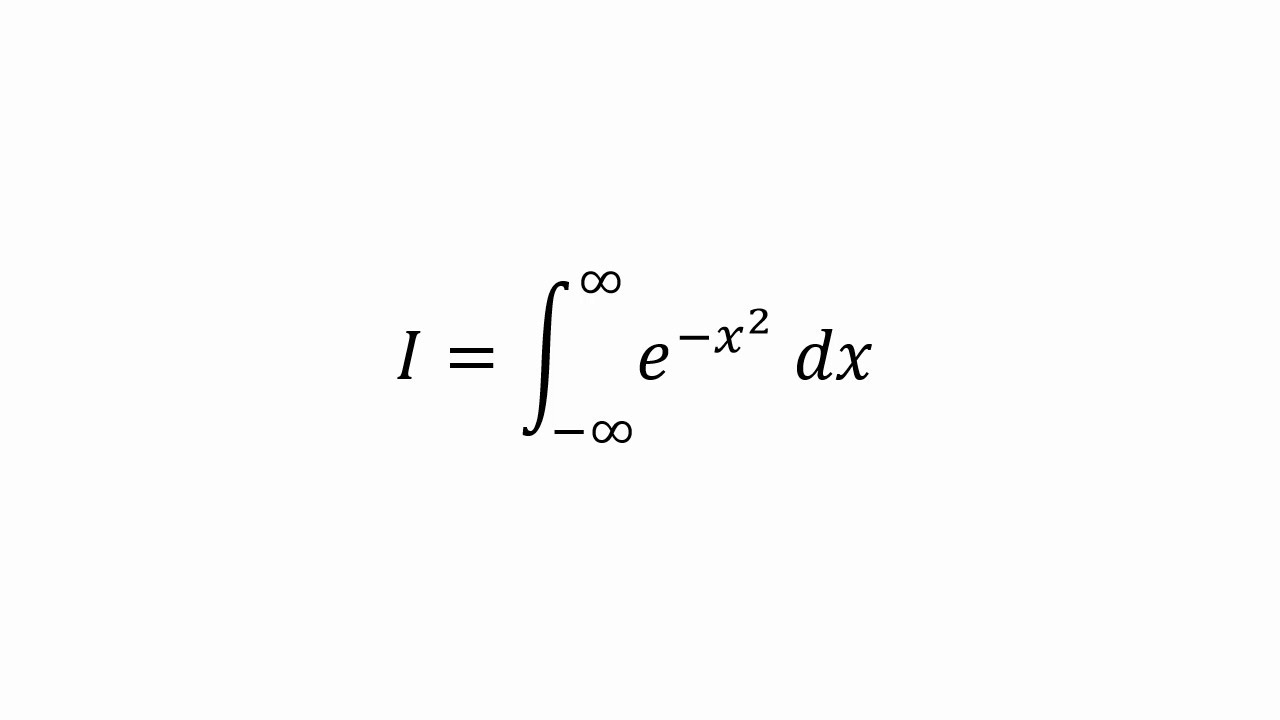
The Gaussian Integral

Introduction to linear independence | Vectors and spaces | Linear Algebra | Khan Academy

CCIR - Quantum Physics: Information, Foundations And Gravity - Lecture Session #2

Emoji Trading Order Flow Video Series 4: Absorption - act upon the market's reaction.
5.0 / 5 (0 votes)