Maximum volume cylinder, using DERIVATIVES (Optimization)
Summary
TLDR在本视频中,作者通过一个实际应用的数学问题展示了如何利用导数来优化一个圆柱体的尺寸。题目要求用2480平方厘米的材料制作一个没有盖子的圆柱体,目的是最大化容积。通过构建公式并运用导数方法,作者推导出了圆柱体的最优半径和高度。整个过程不仅帮助观众理解了如何在数学中应用导数,还通过实际问题提升了数学思维。最后,作者还介绍了自己的应用程序,鼓励观众下载并通过练习提升数学技能。
Takeaways
- 😀 本视频介绍了一个通过导数解决的应用题,目的是找到使容器体积最大化的圆柱体尺寸。
- 😀 问题要求在给定的表面积(2400平方厘米)下,找出圆柱的半径和高度。
- 😀 视频强调这是一个优化问题,主要目标是最大化圆柱的体积。
- 😀 为了求解问题,首先需要记住圆柱的体积公式:V = π * r² * h。
- 😀 为了简化问题,需要消除两个未知数(半径r和高度h),因此引入了表面积的约束条件。
- 😀 通过计算表面积的公式,将面积分成侧面积和底面积,并得到了包含r和h的方程。
- 😀 视频选择解出高度h,而不是半径r,以便将其代入体积公式中简化计算。
- 😀 最终得到了一个只包含r的体积表达式,为了最大化体积,视频使用了导数进行优化。
- 😀 通过求导数并找到临界点,找到了一个可能的最大值点。使用二阶导数判断该点确实是最大值。
- 😀 计算出半径r的值,并代入到之前的高度公式中,最终得到了圆柱的半径和高度的精确数值。
- 😀 结果表明,圆柱的半径和高度应该是相等的,并且最终值约为16.22厘米。
- 😀 该视频还强调了通过多做练习来加深对数学概念的理解,并推荐使用专门的应用程序来辅助学习。
Q & A
这个问题的背景是什么?
-这个问题要求我们设计一个没有顶部的圆柱形容器,使用2,480平方厘米的材料,并要求我们确定容器的半径和高度,以使容器的体积最大化。
如何计算圆柱体的体积?
-圆柱体的体积可以通过公式V = πr²h计算,其中r是圆柱的半径,h是圆柱的高度。
这个问题的约束条件是什么?
-问题的约束条件是使用2,480平方厘米的材料,这个面积不包括顶部。因此,材料的总面积是圆柱的侧面积加上底面积。
如何得到圆柱体的表面积公式?
-圆柱的表面积由两部分组成:侧面积和底面积。侧面积的公式是2πrh,底面积的公式是πr²。因此,表面积公式为2πrh + πr²。
如何将两个变量r和h消除,进而进行优化?
-为了消除r和h中的一个变量,我们使用给定的面积约束公式2πrh + πr² = 2,480,解出h并代入体积公式中,从而得到只依赖r的体积公式。
如何通过体积公式进行最大化优化?
-首先,我们将高度h代入体积公式得到一个仅包含r的体积公式。然后,求这个体积公式的导数,并找到导数为零时的r值,即为可能的最大值点。
如何证明得到的r值是最大值而不是最小值?
-通过计算第二导数并检查它的符号来确认。若第二导数为负,则表示在该点取得最大值。
第二导数检验的作用是什么?
-第二导数检验用于确定在某个临界点是取得最大值还是最小值。如果第二导数为负,则该点是最大值点,若为正则是最小值点。
如何通过第二导数验证最大体积?
-我们计算第二导数并将其代入r值,若结果为负数,说明此时体积达到最大值。
最后得出的最佳半径和高度是多少?
-最佳的半径和高度都为16.22厘米,这个尺寸能够使圆柱体的体积最大化,满足给定的材料面积约束。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Problema de OPTIMIZACIÓN resuelto utilizando la derivada / (Nivel: Medio Alto)

Better AI Agents Solving MATH Problems | AutoGen MathAgent

Derivada de un producto | Ejemplo 3

Python Advanced AI Agent Tutorial - LlamaIndex, Ollama and Multi-LLM!
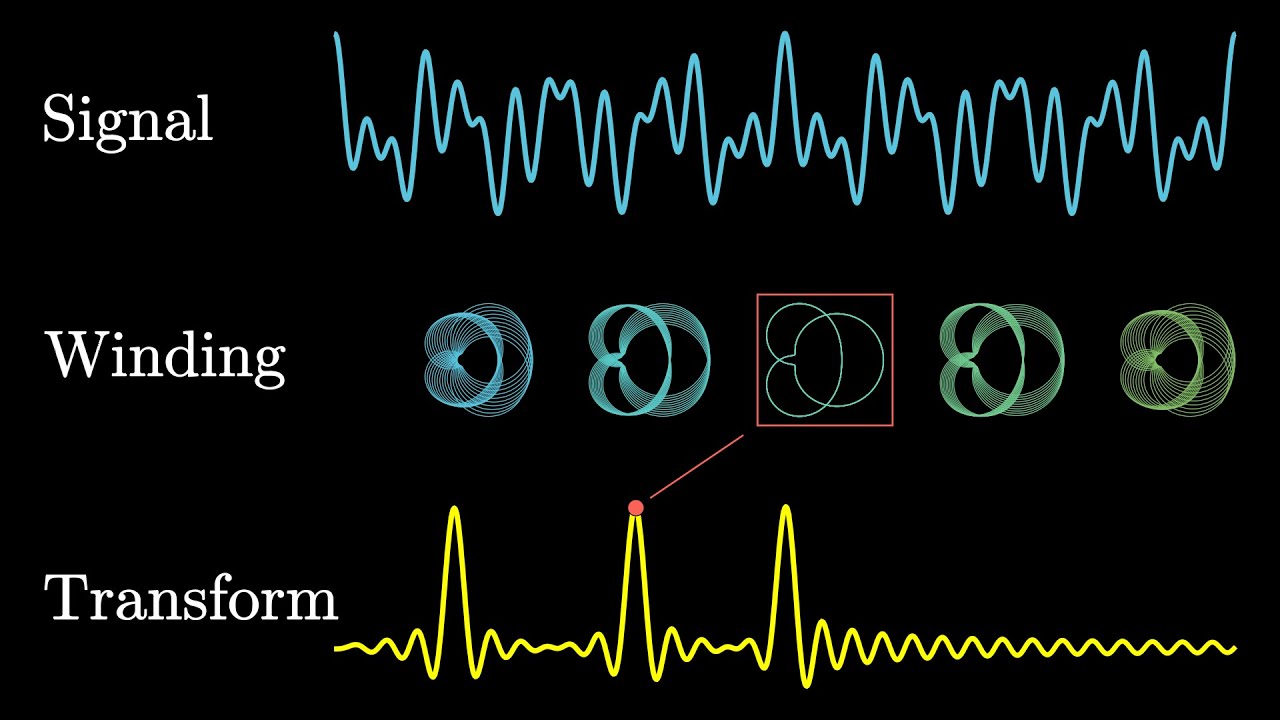
But what is the Fourier Transform? A visual introduction.

How to Use LangSmith to Achieve a 30% Accuracy Improvement with No Prompt Engineering

Multiple JDBC Clients - How to configure multiple DataSources in Spring
5.0 / 5 (0 votes)