Dinamika Fluida
Summary
TLDRThis video lecture covers fundamental concepts in fluid dynamics, focusing on key equations such as the Continuity Equation and Bernoulli's Equation. It explains the relationship between fluid velocity, pressure, and area, and demonstrates practical applications through problems involving pipes and flow rates. The lecture also discusses the use of Pitot tubes for measuring fluid velocity and highlights how fluid dynamics principles apply to real-world scenarios like fluid flow in pipes and tanks. The session provides detailed examples and step-by-step solutions to reinforce the concepts.
Takeaways
- 😀 The lesson focuses on the topic of Fluid Dynamics, following a previous session on Fluid Statics.
- 😀 Fluid Dynamics includes key concepts such as the Continuity Equation and Bernoulli's Equation.
- 😀 The Continuity Equation expresses the conservation of mass, stating that the mass flow rate remains constant in a fluid system (A1 * V1 = A2 * V2).
- 😀 The Bernoulli Equation describes the relationship between pressure, velocity, and elevation in a flowing fluid, taking into account energy conservation.
- 😀 The equation for Bernoulli’s Principle is: P1 + 1/2 * rho * V1^2 + rho * g * h1 = P2 + 1/2 * rho * V2^2 + rho * g * h2.
- 😀 Practical examples illustrate how fluid flow behaves in pipes with varying cross-sectional areas and the corresponding changes in speed and pressure.
- 😀 The flow rate (Q) is calculated by multiplying the cross-sectional area (A) by the velocity (V), with units converted appropriately (e.g., from cubic meters per second to cubic meters per hour).
- 😀 The speed of fluid increases when flowing through narrower sections of a pipe, demonstrating the principle of conservation of mass in fluid dynamics.
- 😀 In a tank with a fluid flowing through a hole, the fluid's velocity can be calculated using Bernoulli's equation, considering the height difference and the acceleration due to gravity.
- 😀 The lesson also covers practical applications of Bernoulli’s principle, such as using a Pitot tube to measure fluid velocity by evaluating the pressure difference in the fluid.
Q & A
What is the continuity equation in fluid dynamics?
-The continuity equation in fluid dynamics states that the mass flow rate of a fluid is constant along a streamline. It is mathematically expressed as A1 * V1 = A2 * V2, where A1 and A2 are the cross-sectional areas at two points, and V1 and V2 are the velocities at those points.
How does the continuity equation relate to the velocity of a fluid in different sections of a pipe?
-The continuity equation shows that as the cross-sectional area of a pipe decreases, the velocity of the fluid must increase to keep the mass flow rate constant. This is why water moves faster through a narrower pipe compared to a wider one.
What is Bernoulli's equation and how is it used in fluid dynamics?
-Bernoulli's equation relates pressure, velocity, and height in a flowing fluid. It is expressed as P1 + 1/2 * ρ * V1² + ρ * g * h1 = P2 + 1/2 * ρ * V2² + ρ * g * h2, where P1 and P2 are the pressures at points 1 and 2, V1 and V2 are the velocities, and h1 and h2 are the heights. It is used to analyze the energy transformations in a fluid flow.
What does Bernoulli's equation imply about the relationship between pressure and velocity in a fluid?
-Bernoulli's equation implies that as the velocity of a fluid increases, its pressure decreases, and vice versa. This is a direct consequence of the conservation of mechanical energy in a fluid flow.
How can you calculate the velocity of a fluid at the bottom of a tank using Bernoulli's equation?
-Using Bernoulli’s equation, the velocity of a fluid at the bottom of a tank can be calculated as V = √(2 * g * h), where g is the acceleration due to gravity and h is the height of the fluid above the bottom. This equation assumes the velocity at the surface is zero.
What is the significance of the Pitot tube in fluid dynamics?
-The Pitot tube is used to measure the velocity of a fluid by measuring the difference between the static and dynamic pressures. The velocity is then calculated using the formula V = √(2 * (P1 - P2) / ρ), where P1 is the static pressure, P2 is the dynamic pressure, and ρ is the fluid density.
What is the relationship between the cross-sectional area and the velocity of a fluid based on the continuity equation?
-According to the continuity equation, the velocity of a fluid is inversely proportional to the cross-sectional area. If the area decreases, the velocity increases, and if the area increases, the velocity decreases, assuming the mass flow rate remains constant.
How is the concept of fluid flow rate related to the dimensions of the pipe?
-Fluid flow rate is directly related to the cross-sectional area and the velocity of the fluid. The flow rate (Q) is given by the product of the area (A) and the velocity (V) of the fluid, i.e., Q = A * V. A larger cross-sectional area or higher velocity leads to a higher flow rate.
In the example problem with a pipe having different cross-sectional areas, how do you calculate the flow rate and velocity at different sections?
-The flow rate (Q) at each section of the pipe is the same because of the continuity equation. First, calculate the flow rate using Q = A1 * V1, where A1 is the area and V1 is the velocity at section 1. Then, use the continuity equation (A1 * V1 = A2 * V2) to find the velocity at other sections of the pipe, such as section 2 and section 3.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

MekFlu #2: Persamaan Bernoulli, Kontinuitas dan Kekekalan Energi

MekFlu #1: Prinsip Persamaan Bernoulli

LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 3
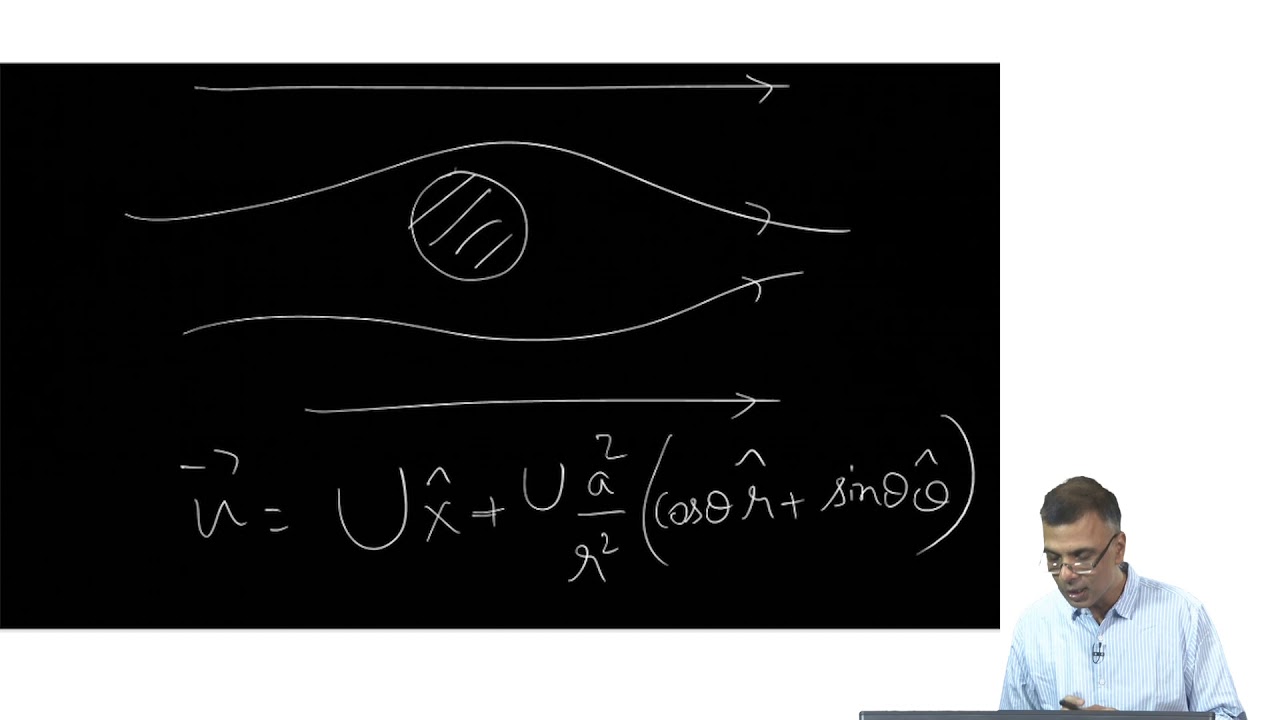
mod03lec11 - Recap - Potential flows, Bernoulli constant and its applications

Fluida Dinamis • Part 1: Fluida Ideal, Debit dan Persamaan Kontinuitas
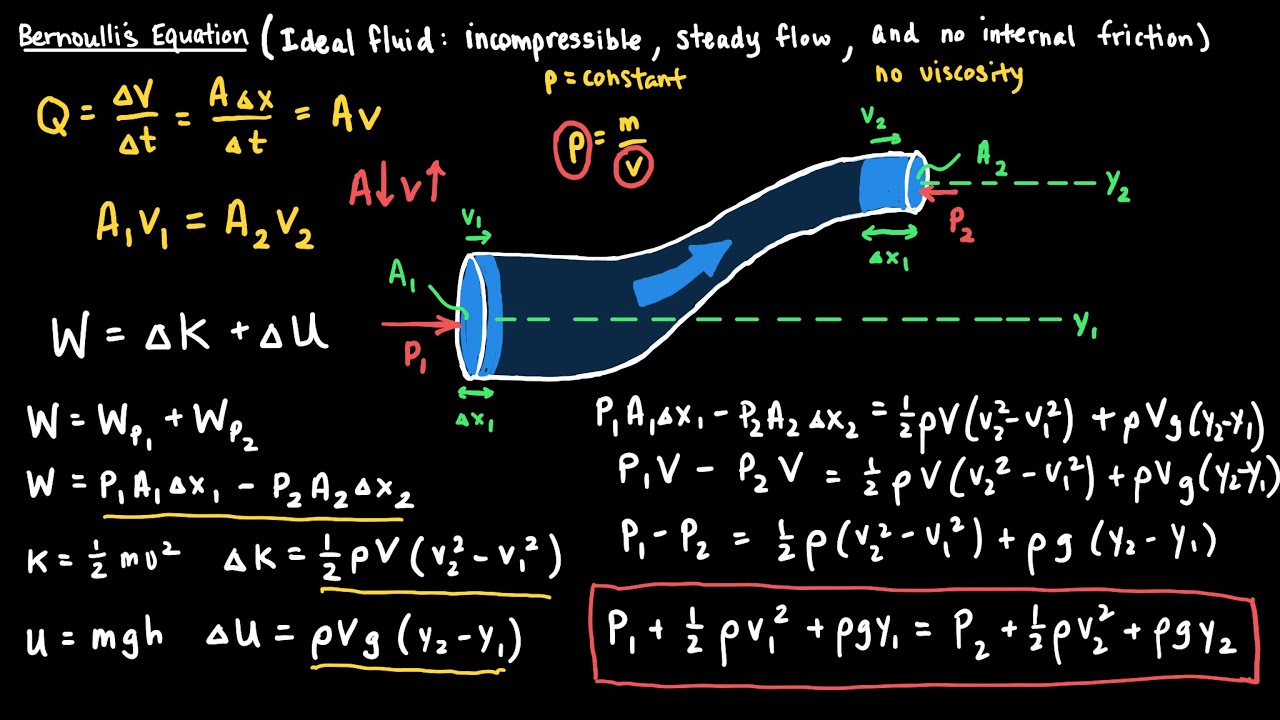
Bernoulli's Equation for Fluid Flow Video in Physics
5.0 / 5 (0 votes)
