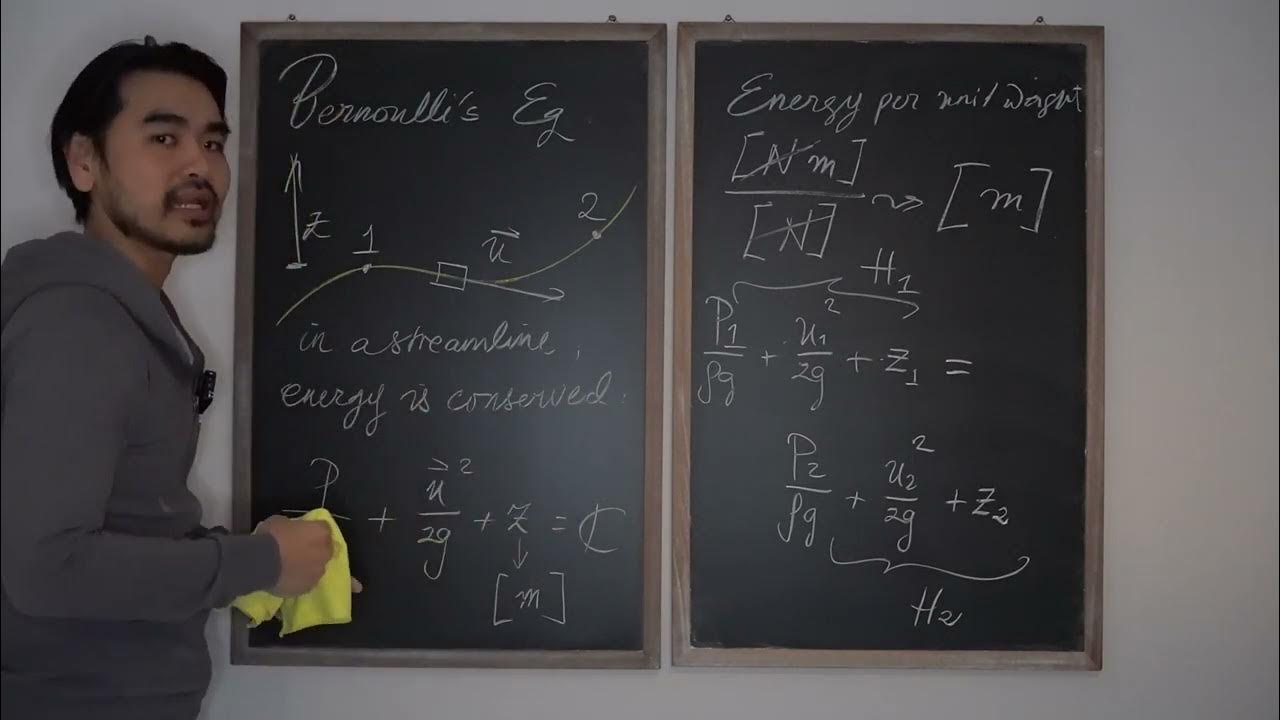mod03lec11 - Recap - Potential flows, Bernoulli constant and its applications

Summary

This video provides an in-depth exploration of fluid dynamics, beginning with a review of streamlines, Bernoulli's principle, and vorticity, before delving into the concepts of circulation and the Magnus effect. The lecturer explains the mathematical formulation of incompressible, inviscid, and irrotational flow, highlighting key equations like the Euler equation and the Bernoulli constant. It also discusses how these concepts apply to practical scenarios such as the flow around a sphere and an airfoil, before concluding with Kelvin's vorticity theorem and the conservation of circulation in inviscid flows. The focus is on fundamental principles and their real-world applications in fluid mechanics.

Takeaways

• 😀 The Navier-Stokes equation was introduced as the focus of the lecture, with a prelude explaining concepts such as streamlines, Bernoulli constant, and vorticity.
• 😀 The lecture begins with a recap of fundamental fluid mechanics concepts, including irrotational, incompressible, and inviscid flow assumptions.
• 😀 In 2D flows, velocity can be expressed as the gradient of a velocity potential or the curl of a stream function, both of which satisfy the Laplace equation.
• 😀 The velocity potential and stream function are orthogonal, similar to electrostatics, and can be treated as components of a single complex variable in the context of fluid dynamics.
• 😀 The solution for the velocity streamlines around a smooth sphere in an inviscid flow is derived using polar coordinates, emphasizing the importance of boundary conditions in solving fluid dynamics problems.
• 😀 The Bernoulli constant was introduced as an energy equation derived from the Euler equation, which relates pressure, velocity, and gravitational potential in inviscid fluids.
• 😀 The Bernoulli constant is conserved along a streamline, which leads to practical applications such as calculating the velocity of fluid flowing out of an orifice and explaining airfoil lift.
• 😀 The velocity of a fluid flowing out of an orifice is given by the formula √(2gh), based on the Bernoulli constant and the assumption that pressure does not vary much between the orifice and the fluid.
• 😀 The concept of airfoil lift is explained through the Bernoulli principle, where the pressure difference between the top and bottom of the airfoil generates an upward force, resulting in lift.
• 😀 Vorticity, which measures rotationality in a fluid flow, was introduced, with an emphasis on its role in inviscid fluids where circulation is conserved, leading to Kelvin's vorticity theorem.
• 😀 Kelvin's vorticity theorem states that circulation is conserved in incompressible, inviscid flow, meaning any existing circulation remains constant over time, and circulation cannot be generated or suppressed in such flows.

Q & A

What is the main focus of the discussion in this script?

The main focus is on fluid dynamics, specifically discussing concepts like the Navier-Stokes equation, Bernoulli’s constant, vorticity, circulation, and the Magnus effect. It also touches on the behavior of inviscid, incompressible, and irrotational fluid flow.

What is the significance of the stream function in 2D fluid flow?

In 2D fluid flow, the stream function is used to express velocity as the curl of the stream function. This function is critical because, for irrotational and incompressible flow, it allows the velocity field to be derived easily and helps to simplify the analysis of the flow dynamics.

How do the conditions of irrotationality, incompressibility, and inviscid flow relate to the velocity potential and stream function?

When the conditions of irrotationality, incompressibility, and inviscid flow are met in 2D, both the velocity potential and stream function satisfy Laplace's equation, meaning they are solutions to a scalar potential and are orthogonal to each other. This relationship simplifies fluid flow analysis, making it easier to derive the velocity field.

What is the Bernoulli constant and how is it derived?

The Bernoulli constant is a result of integrating the Euler equation along a streamline. It represents the conservation of mechanical energy (pressure, velocity, and gravitational potential) along a streamline in an inviscid, incompressible flow. It is derived by integrating the Euler equation and applying boundary conditions along the streamline.

What practical application of Bernoulli’s equation is illustrated in the script?

The script illustrates the application of Bernoulli’s equation to calculate the velocity of fluid flowing out of an orifice. It uses the principle that the Bernoulli constant is conserved along a streamline and assumes the pressure difference across the orifice is negligible.

How does the Bernoulli constant explain the lift generated by an airplane wing?

The Bernoulli constant explains lift generation by showing that if the velocity of air is faster over the top surface of an airfoil than over the bottom, the pressure will be lower on top and higher on the bottom. This pressure difference results in a net upward force, creating lift.

What is vorticity, and how does it relate to fluid flow?

Vorticity is the curl of the velocity field and measures the local rotational motion of fluid particles. In incompressible, inviscid fluids, vorticity is closely tied to the dynamics of the flow, and it plays a key role in understanding rotational flow and circulation.

What is circulation, and how is it conserved in an inviscid flow?

Circulation is a measure of the total rotational motion in a flow, defined as the line integral of the velocity around a closed loop. In an inviscid flow, circulation is conserved, meaning if there is an initial circulation in the flow, it remains constant over time, as there is no viscosity to alter the rotational behavior.

What is Kelvin's vorticity theorem and how does it relate to circulation?

Kelvin's vorticity theorem states that in an incompressible, inviscid flow, the circulation around any closed loop remains constant over time. This theorem emphasizes the conservation of circulation in the absence of viscosity, meaning that vorticity does not dissipate in such flows.

Why is the Magnus effect important, and how is it introduced in the script?

The Magnus effect refers to the phenomenon where a rotating object in a fluid generates a lift force perpendicular to the direction of motion. The script briefly mentions it as a topic to be explored after discussing circulation and conservation of vorticity, indicating its relevance to rotational flows in fluid dynamics.