MekFlu #2: Persamaan Bernoulli, Kontinuitas dan Kekekalan Energi
Summary
TLDRThis video explores key concepts in fluid mechanics, focusing on Bernoulli's equation and the continuity equation. The host revisits the fundamental principles of fluid dynamics, emphasizing the conservation of energy and mass flow. The discussion includes the derivation of Bernoulli’s equation through Newton's second law, the principle of mass conservation leading to the continuity equation, and how these principles are applied to fluid flow in pipes. The session concludes with a practical approach to solving fluid mechanics problems, encouraging further practice with these essential equations.
Takeaways
- 😀 The lesson continues the discussion of fluid mechanics, specifically focusing on Bernoulli's equation and the continuity equation.
- 😀 The continuity equation expresses the conservation of mass in an incompressible fluid, stating that the mass flow rate remains constant along a streamline.
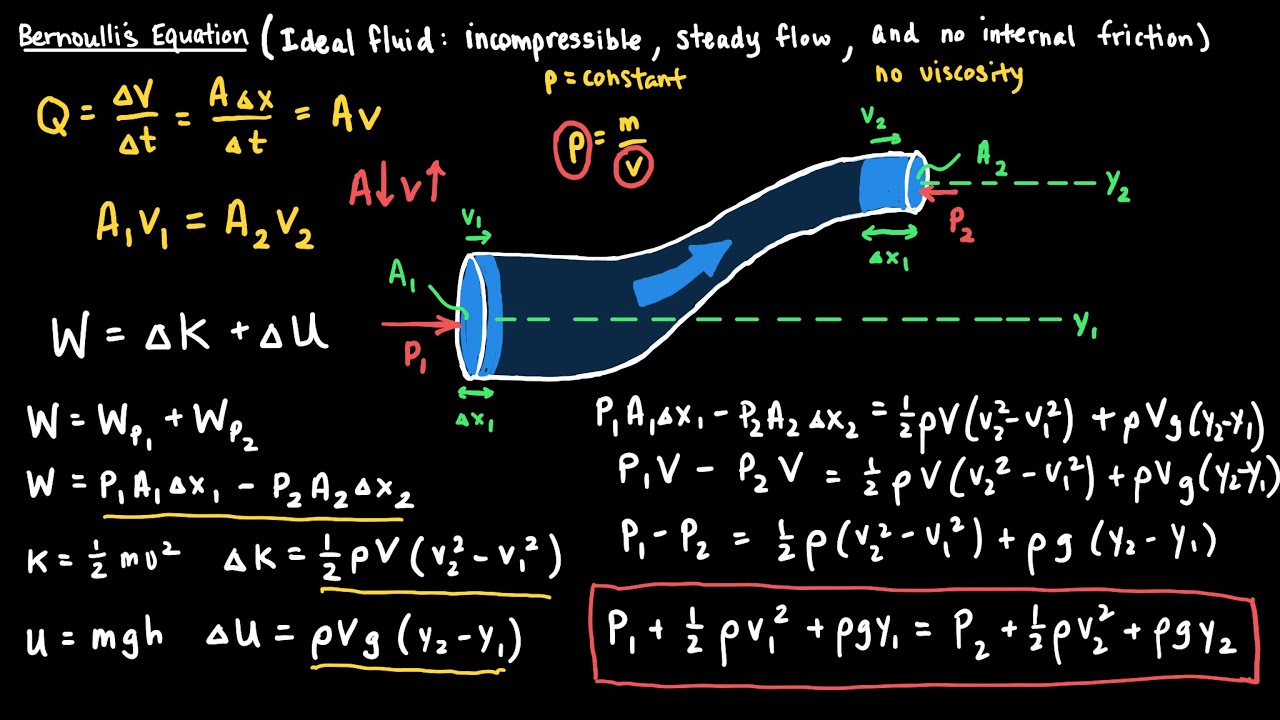
- 😀 Bernoulli's equation is derived from the conservation of energy and Newton's second law, linking pressure, velocity, and height at two points in a fluid.
- 😀 The continuity equation is mathematically expressed as A1V1 = A2V2, showing that a decrease in pipe area leads to an increase in fluid velocity.
- 😀 Bernoulli’s equation is written as P1 + (1/2)ρV1² + ρgh1 = P2 + (1/2)ρV2² + ρgh2, incorporating pressure, velocity, and elevation.
- 😀 The derivation of Bernoulli’s equation involves understanding how forces act on a fluid and how work and energy concepts apply in fluid dynamics.
- 😀 In Bernoulli's equation, if velocity increases, pressure decreases, and vice versa, reflecting the trade-off between kinetic energy and potential energy in a fluid system.
- 😀 The lesson emphasizes the importance of the continuity and Bernoulli equations in understanding fluid behavior in pipes, including changes in velocity and pressure.
- 😀 The principle of conservation of energy is central to both the continuity and Bernoulli equations, explaining how energy is transferred within a flowing fluid.
- 😀 The script prepares the reader for future exercises and problem-solving using Bernoulli’s equation and the continuity equation in practical fluid mechanics scenarios.
Q & A
What is the continuity equation in fluid mechanics?
-The continuity equation in fluid mechanics expresses the conservation of mass in an incompressible fluid. It states that the mass flow rate remains constant, and is represented by the equation: A1 * V1 = A2 * V2, where A is the cross-sectional area and V is the velocity of the fluid.
How does the continuity equation apply to fluid flow in a pipe?
-In a pipe, if the cross-sectional area narrows, the velocity of the fluid increases to maintain a constant mass flow rate, and vice versa. This relationship is described by the continuity equation.
What assumptions are made when deriving Bernoulli’s equation?
-When deriving Bernoulli's equation, several assumptions are made, such as steady, incompressible, non-viscous flow with no energy losses due to friction.
What is Bernoulli’s equation used for in fluid mechanics?
-Bernoulli’s equation is used to relate the pressure, velocity, and elevation of a fluid at different points in a flow. It helps calculate various parameters like pressure differences, velocity changes, and fluid elevation changes.
How is energy conservation related to Bernoulli’s equation?
-Bernoulli's equation is derived from the conservation of mechanical energy. It balances the kinetic energy, potential energy, and pressure energy of a fluid flowing along a streamline.
How is Bernoulli’s equation derived using work-energy principles?
-Bernoulli’s equation can be derived by considering the work done by pressure forces as the fluid moves between two points. This work is related to changes in the fluid’s kinetic and potential energy.
What is the formula for Bernoulli’s equation?
-The formula for Bernoulli’s equation is: P1 + ½ρV1² + ρgH1 = P2 + ½ρV2² + ρgH2, where P is pressure, ρ is density, V is velocity, g is gravitational acceleration, and H is height.
What does the term ‘ρ’ represent in Bernoulli’s equation?
-In Bernoulli’s equation, 'ρ' represents the density of the fluid. It is a measure of the mass per unit volume of the fluid.
What is the significance of the pressure term in Bernoulli’s equation?
-The pressure term in Bernoulli's equation represents the energy stored due to the fluid’s pressure. It balances with the kinetic and potential energy terms as the fluid moves through the system.
How can Bernoulli’s equation be applied to practical fluid flow problems?
-Bernoulli’s equation can be applied to practical fluid flow problems such as calculating the velocity of a fluid at different points in a pipe, determining the pressure differences, or analyzing fluid flow in systems like turbines or venturi tubes.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Dinamika Fluida

Mekanika Fluida FM01 (Lecture3: 8/8). Energy Line & Hydraulic Grade Line

P bahri
Bernoulli's Equation for Fluid Flow Video in Physics

Persamaan Kontinuitas | Bunyi, Rumus dan Penerapan Persamaan Kontinuitas | Fluida Dinamis Kelas 11
Mekanika Fluida FM01 (Lecture3: 1/8). Persamaan Bernoulli (Pengenalan)
5.0 / 5 (0 votes)