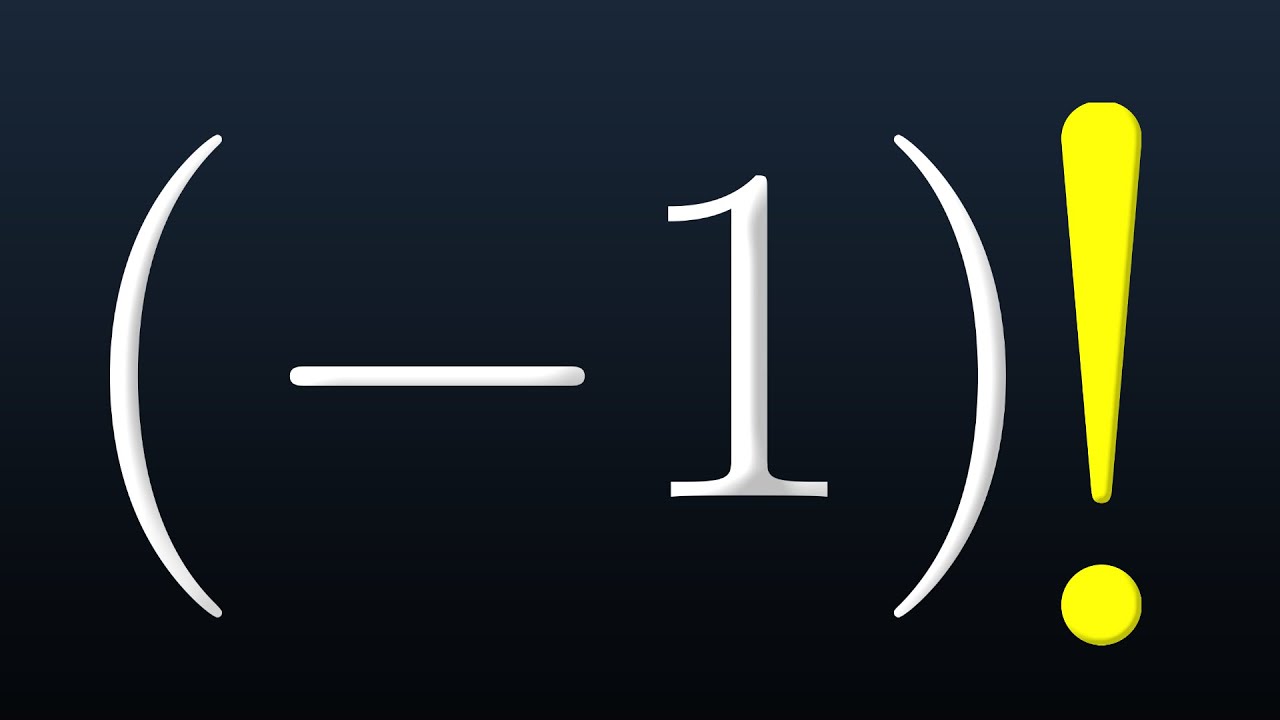7 factorials you probably didn't know
Summary
TLDRIn this video, the host introduces a series of advanced factorials, starting with the familiar regular factorial and diving into more complex types. These include the double factorial, subfactorial (derangement), prime morial, super factorial (with two definitions), exponential factorial, and the hyper factorial. Each type is explained with examples, formulas, and practical applications, especially in areas like combinatorics, number theory, and calculus. The video aims to spark curiosity in mathematical concepts that extend beyond basic factorials, showcasing their intricate properties and uses in problem-solving.
Takeaways
- 😀 Factorials are mathematical expressions that involve multiplying a number by all positive integers smaller than it. For example, 4! = 4 x 3 x 2 x 1.
- 😀 A double factorial (n!!) involves multiplying a number by every second number below it. For example, 4!! = 4 x 2 = 8.
- 😀 The triple factorial (n!!!) is an extension of the double factorial, involving further levels of iteration, but is not commonly used.
- 😀 Subfactorial (!n) refers to the number of derangements, or arrangements where no object appears in its original position. It's calculated using a series of factorials with alternating signs.
- 😀 The prime morial (n#) involves multiplying all prime numbers less than or equal to n. For example, 4# = 3 x 2 = 6.
- 😀 Super factorial (SF) involves multiplying all the factorials from 1 to n. For example, SF(4) = 4! x 3! x 2! x 1!.
- 😀 There's a second definition of super factorial, involving an exponential process where n! is iterated to the power of itself multiple times.
- 😀 Exponential factorial (n$) involves taking the number n and raising it to a series of decreasing powers (n, n-1, n-2, etc.), creating a power tower.
- 😀 Hyper factorial (H(n)) raises each decreasing number starting from n to the power of itself, e.g., H(4) = 4^4 x 3^3 x 2^2 x 1^1.
- 😀 These advanced factorial concepts have applications in various areas of mathematics, particularly in combinatorics, calculus, and number theory.
Q & A
What is a regular factorial and how is it calculated?
-A regular factorial, denoted by n!, is the product of all positive integers up to n. For example, 4! = 4 × 3 × 2 × 1 = 24.
What is a double factorial and how is it different from a regular factorial?
-A double factorial, denoted by n!!, involves multiplying all even numbers (for even n) or all odd numbers (for odd n) from n down to 1. For example, 4!! = 4 × 2 = 8, while 5!! = 5 × 3 × 1 = 15.
What happens when we add a triple factorial (n!!!) or higher factorials?
-Triple factorials and higher factorials are extensions of the factorial concept but are not commonly used in practical applications. They simply continue the pattern of applying more factorial operations.
What is a subfactorial and in what contexts is it used?
-A subfactorial, denoted by !n, is used in combinatorics, particularly to calculate derangements, which are permutations where no item appears in its original position. The formula involves alternating factorial terms and is often applied in discrete mathematics.
How is a subfactorial calculated?
-A subfactorial is calculated by taking n!, then subtracting and adding terms in an alternating series: !n = n! × (1 - 1/1! + 1/2! - 1/3! + ... + (-1)^n/n!). For example, !4 = 9.
What is a prime-morial and how is it calculated?
-A prime-morial, denoted by n#, involves multiplying all prime numbers less than or equal to n. For example, 4# = 3 × 2 = 6, and 7# = 7 × 5 × 3 × 2 = 210.
What is the challenge presented regarding the prime-morial of 1?
-The challenge is to define 1# because 1 is not a prime number. This leads to a question about whether 1# should be 0 or 1.
What is a super factorial and how is it different from a regular factorial?
-A super factorial, denoted by sf(n), involves multiplying all factorials from 1 to n. For example, sf(4) = 4! × 3! × 2! × 1! = 48. Another definition involves exponentiating the factorial of n repeatedly, creating an extremely large number.
How do you calculate the super factorial based on the alternate definition using exponentiation?
-In the alternate definition, the super factorial of n is calculated by taking n! as the base and raising it to the power of itself repeatedly. For example, sf(4) = 24^24, which results in an extremely large number.
What is the hyper factorial, and how is it calculated?
-A hyper factorial, denoted by h(n), involves multiplying powers of integers from n down to 1. For example, h(4) = 4^4 × 3^3 × 2^2 × 1^1 = 27648. It is similar to the super factorial but involves exponentiation instead of multiplication.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)