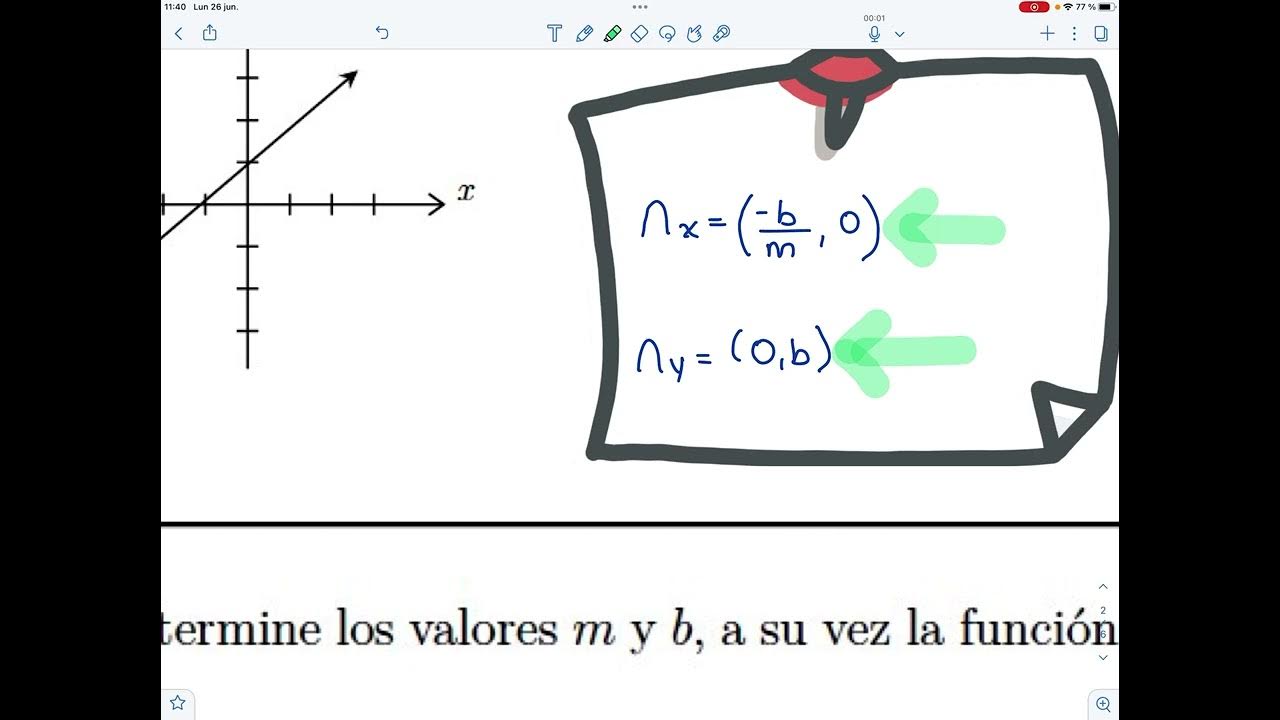
LA FUNCION MEXICO FUNCION MULTIVERSO
Summary
TLDREn este video, se presenta la función México, también conocida como función M o función de PIB. Se explica cómo esta función genera el número Pi, visualizándose como una curva que recuerda la letra 'M'. A través de un análisis que involucra integrales y la validación con una elipse y un círculo, se demuestra que el valor de Pi se aproxima a 3.11, obteniendo un resultado periódico. El objetivo es destacar la importancia de esta función en la demostración matemática y su relación con el valor de Pi, brindando un enfoque interesante y visual sobre el tema.
Takeaways
- 😀 La función México, también conocida como la función M o función de PIB, tiene como característica principal ser un generador del número pi.
- 😀 La curva de la función se asemeja a la letra 'M', lo que le da el nombre de función M o función México.
- 😀 En la representación gráfica de la función, se observa que la curva va de menos 3 hacia valores positivos, formando una 'M'.
- 😀 El radio de la función debe ser siempre positivo, y su intervalo va de 0 a infinito.
- 😀 Debido a que el radio es mayor que cero, la función se representa en el primer cuadrante del plano cartesiano.
- 😀 Para calcular el área de la función, se utilizan integrales simples, lo que permite obtener el valor deseado.
- 😀 A través del proceso de integración, se llega al resultado de 28/9, que es aproximadamente 3.11.
- 😀 El valor obtenido de 28/9 se valida como una aproximación del valor de pi.
- 😀 Además de la función México, el valor de pi se valida utilizando otras formas geométricas, como elipse y círculo.
- 😀 La función México es un ejemplo interesante de cómo se puede aproximar el valor de pi utilizando funciones matemáticas complejas.
- 😀 La periodicidad del valor obtenido (3.11) hace que el resultado sea relevante y útil para entender la función en su totalidad.
Q & A
¿Qué es la Función México o Función M?
-La Función México, también conocida como Función M o Función de PIB, es una función matemática que se utiliza para generar el valor de Pi (π).
¿Por qué se llama Función México o Función M?
-Se le llama Función México o Función M porque su gráfica tiene una forma que se asemeja a la letra 'M', lo que también hace referencia a la forma visual de la función.
¿Cómo se describe la gráfica de la Función México?
-La gráfica de la Función México tiene una curva que va desde valores negativos (como -3) hasta valores positivos, formando una figura que recuerda la letra 'M'.
¿Por qué el radio de la Función México debe ser positivo?
-El radio debe ser positivo porque, según la función, el radio debe estar en el intervalo de cero a infinito, lo que implica que siempre es mayor que cero.
¿Qué relación tiene la Función México con el número Pi?
-La Función México es utilizada para aproximar el valor de Pi mediante el cálculo de áreas utilizando integrales, lo que permite validar el valor de Pi.
¿Qué método matemático se usa para obtener el valor de Pi a partir de la Función México?
-Se utiliza el cálculo de integrales, específicamente integrales sencillas, para obtener el valor aproximado de Pi a partir de la Función México.
¿Cuál es el valor de Pi que se obtiene a través de la Función México?
-El valor obtenido es aproximadamente 28/9, lo que equivale a 3.1111, un valor periódico que se aproxima a Pi.
¿Qué otros métodos se mencionan para validar el valor de Pi?
-Además de la Función México, se menciona que el valor de Pi también ha sido validado utilizando una elipse y un círculo.
¿Por qué es importante la Función México en el estudio del número Pi?
-La Función México es importante porque proporciona una forma alternativa y visual de generar y validar el valor de Pi, destacando su relevancia en las matemáticas.
¿Qué características hacen que la Función México sea interesante en el contexto matemático?
-Lo interesante de la Función México es que permite obtener un valor aproximado de Pi mediante una forma geométrica visual, lo que la convierte en un enfoque original y educativo para el estudio de Pi.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)