1 Funcion lineal
Summary
TLDREl guión ofrece una introducción a las funciones lineales, explicando su definición y características fundamentales. Define la función lineal como 'f(x) = mx + b', donde 'm' es la pendiente y 'b' es el punto de intersección en el eje y. Se discute cómo calcular la pendiente a partir de dos puntos y cómo determinar si la función es creciente, decreciente o constante. Se ejemplifica con una ecuación de recta para encontrar 'm' y 'b', y se asocia con una función lineal, demostrando el proceso de despeje para identificar los valores correctos de 'm' y 'b'.
Takeaways
- 📚 La función lineal se define como f(x) = mx + b, donde m y b son constantes reales que representan la pendiente y el punto de intersección con el eje y, respectivamente.
- 📈 La pendiente m indica si la función es creciente, decreciente o constante, y su valor nos da información sobre el grado de inclinación de la recta.
- 📍 El valor de b nos dice en qué punto la recta interseca el eje y.
- 🔍 Para calcular la pendiente a partir de dos puntos de la función lineal, se utiliza la fórmula (y2 - y1) / (x2 - x1).
- 📐 La recta asociada a la función lineal tiene la forma y = mx + b, y se puede despejar para encontrar el valor de b.
- 🤔 Al encontrar la intersección con el eje x, se utiliza la fórmula m * 0 + b, lo que nos da el valor de b.
- 🔢 Para determinar el punto de intersección con el eje y, se utiliza la fórmula 0 = mx + b, lo que nos permite encontrar el valor de b.
- 📉 La monotonía de la función (si es creciente, decreciente o constante) se deduce del signo de m.
- 👉 Al resolver ejercicios con rectas, es fundamental asegurarse de que la ecuación esté en la forma y = mx + b para identificar correctamente a m y b.
- 📝 En el ejemplo proporcionado, se muestra cómo despejar una ecuación de recta para encontrar los valores de m y b y, a partir de ellos, la función lineal asociada.
Q & A
¿Qué es una función lineal y cómo se define?
-Una función lineal es una relación matemática que se describe por una recta en el plano cartesiano. Se define como f(x) = mx + b, donde m es la pendiente de la recta y b es el ordenada al origen, ambos son constantes reales.
¿Qué información proporciona la pendiente 'm' de una función lineal?
-La pendiente 'm' indica cuánto varía la función lineal en el eje y por unidad en el eje x. También nos dice si la función es creciente (m > 0), decreciente (m < 0) o constante (m = 0), y el grado de inclinación de la recta con respecto al eje de las abscisas.
¿Cómo se calcula la pendiente 'm' de una función lineal a partir de dos puntos?
-Para calcular la pendiente 'm' a partir de dos puntos (x1, y1) y (x2, y2), se utiliza la fórmula m = (y2 - y1) / (x2 - x1).
¿Cómo se determina el valor de 'b' en una función lineal dada dos puntos y la pendiente?
-Para determinar el valor de 'b', se puede utilizar cualquiera de los dos puntos y la pendiente 'm' en la fórmula b = y - mx, donde (x, y) son las coordenadas del punto dado.
¿Qué significa el valor de 'b' en la función lineal f(x) = mx + b?
-El valor de 'b' representa el punto en el que la recta de la función lineal interseca el eje y, es decir, el valor de la función cuando x = 0.
¿Cómo se determina si una función lineal intersecta el eje x?
-Para determinar si una función lineal intersecta el eje x, se calcula el valor de x cuando y = 0, utilizando la fórmula x = -b/m.
¿Cómo se determina el punto de intersección de una función lineal con el eje y?
-El punto de intersección de una función lineal con el eje y se determina cuando x = 0, lo cual se calcula sustituyendo x = 0 en la función, obteniendo y = b.
¿Qué pasos se deben seguir para determinar m y b si se tiene una ecuación de recta en forma no estándar?
-Primero, se debe expresar la ecuación en la forma estándar y = mx + b. Luego, se despeja y para aislarla, y finalmente se identifican los valores de m y b a partir de la ecuación despejada.
¿Cómo se asocia una recta dada con una función lineal?
-Una recta dada se asocia con una función lineal expresando la recta en la forma f(x) = mx + b, donde m es la pendiente y b es el ordenada al origen.
En el ejemplo dado en el guion, ¿cómo se determinan los valores de m y b para la recta 5y - 25x + 30 = 0?
-Se despeja la y de la ecuación 5y - 25x + 30 = 0 obteniendo y = 5x - 6. Luego, se identifican que m = 5 (la pendiente) y b = -6 (el ordenada al origen).
¿Qué función lineal se asocia con la recta dada en el ejemplo del guion?
-La función lineal asociada con la recta 5y - 25x + 30 = 0, una vez despejada y expresada en forma estándar, es f(x) = 5x - 6.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
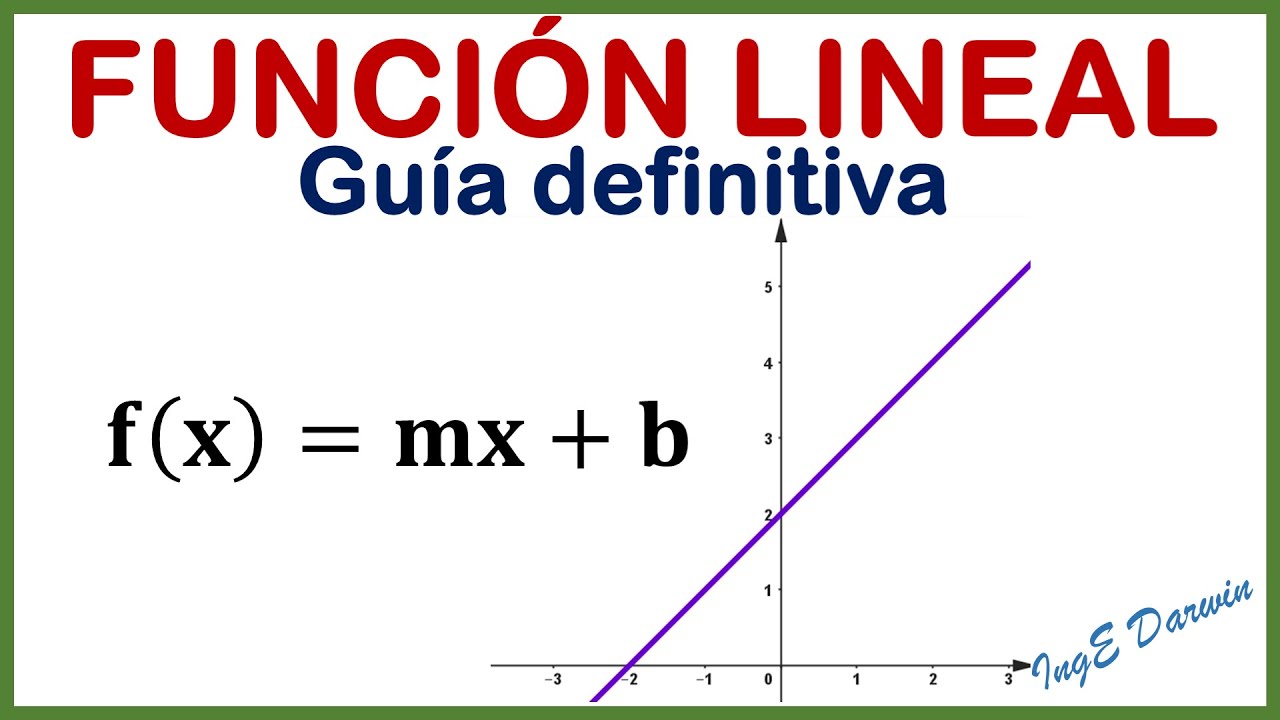
Función Lineal: introducción, características, gráfica, todo lo que necesitas saber | Clase 1

Precálculo, función, dominio y rango

Tipos de funciones
Función Exponencial | Características

Sistema muscular: Tipos, Clasificación, Músculos principales - Anatomía Humana | Kenhub

Polímeros de adición y condensación | Equipo 4.
5.0 / 5 (0 votes)
