Regresión lineal múltiple por MCO (Curso Gretl) #4
Summary
TLDREste video enseña cómo aplicar la regresión lineal múltiple usando Gretel, con un enfoque en cómo varias variables, como el tamaño de terreno, número de baños y la ubicación de una casa, influyen en su precio. A lo largo del tutorial, se exploran los supuestos necesarios para que los estimadores sean confiables y se explica cómo identificar y manejar variables atípicas. Además, se profundiza en la interpretación de los resultados del modelo, destacando la importancia de verificar su ajuste y la significancia de cada variable en el contexto del mercado inmobiliario.
Takeaways
- 😀 La regresión lineal múltiple permite analizar cómo varias variables independientes afectan a una variable dependiente, como el precio de las casas.
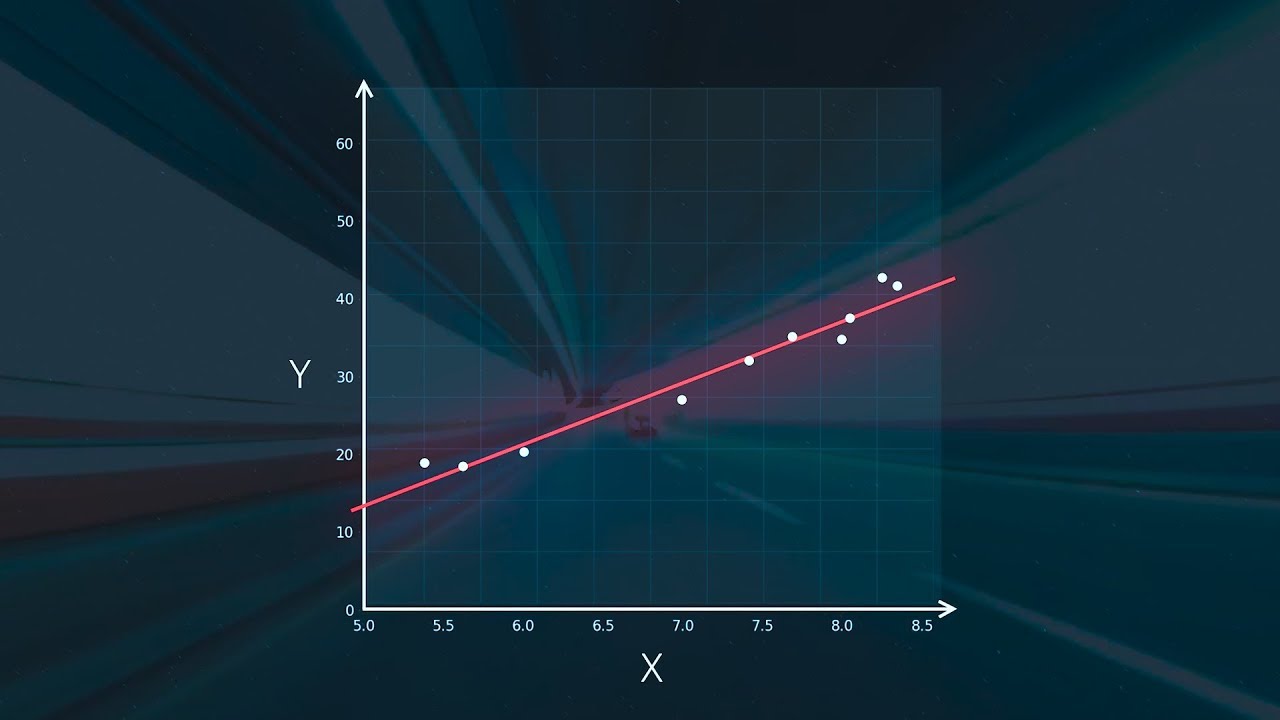
- 😀 Para realizar una regresión lineal múltiple, es fundamental verificar que exista una relación lineal entre las variables, lo cual se puede comprobar con gráficos de dispersión.
- 😀 Los errores en un modelo de regresión deben comportarse de manera aleatoria, sin patrones sistemáticos, y deben tener varianza constante (homoscedasticidad).
- 😀 El modelo de regresión debe cumplir con varios supuestos importantes, como la independencia de los errores y la no correlación entre las variables independientes.
- 😀 La estimación de los coeficientes en una regresión se realiza utilizando el método de los mínimos cuadrados ordinarios (OLS), que busca los mejores estimadores sin sesgo.
- 😀 Es esencial verificar la significancia de los coeficientes de las variables independientes mediante el valor p. Si el valor p es menor a 0.05, el coeficiente es significativo.
- 😀 Un R-cuadrado alto (como 0.86) indica que el modelo explica bien la variabilidad en la variable dependiente, lo que es una buena señal de ajuste.
- 😀 Los datos atípicos pueden afectar el modelo de regresión, ya que pueden distorsionar la relación entre las variables y llevar a estimaciones incorrectas.
- 😀 En el análisis de precios de casas, las variables como el tamaño del terreno, el número de baños y los estacionamientos tienen una relación positiva significativa con el precio.
- 😀 Algunas variables, como la edad de la casa y el número de recámaras, pueden no ser significativas o tener relaciones inesperadas (como un signo negativo en la edad de la casa).
- 😀 Antes de finalizar el análisis, es crucial realizar pruebas de diagnóstico para verificar que los supuestos del modelo de regresión se cumplan adecuadamente y que los resultados sean confiables.
Q & A
¿Qué es la regresión lineal múltiple y por qué es importante en el análisis de datos?
-La regresión lineal múltiple es una técnica estadística utilizada para analizar la relación entre una variable dependiente y varias variables independientes. Es importante porque permite entender cómo múltiples factores afectan una variable de interés, como en el caso de los precios de las casas, donde influyen variables como el tamaño, número de baños y la edad de la casa.
¿Cuál es la diferencia entre regresión lineal simple y regresión lineal múltiple?
-La regresión lineal simple analiza la relación entre dos variables, mientras que la regresión lineal múltiple involucra más de una variable independiente, lo que permite un análisis más complejo y realista de situaciones multifactoriales.
¿Qué significa que los estimadores sean 'lineales e insesgados'?
-Que los estimadores son lineales significa que se basan en combinaciones lineales de las variables independientes. Ser insesgado implica que el valor esperado de los estimadores es igual al valor real del parámetro que se está estimando, lo que asegura que las estimaciones no están sistemáticamente desviadas.
¿Qué tipo de error se incluye en el modelo de regresión y qué función cumple?
-El error en el modelo de regresión es aleatorio y representa las variaciones no explicadas por las variables independientes. Este error es esencial para capturar la variabilidad de los datos que no se puede predecir con el modelo.
¿Por qué es relevante revisar los supuestos de la regresión lineal múltiple?
-Revisar los supuestos es crucial para asegurar que los resultados del modelo sean confiables. Si los supuestos no se cumplen, los estimadores pueden ser sesgados o ineficaces, lo que podría llevar a conclusiones incorrectas.
¿Cuáles son los supuestos más importantes que deben cumplirse en la regresión lineal múltiple?
-Los supuestos clave incluyen: una relación lineal entre las variables, errores que se distribuyen normalmente, independencia de las variables independientes, homoscedasticidad (varianza constante de los errores) e independencia entre los errores a lo largo del tiempo.
¿Cómo se evalúa la significancia de las variables en un modelo de regresión?
-La significancia de las variables se evalúa mediante el valor p de cada coeficiente. Si el valor p es menor que un umbral determinado (usualmente 0.05), se rechaza la hipótesis nula y se concluye que la variable tiene una influencia significativa sobre la variable dependiente.
¿Qué significa un valor p menor que 0.05 en una regresión lineal?
-Un valor p menor que 0.05 indica que existe suficiente evidencia para rechazar la hipótesis nula, lo que significa que el coeficiente de esa variable es significativamente diferente de cero y tiene un impacto relevante sobre la variable dependiente.
¿Cómo afecta el número de baños al precio de una casa según el análisis?
-Según el análisis, cada baño adicional aumenta el precio de la casa en promedio en 2,581 pesos, lo que indica que los baños son una característica valiosa para el mercado inmobiliario.
¿Por qué algunas variables, como la edad de la casa, no son significativas en el modelo?
-Algunas variables, como la edad de la casa, pueden no ser significativas si no tienen una relación clara con la variable dependiente (precio de la casa). En este caso, el análisis muestra que no existe una relación lineal fuerte entre la edad de la casa y su precio.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Pruebas de Multicolinealidad (Curso Gretl) #6

Regresión lineal múltiple en SPSS

REGRESIÓN LINEAL MÚLTIPLE FACIL | SPSS | SUPUESTOS, CUÁNDO Y CÓMO USARLA (JERÁRQUICA, POR PASOS)
Regresión Lineal y Mínimos Cuadrados Ordinarios | DotCSV
16. Modelo de Regresión lineal | Curso de SPSS 29

Coeficiente de Correlación
5.0 / 5 (0 votes)
