REGRESIÓN LINEAL MÚLTIPLE FACIL | SPSS | SUPUESTOS, CUÁNDO Y CÓMO USARLA (JERÁRQUICA, POR PASOS)

Psico Facil

10 Sept 201910:00

Summary

TLDREn este episodio de 'Psico Fácil', Javier introduce la regresión lineal múltiple, una técnica estadística utilizada para determinar cómo múltiples variables predictoras influyen en una variable de interés. Se explica que, a diferencia de la regresión lineal simple, esta técnica permite incluir varios factores que pueden afectar el resultado, como la calidad del producto, el precio, la publicidad y el tipo de país. Javier detalla tres métodos de selección de predictores: jerárquico, por entrada forzada y por pasos, y subraya la importancia de elegir variables teóricamente justificadas. Además, menciona los requisitos para realizar una regresión lineal múltiple, como la ausencia de multicolinealidad y la necesidad de que las variables predictoras sean cuantitativas. Se invita a los espectadores a seguir el canal y a ver más contenido educativo en estadísticas.

Takeaways

📚 Hoy se explora la regresión lineal múltiple, una técnica estadística avanzada para analizar múltiples variables predictoras y su impacto en una variable de interés.
🔍 Se destaca la importancia de comprender que en la vida real, a menudo múltiples factores influyen en los resultados, como en el ejemplo de las ventas de una empresa.
✅ Se explica que la regresión lineal simple es una herramienta básica, pero la regresión lineal múltiple es necesaria para modelos más complejos.
📈 Se menciona que la ecuación de regresión se complica con el aumento de variables predictoras, lo que requiere un análisis más detallado.
🧐 Se enfatiza la necesidad de ser cuidadosos al seleccionar variables para el análisis, ya que esto afecta directamente a los coeficientes de regresión.
🔬 Se presenta la idea de que las variables predictoras deben ser teóricamente justificadas y no añadidas al azar al modelo.
📊 Se describen tres métodos principales de regresión lineal múltiple: jerárquico, por entrada forzada y por pasos, cada uno con sus propios usos y ventajas.
📝 Se resalta la importancia de la selección de predictores, ya que el orden de inclusión puede afectar significativamente a los resultados del modelo.
📐 Se mencionan los requisitos para realizar una regresión lineal múltiple, incluyendo la necesidad de que las variables predictoras sean cuantitativas y no estén altamente correlacionadas entre sí (sin multicolinealidad).
💻 Se sugiere que para realizar análisis estadísticos avanzados, se debe usar software estadístico específico, como SPSS, y se invita a los espectadores a ver futuras explicaciones en videos subsecuentes.

Q & A

¿Qué es la regresión lineal múltiple y cómo se diferencia de la regresión lineal simple?
-La regresión lineal múltiple es un método estadístico que permite predecir una variable de interés (variable criterio) a partir de dos o más variables predictoras. Se diferencia de la regresión lineal simple en que esta última solo utiliza una variable predictora para predecir la variable de interés.
¿Cuál es el propósito de utilizar múltiples variables predictoras en un modelo de regresión lineal múltiple?
-El propósito es poder explicar mejor el cambio en la variable de interés, ya que en la realidad, a menudo múltiples factores influyen en un resultado específico, permitiendo así una predicción más precisa y un análisis más profundo de los datos.
¿Cómo se determina la ecuación de regresión lineal múltiple en un ejemplo práctico?
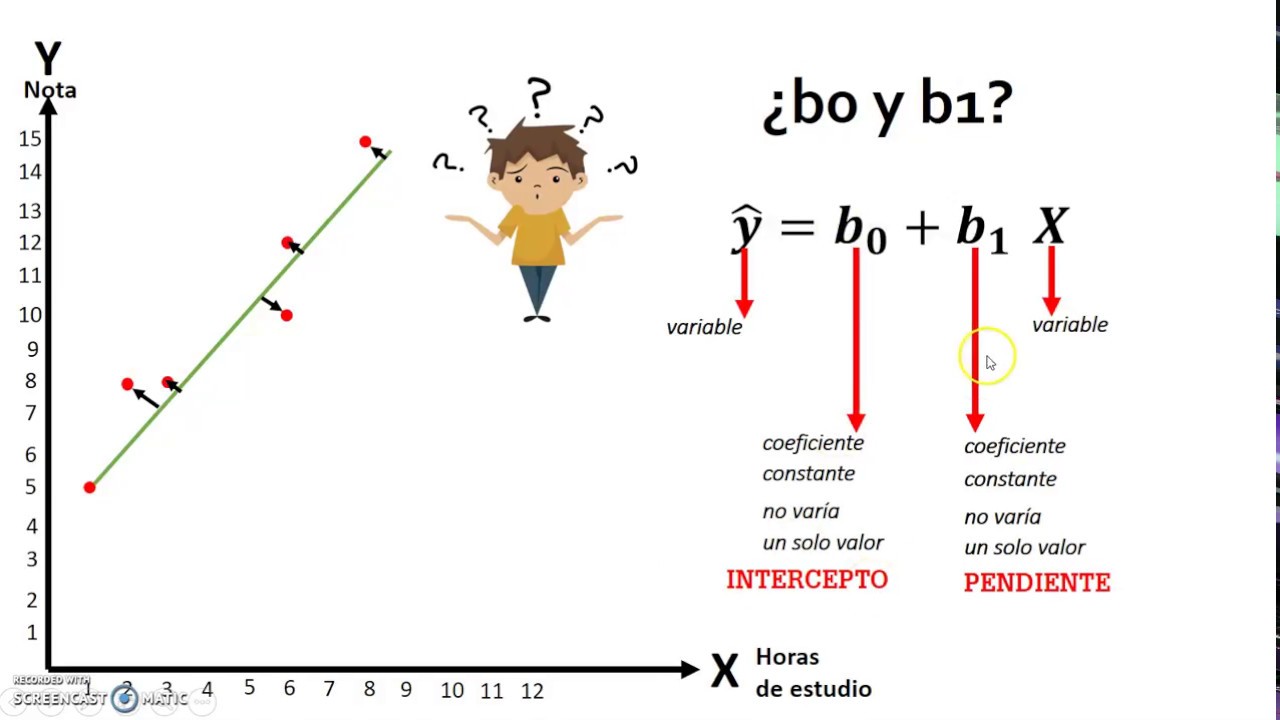
-En un ejemplo práctico, como las ventas de una empresa, la ecuación de regresión lineal múltiple se determina agregando múltiples términos que corresponden a los coeficientes multiplicados por las variables predictoras, como calidad del producto, precio, inversión en publicidad y tipo de país.
¿Qué es el coeficiente de determinación (R²) y cómo se interpreta en el contexto de la regresión lineal múltiple?
-El coeficiente de determinación (R²) es una medida que indica qué porcentaje de la variabilidad de la variable de interés puede ser explicada por la variable predictora. Un valor cercano a 1 indica una buena explicación, mientras que uno cercano a 0 indica que la variable predictora no explica mucho de la variabilidad.
¿Cuál es la importancia de seleccionar adecuadamente las variables predictoras en un modelo de regresión múltiple?
-Es crucial seleccionar las variables predictoras adecuadamente porque el coeficiente de regresión depende de ellas. Las variables seleccionadas deben tener un impacto teórico conocido y ser relevantes para la variable de interés, evitando incluir variables aleatorias que podrían distorsionar los resultados.
¿Qué métodos diferentes existen para realizar una regresión lineal múltiple y cuáles son sus diferencias?
-Existen tres métodos principales: regresión jerárquica, entrada forzada y regresión por pasos. La regresión jerárquica se basa en un orden de importancia teórica, la entrada forzada incluye todas las variables al mismo tiempo y no sigue un orden específico, mientras que la regresión por pasos agrega o elimina variables basándose en criterios matemáticos.
¿Qué es la 'entrada forzada' en el contexto de la regresión lineal múltiple?
-La 'entrada forzada' es un método en el cual todas las variables predictoras se ingresan al modelo de regresión simultáneamente, sin seguir un orden específico, y se basa en aspectos teóricos para incluir los predictores.
¿Cómo se define el método directo en la regresión por pasos?
-El método directo en la regresión por pasos implica comenzar con un modelo que solo contiene la constante y luego ir seleccionando variables que mejor predigan la variable de interés, basándose en la mayor correlación simple o parcial con el resultado.
¿Qué es la 'multicolinealidad' y por qué es importante evitarla en la regresión lineal múltiple?
-La multicolinealidad ocurre cuando las variables predictoras están altamente correlacionadas entre sí. Es importante evitarla porque puede distorsionar los coeficientes estimados, dificultando la interpretación y confiabilidad del modelo.
¿Cuáles son los requisitos básicos que debe cumplir una regresión lineal múltiple antes de realizar el análisis?
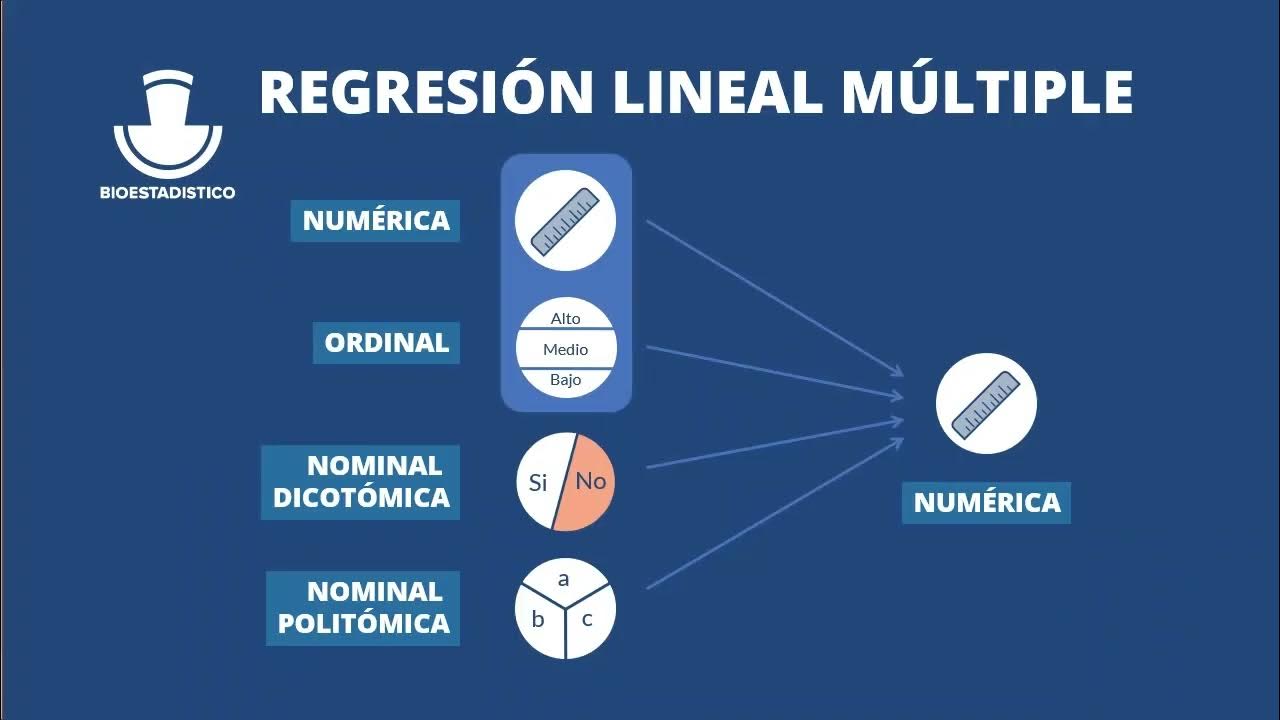
-Los requisitos básicos incluyen que las variables predictoras sean cuantitativas y cualitativas con al menos dos categorías, la variable de interés debe ser cuantitativa de intervalo, las variables predictoras deben tener varianza diferente de 0, no presentar multicolinealidad y no estar correlacionadas con variables externas no incluidas en el modelo.

Outlines

00:00

📊 Introducción a la Regresión Lineal Múltiple

Este primer párrafo introduce el concepto de regresión lineal múltiple, una técnica estadística que permite analizar cómo múltiples variables predictoras influyen en una variable de interés. Se explica que, a diferencia de la regresión lineal simple que solo considera una variable predictora, la regresión múltiple puede incluir múltiples factores que afectan a una variable, como en el ejemplo de las ventas de una empresa que pueden verse influenciadas por la calidad del producto, el precio, la publicidad y las condiciones sociales. Además, se menciona la importancia de seleccionar cuidadosamente las variables para el análisis, ya que el coeficiente de regresión dependerá de ellas y también afectará la forma en que se ingresan en el modelo.

05:01

🔍 Métodos de Selección de Variables en Regresión Lineal Múltiple

El segundo párrafo se enfoca en los diferentes métodos para seleccionar variables en un modelo de regresión lineal múltiple. Se describen tres enfoques principales: el modelo jerárquico, el método de entrada forzada y el método de pasos. El modelo jerárquico se basa en la teoría previa y en el orden de importancia de las variables, mientras que el método de entrada forzada introduce todas las variables al mismo tiempo y no sigue un orden específico. El método de pasos es un proceso iterativo que puede incluir o eliminar variables basándose en su contribución al modelo. Además, se mencionan los requisitos que deben cumplirse para realizar una regresión lineal múltiple, como que las variables predictoras sean cuantitativas y que no haya multicolinealidad, y se sugiere que el análisis se realizará en SPSS, un software estadístico comúnmente utilizado.

Mindmap

Keywords

💡Regresión lineal múltiple

Es una técnica estadística utilizada para modelar la relación entre una variable de interés y múltiples variables predictoras. En el vídeo, se menciona que esta técnica permite entender cómo factores como la calidad del producto, el precio, la publicidad y el tipo de país pueden influir en las ventas de una empresa, más allá de lo que una regresión lineal simple podría explicar.

💡Variable predictora

Las variables predictoras son aquellas que se utilizan para predecir el valor de otra variable, conocida como variable de interés o criterio. En el guion, se da el ejemplo de que la calidad del producto, el precio, la inversión en publicidad y el tipo de país son variables predictoras que influyen en las ganancias de una empresa.

💡Coeficiente de determinación (R²)

El coeficiente de determinación es una medida estadística que indica la cantidad de variabilidad para la variable de interés que puede ser explicada por la regresión. En el vídeo, se sugiere que cada variable predictora aporta a través de su coeficiente a la explicación del cambio en la variable de interés.

💡Selección de variables

Es el proceso de decidir qué variables incluir en un modelo de regresión. En el vídeo se enfatiza la importancia de seleccionar variables predictoras basadas en investigaciones previas y un conocimiento sólido del constructo teórico, como en el ejemplo de no incluir el tipo de leche que consumen las personas como predictora de las ventas de discos musicales.

💡Regresión jerárquica

Este método de regresión múltiple implica ingresar las variables predictoras en un orden específico basado en la teoría o en hallazgos previos. Se menciona en el vídeo que es útil cuando se tiene claridad sobre la importancia relativa de las variables y se desea que las variables ingresen al modelo en un orden que refleje esa importancia.

💡Entrada forzada

Es una técnica en la que todas las variables predictoras se ingresan al modelo de una sola vez, sin un orden específico. En el vídeo, se describe cómo este método se basa en aspectos teóricos para incluir predictores, pero no sigue un orden predeterminado, lo que puede ser útil para pruebas teóricas.

💡Regresión por pasos

Este enfoque implica agregar o eliminar variables del modelo basándose en criterios estadísticos. Se divide en método directo, método hacia atrás y método de paso a paso, donde se evalúan las contribuciones de las variables al modelo y se decide su inclusión o exclusión. En el vídeo, se explica cómo estos métodos ayudan a construir modelos más precisos al seleccionar solo las variables más relevantes.

💡Multicolinealidad

Se refiere a una situación en la que dos o más variables predictoras están altamente correlacionadas entre sí. En el vídeo, se menciona que es importante evitar la multicolinealidad porque puede distorsionar los coeficientes estimados y dificultar la interpretación del modelo.

💡Requisitos de la regresión lineal múltiple

El vídeo detalla los requisitos que deben cumplirse para realizar una regresión lineal múltiple, como que las variables predictoras sean cuantitativas y la variable de interés cuantitativa de intervalo, además de que no presenten multicolinealidad y que no estén correlacionadas con variables externas no incluidas en el modelo.

💡SPSS

SPSS (Statistical Package for the Social Sciences) es un software estadístico utilizado para el análisis de datos. En el vídeo, se sugiere que los análisis de regresión lineal múltiple se realizan en SPSS, lo que indica que este software es una herramienta común para aplicar técnicas de regresión múltiple en la práctica.

Highlights

Introducción al capítulo de regresión lineal múltiple en el canal Psicó Fácil.

Explicación de la regresión lineal simple y su limitación al solo considerar una variable predictora.

Importancia de considerar múltiples variables predictoras para explicar mejor los cambios en una variable de interés.

Ejemplo práctico de cómo varias variables pueden influir en las ventas de una empresa.

Descripción de cómo se construye la ecuación de regresión lineal múltiple con múltiples variables predictoras.

Importancia del coeficiente de determinación (R²) para medir la variabilidad explicada por el modelo.

Necesidad de ser cuidadosos al seleccionar variables para el análisis para no distorsionar los coeficientes de regresión.

Importancia de la teoría y la investigación previa en la selección de variables predictoras.

Comparación entre la regresión lineal múltiple y la simple en términos de inclusión de predictores.

Métodos para seleccionar variables predictoras: Jerárquico, Forzado y Paso a Paso.

Descripción del método de regresión jerárquica y su enfoque en la teoría y el orden de entrada de variables.

Explicación del método de entrada forzada y su inclusión de todas las variables predictoras al mismo tiempo.

Introducción al método de regresión por pasos, incluyendo directo, hacia atrás y hacia adelante.

Descripción del método directo y su enfoque en la selección de predictores por correlación simple y parcial.

Detalles sobre el método de paso a paso y su proceso de agregar y eliminar predictores según su contribución al modelo.

Requisitos básicos que debe cumplir la regresión lineal múltiple para ser válida, incluyendo la calidad de las variables predictoras.

Necesidad de evitar la multicolinealidad y la correlación con variables externas en el modelo de regresión.

Invitación a los espectadores a realizar análisis en SPSS y a ver el próximo vídeo para aprender más.

Oportunidad para que los espectadores hagan preguntas y contribuyan al canal a través de PayPal.

Invitación a suscribirse al canal y seguir en redes sociales para no perderse de futuras publicaciones.