Regresión lineal múltiple en SPSS
Summary
TLDREn este video, Elías Alvarado explica la técnica estadística de la regresión lineal múltiple, utilizada para modelar la relación entre una variable dependiente y varias independientes. Utilizando un ejemplo con trabajadores, describe cómo variables como la edad, el ingreso y el tamaño de la empresa pueden influir en el estrés laboral. Se analiza el proceso de obtener los coeficientes óptimos para el modelo, utilizando herramientas como la correlación, el análisis de varianza (ANOVA) y la selección de variables. Finalmente, se demuestra cómo elegir el modelo más ajustado mediante un método de selección paso a paso.
Takeaways
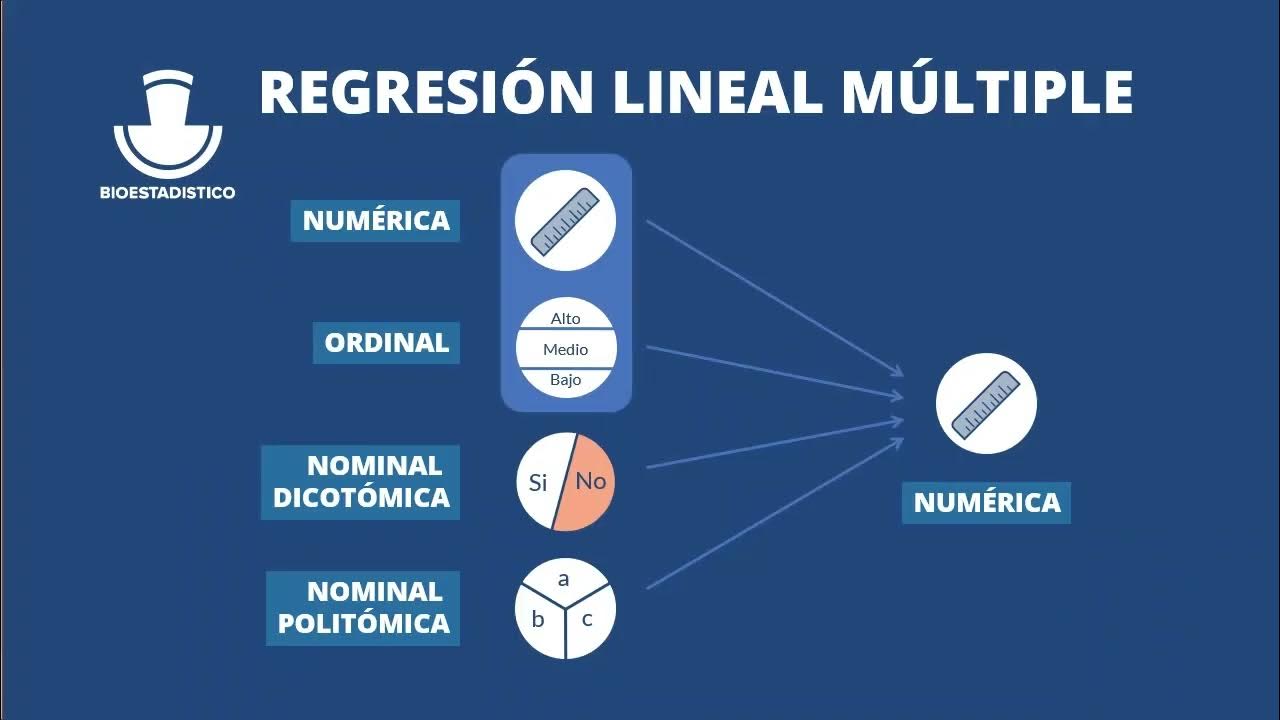
- 😀 La regresión lineal múltiple es una técnica estadística que modela la relación entre una variable dependiente y dos o más variables independientes.
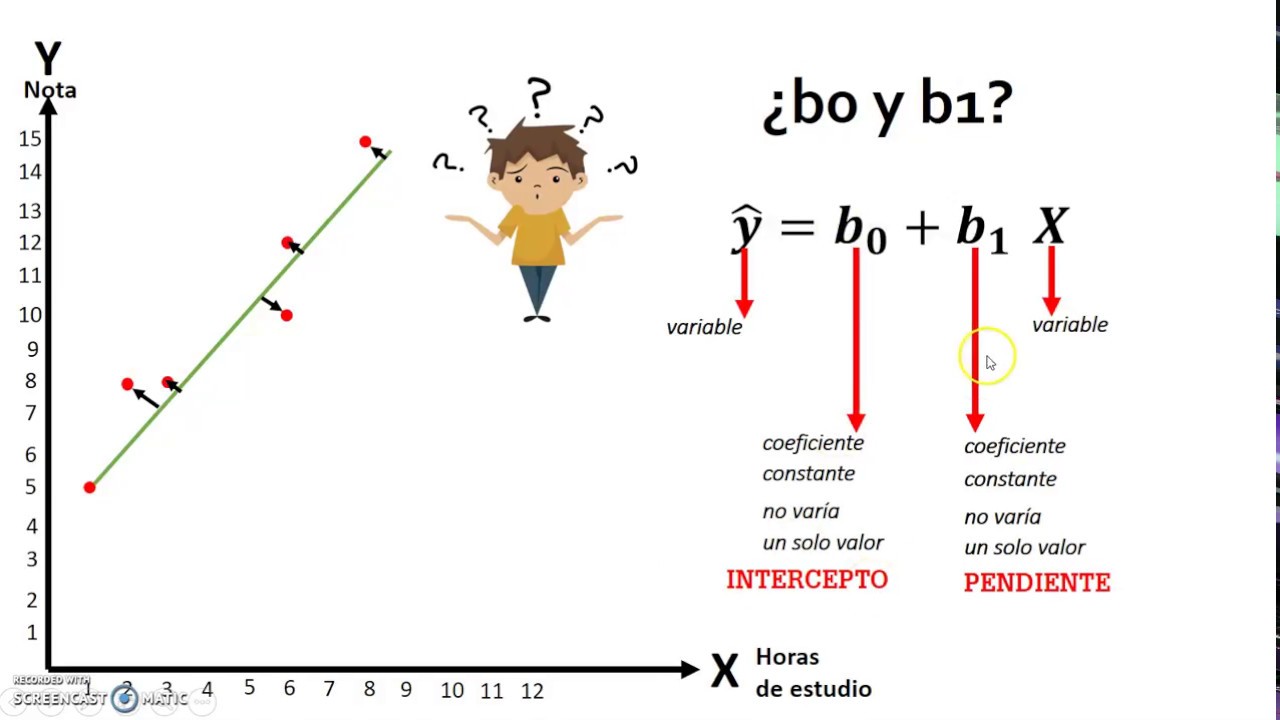
- 😀 La ecuación clásica de la regresión lineal múltiple es: y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε.
- 😀 El objetivo principal de la regresión lineal múltiple es encontrar los valores óptimos de los coeficientes para minimizar la suma de los cuadrados de los residuos.
- 😀 Un ejemplo práctico de regresión lineal múltiple puede ser la predicción del estrés de los empleados, utilizando variables como edad, antigüedad, tamaño de la empresa e ingresos.
- 😀 El coeficiente de correlación (R = 0.918) indica una relación fuerte y positiva entre las variables independientes y el nivel de estrés de los empleados.
- 😀 El R-cuadrado (0.842) sugiere que el 84.2% de la variabilidad en el estrés de los empleados puede ser explicada por las variables seleccionadas.
- 😀 En el análisis de la ANOVA, se rechaza la hipótesis nula, lo que implica que al menos una variable independiente tiene un efecto significativo en el estrés de los empleados.
- 😀 El análisis de los coeficientes muestra que variables como la edad, tamaño de la empresa e ingresos son estadísticamente significativas para predecir el estrés.
- 😀 Un coeficiente positivo, como el del ingreso (0.002), indica una relación positiva entre el ingreso y el estrés, es decir, a mayor ingreso, mayor estrés.
- 😀 El método de selección de variables por pasos (stepwise) permite seleccionar las variables más significativas y eliminar las que no contribuyen al modelo, como en el caso de la antigüedad.
- 😀 Al utilizar el método de selección por pasos, se obtiene un modelo optimizado que incluye solo las variables que mejor explican el estrés en los empleados, como edad, tamaño de la empresa e ingresos.
Q & A
¿Qué es la regresión lineal múltiple?
-La regresión lineal múltiple es una técnica estadística que se utiliza para modelar la relación entre una variable dependiente y dos o más variables independientes. Su objetivo es predecir el valor de la variable dependiente a partir de las independientes.
¿Qué representa la ecuación de regresión lineal múltiple?
-La ecuación de regresión lineal múltiple incluye la variable dependiente (y), las variables independientes (x₁, x₂, ..., xₙ), los coeficientes de regresión (β₁, β₂, ..., βₙ), y el término de error (e) que captura las diferencias entre las predicciones y los valores reales.
¿Cuál es el objetivo principal de la regresión lineal múltiple?
-El objetivo principal es encontrar los valores óptimos de los coeficientes de regresión para minimizar la suma de los cuadrados de los residuos, que son las diferencias entre las predicciones y los valores reales.
¿Cómo se puede interpretar un valor de R² de 0.842?
-Un valor de R² de 0.842 indica que aproximadamente el 84.2% de la variabilidad total de la variable dependiente (en este caso, el estrés) es explicada por las variables independientes utilizadas en el modelo.
¿Qué significa que se rechace la hipótesis nula en la ANOVA?
-Cuando se rechaza la hipótesis nula en la ANOVA, significa que al menos una de las variables independientes tiene un efecto significativo sobre la variable dependiente, lo que indica que el modelo es útil para explicar las variaciones observadas en los datos.
¿Qué variables fueron significativas en el ejemplo proporcionado?
-En el ejemplo, las variables significativas fueron la edad, el tamaño de la empresa y el ingreso, ya que sus coeficientes de t de Student y nivel de significancia cumplían los criterios estadísticos establecidos.
¿Qué implica un coeficiente positivo para una variable independiente?
-Un coeficiente positivo indica una relación directa entre la variable independiente y la dependiente. En el ejemplo, el coeficiente positivo para el ingreso sugiere que un aumento en el ingreso está asociado con un aumento en el estrés.
¿Qué es el método de selección por pasos (escalonado) en la regresión?
-El método de selección por pasos o escalonado es un proceso que permite agregar o eliminar variables independientes en el modelo basándose en su significancia estadística, con el fin de encontrar el mejor modelo ajustado a los datos.
¿Cómo se seleccionan las variables en el método de selección por pasos?
-Las variables se seleccionan agregando o eliminando aquellas que tienen un valor p bajo, lo que indica que son estadísticamente significativas. Este proceso ayuda a identificar las variables que más contribuyen al modelo.
¿Qué diferencia hay entre el primer y el tercer modelo recomendado por el método de selección?
-La diferencia radica en las variables seleccionadas: el tercer modelo es el más óptimo porque incluye solo las variables que son estadísticamente significativas, mientras que el primer modelo incluye variables no significativas como la antigüedad.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)