Puntos críticos, crece y decrece, máximos y mínimos locales, inflexión y concavidad de una función 1
Summary
TLDREn este video se aborda el análisis de funciones, centrándose en aspectos clave como los puntos críticos, intervalos de crecimiento y decrecimiento, así como máximos y mínimos relativos. Se explica el proceso de derivación para identificar estos puntos, junto con la importancia de la segunda derivada para determinar la concavidad y los puntos de inflexión. A lo largo del ejercicio, se combinan análisis algebraicos y gráficos, facilitando una comprensión integral de cómo las funciones se comportan en diferentes intervalos y cómo interpretar estos resultados de manera efectiva.
Takeaways
- 😀 La función se analiza a través de la derivada para encontrar puntos críticos.
- 😀 Los puntos críticos se determinan igualando la primera derivada a cero.
- 😀 Se utiliza una recta numérica para identificar intervalos crecientes y decrecientes.
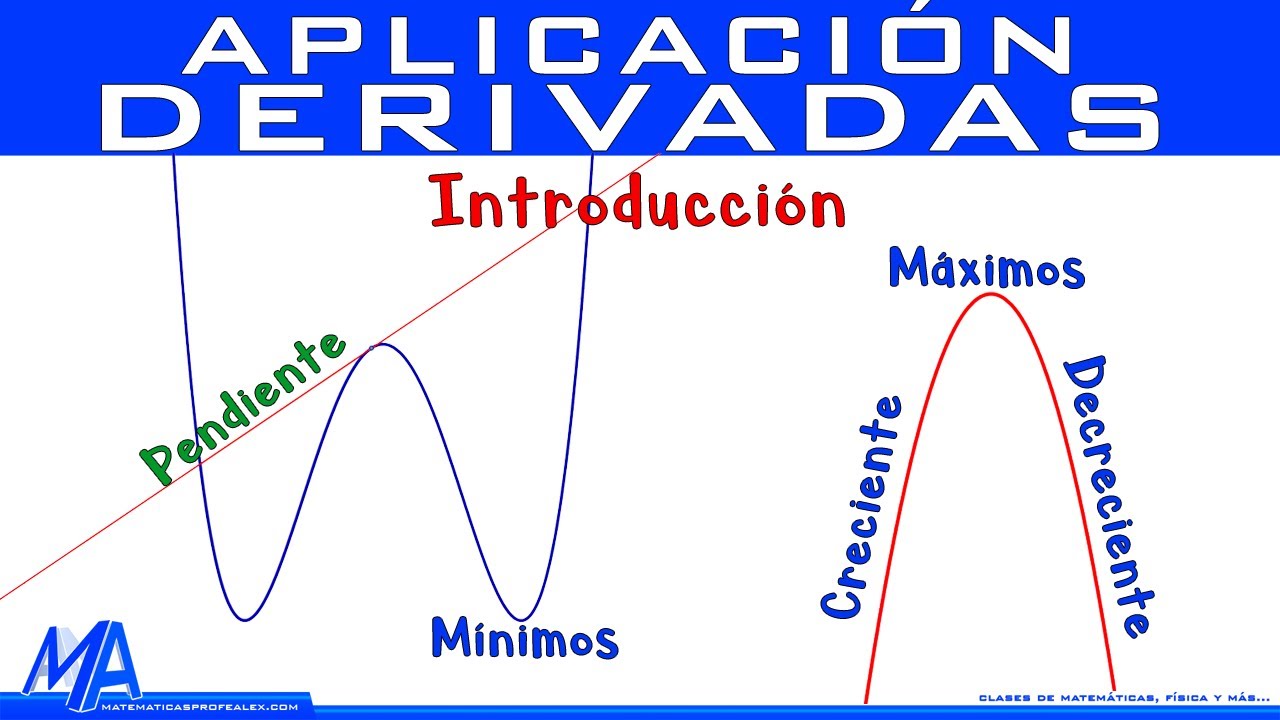
- 😀 La función es creciente donde la primera derivada es positiva y decreciente donde es negativa.
- 😀 Un cambio de la primera derivada de positivo a negativo indica un máximo local.
- 😀 Un cambio de la primera derivada de negativo a positivo indica un mínimo local.
- 😀 Para encontrar puntos de inflexión, se calcula la segunda derivada y se busca su cambio de signo.
- 😀 La concavidad de la función se determina mediante la segunda derivada: positiva indica concavidad hacia arriba y negativa hacia abajo.
- 😀 La representación gráfica de la función ayuda a visualizar los puntos críticos y cambios de concavidad.
- 😀 Se hace hincapié en que los máximos y mínimos locales no son necesariamente los extremos absolutos de la función.
Q & A
¿Qué se pretende analizar en esta serie de vídeos?
-Se pretende analizar funciones, identificando puntos críticos, máximos y mínimos relativos, y puntos de inflexión, además de graficar la función para entender su comportamiento analítico y geométrico.
¿Cuál es el primer paso para determinar los puntos críticos de una función?
-El primer paso es derivar la función y luego igualar la derivada a cero para encontrar los puntos críticos.
¿Cómo se identifica si la función es creciente o decreciente?
-Se localizan los puntos críticos en una recta numérica y se evalúa la primera derivada en intervalos alrededor de esos puntos para determinar el signo (positivo o negativo), lo que indica si la función es creciente o decreciente.
¿Qué indica un cambio de signo en la primera derivada?
-Un cambio de signo de positivo a negativo indica un máximo local, mientras que un cambio de negativo a positivo indica un mínimo local.
¿Cómo se hallan las coordenadas de los máximos y mínimos locales?
-Se sustituyen los puntos críticos en la función original para obtener sus coordenadas (x, y).
¿Cuál es el propósito de calcular la segunda derivada?
-La segunda derivada se calcula para determinar los puntos de inflexión y la concavidad de la función.
¿Qué significa que la función sea cóncava hacia arriba o hacia abajo?
-La función es cóncava hacia abajo cuando la segunda derivada es negativa, y cóncava hacia arriba cuando es positiva.
¿Cómo se determina un punto de inflexión?
-Un punto de inflexión se determina al encontrar donde la segunda derivada cambia de signo.
¿Qué se debe graficar para interpretar los resultados analíticos?
-Se deben graficar los puntos críticos, máximos y mínimos, y los puntos de inflexión para visualizar cómo se comporta la función.
¿Qué diferencia hay entre máximos/mínimos relativos y absolutos?
-Los máximos y mínimos relativos son valores locales en comparación con otros en la vecindad, mientras que los máximos y mínimos absolutos son los valores más altos o bajos de toda la función.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Máximo relativo, mínimo relativo, intervalos de crecimiento y decrecimiento de una función

Funciones.Dominio, recorrido, cortes, continuidad, crecimiento, decrecimiento, máximos, mínimos

04. Maximum, minimum, growth and decrease: criterion of the first derivative

Derivadas Máximos, Mínimos, Crecimientos y Concavidad

ANÁLISIS DE FUNCIONES
Aplicación de la derivada Introducción
5.0 / 5 (0 votes)
