Turunanfungsi Trigonometri Bag 1
Summary
TLDRIn this educational session, the instructor introduces the concept of trigonometric derivatives, focusing on the definition and importance of differentiation in calculus. The lesson includes a detailed explanation of how to find the derivatives of sine and cosine functions, using limits and fundamental trigonometric identities. Examples are provided, such as proving the derivative of sin(x) equals cos(x) and calculating derivatives for composite functions like sin(3x) and cos(2x). The instructor emphasizes the necessity of understanding these concepts to apply them confidently in further mathematical studies, encouraging students to engage actively with the material.
Takeaways
- 😀 Understanding derivatives is crucial as it measures how a function changes with varying input values.
- 📏 The process of finding a derivative is called differentiation.
- 🔄 The reverse process of differentiation is called anti-differentiation, which relates to integration.
- 📊 Trigonometric functions are significant in calculus, and their derivatives can be derived using established formulas.
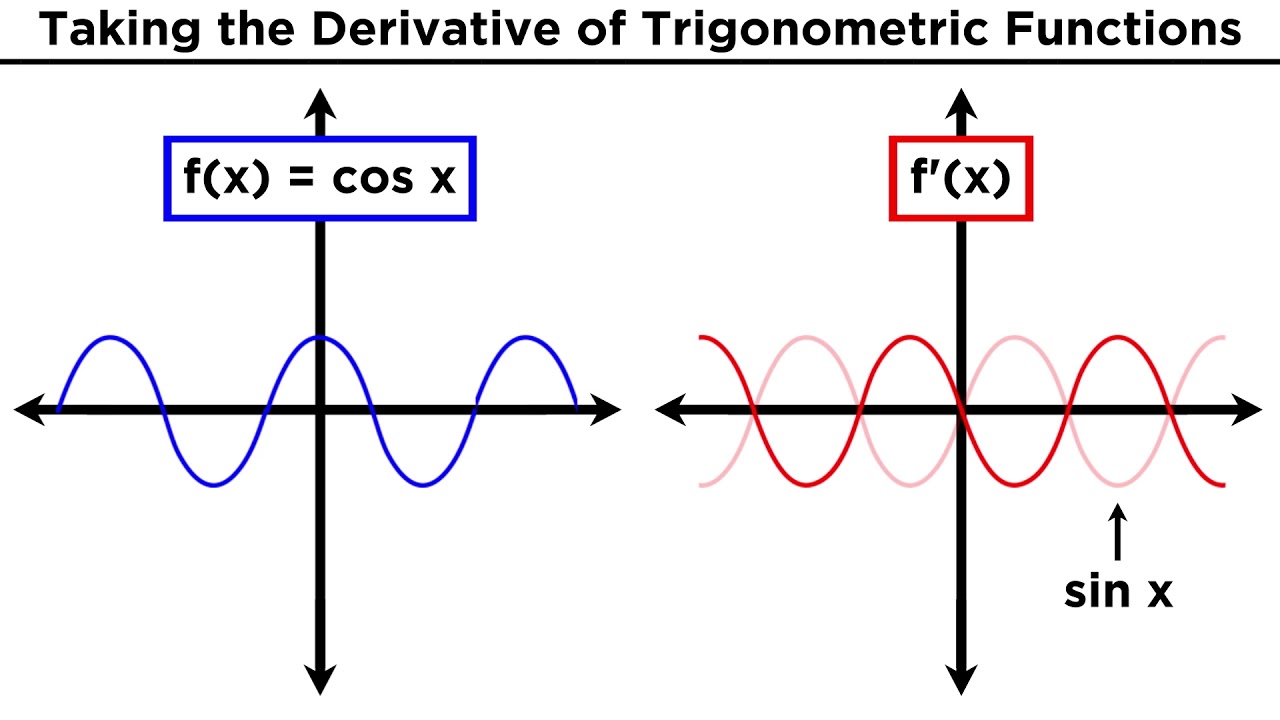
- ✏️ The derivative of sin(x) is cos(x), and the derivative of cos(x) is -sin(x).
- 📉 To prove the derivative of a function, the limit concept is essential, specifically using the limit as h approaches zero.
- 🔍 Understanding the sum and difference formulas for trigonometric functions is necessary for differentiating complex functions.
- 🔗 The limit of sin(x)/x as x approaches zero equals one, which is useful in derivative proofs.
- 🚀 Examples demonstrate how to apply derivative rules, such as finding the derivative of sin(3x) and cos(2x - 3).
- 🎓 Students are encouraged to prove derivatives independently and utilize established derivative formulas confidently.
Q & A
What is the definition of a derivative according to the script?
-A derivative, or turunan, is a measure of how a function changes as the input value changes. It indicates how a quantity varies in response to changes in another quantity.
What physical example is given to explain the concept of a derivative?
-The derivative of the position of a moving object with respect to time is given as instantaneous velocity.
What is the fundamental theorem of calculus mentioned in the script?
-The fundamental theorem of calculus states that the antiderivative is equivalent to integration, linking the concepts of derivatives and integrals.
How does the script describe the relationship between trigonometric functions and derivatives?
-The script emphasizes that understanding the derivatives of trigonometric functions is crucial, highlighting their significance in calculus.
What is the formula for the derivative of sin(x) as discussed in the video?
-The derivative of sin(x) is stated as cos(x).
What mathematical concept is used to prove the derivative of sin(x)?
-The concept of limits is used to prove that the derivative of sin(x) equals cos(x).
What trigonometric identity is mentioned to aid in proving derivatives?
-The sum and difference identities of trigonometric functions are mentioned as important for proving derivatives.
What are the steps involved in proving that the derivative of sin(x) is cos(x)?
-The proof involves using the limit definition of a derivative, substituting values, applying trigonometric identities, and simplifying the expression.
What is the derivative of cos(x) as explained in the script?
-The derivative of cos(x) is given as -sin(x).
What emphasis does the speaker place on students regarding the use of derivatives?
-The speaker encourages students to practice proving the derivatives themselves to gain confidence and understanding before applying them.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)