Lec 25 C - Slope of a Quadratic Function
Summary
TLDRThe transcript discusses how to calculate the slope of a quadratic curve, specifically focusing on the function y = x². It explains that while a line has a constant slope, a curve like y = x² has a variable slope, calculated as 2ax + b for quadratic functions. The concept of symmetry, tangents, and how changes in x and y affect slope calculations are explored. It also addresses why the minimum or maximum of a quadratic function occurs at x = -b/2a, where the slope becomes zero, highlighting how slope reflects the rate of change in the function.
Takeaways
- 📉 The slope of a curve, such as \( y = x^2 \), is not constant and must be evaluated based on changes in \( y \) with respect to changes in \( x \).
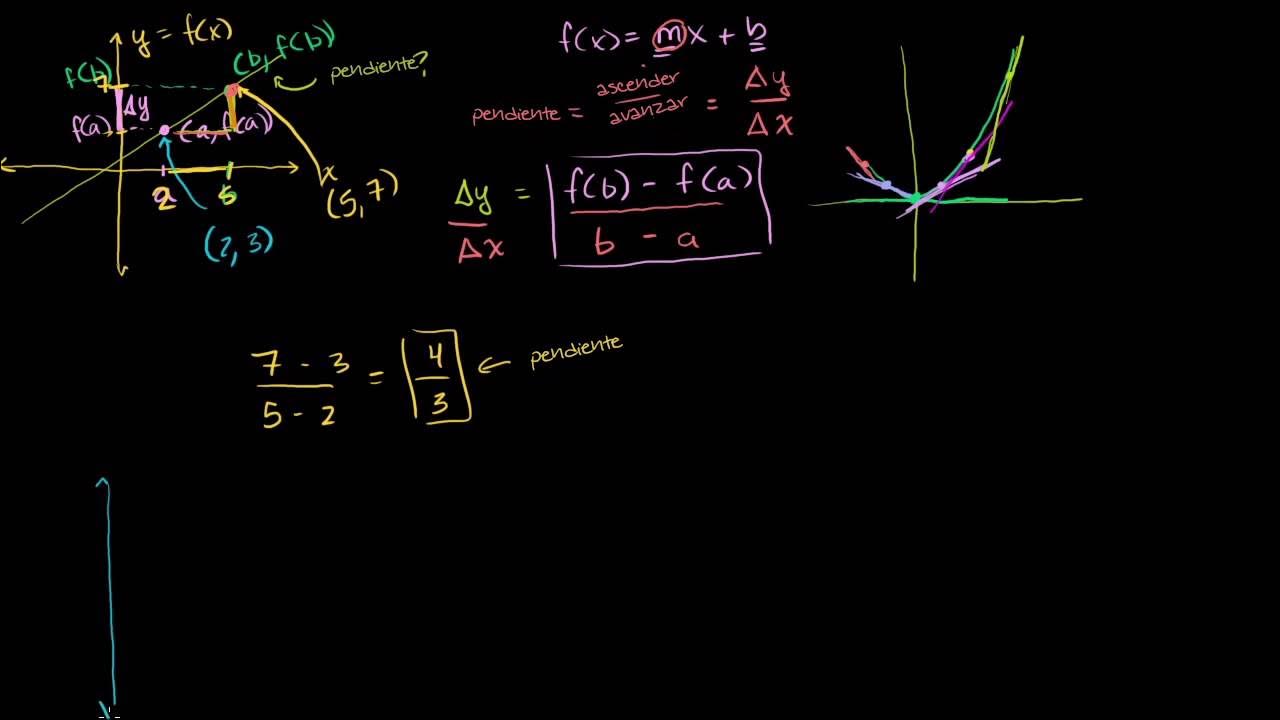
- 🧮 The slope is calculated as the difference in \( y \) values divided by the constant change in \( x \), but this applies to straight lines, not curves.
- 🔄 The function \( y = x^2 \) has symmetry about the y-axis, with its minimum value at 0.
- 📐 Slope in general can be related to the angle of inclination, and for curves, the tangent line at a point determines the slope at that point.
- 🔍 The slope of a quadratic function can be generalized as \( 2ax + b \), where the slope depends on \( a \) and \( b \), not on the constant \( c \).
- ✏️ The second differences in the y-values confirm the relationship with the slope, and the constant factor of 2 shows a consistent pattern in the slope calculation.
- ⚖️ The axis of symmetry of a quadratic function is at \( x = -\frac{b}{2a} \), where the slope is 0, indicating a minimum or maximum.
- 📊 The midpoint method is used to estimate the slope at various points along the curve, showing the varying slope values for quadratic functions.
- 🌀 The slope of a quadratic function is variable, unlike a straight line where the slope is constant. This slope defines the rate of change of the function.
- 📏 The slope reaching 0 at the vertex of a quadratic function explains why this point represents a maximum or minimum, depending on the direction of the curve.
Q & A
What is the significance of the axis of symmetry in the function being discussed?
-The axis of symmetry in the function is important because it reflects the point where the function is symmetric on both sides. For the quadratic function y = x², the axis of symmetry is the y-axis (x = 0), as the function is symmetric about this axis.
How is the slope of the curve initially calculated?
-The slope is calculated using the change in y over the change in x (Δy/Δx). Since the change in x is constant (equal to 1), the focus is on calculating the differences between consecutive y-values to estimate the slope at various points.
Why is the slope calculated between two points not the true slope of the curve?
-The slope calculated between two points assumes a straight line between them, which doesn't accurately represent the slope of a curve. For a curve, the true slope is the slope of the tangent line at a specific point, not the slope between two discrete points.
How is the slope at a specific point on a curve determined?
-The slope at a specific point on a curve is determined by finding the tangent to the curve at that point. The slope of the tangent line represents the rate of change of the curve at that point.
What is the relation between the angle of inclination (θ) and the slope of the curve?
-The slope of a line is related to the angle of inclination (θ) through the function tan(θ). The slope is defined as the tangent of the angle between the line and the positive x-axis.
What pattern is observed when looking at the second differences of the y-values?
-The second differences of the y-values turn out to be constant, indicating that the rate of change of the slope (i.e., the second derivative) is uniform, which is characteristic of a quadratic function.
What conclusion can be drawn about the slope of a quadratic function?
-The slope of a quadratic function is not constant. It varies according to the formula 2ax + b, where a and b are coefficients from the general quadratic equation ax² + bx + c.
How is the midpoint concept used to understand the slope of the curve?
-The midpoint of two x-values is used to approximate the slope at a point. By calculating the slope between two points and dividing by 2, the slope at the midpoint can be inferred, helping to approximate the slope of the curve at that specific location.
What is the significance of the point x = -b/2a in a quadratic function?
-The point x = -b/2a is where the slope of the quadratic function is 0, indicating that the function has reached either its minimum or maximum at this point. This is also why this point is called the vertex of the parabola.
Why does the slope of a quadratic function depend on 'a' and 'b' but not 'c'?
-The slope of a quadratic function depends on 'a' and 'b' because they influence the rate of change of the function. The constant term 'c' only affects the vertical shift of the graph but does not impact the rate at which y changes with respect to x.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

¿Cómo GRAFICAR una función CUADRÁTICA? RAÍCES, VÉRTICE, ORDENADA AL ORIGEN y MÁS

Quadratic Functions, How to Graph Quadratic Functions, Quadratic Function Graph

12.1 Gradients of curves (PURE 1- Chapter 12: Differentiation)

Cara Menentukan Fungsi Kuadrat Jika Diketahui Titik Potong Terhadap Sumbu-X

Calculating slope of tangent line using derivative definition | Differential Calculus | Khan Academy
Cálculo: Derivadas 1 (nueva versión HD)
5.0 / 5 (0 votes)
