Sumas de Riemann por la izquierda y por la derecha como sobreestimaciones y subestimaciones
Summary
TLDREl guion trata sobre la aproximación del área bajo una curva usando sumas de Riemann. Se explica cómo las sumas por la izquierda y por la derecha pueden sobreestimar o subestimar el área, respectivamente, dependiendo de si la función es estrictamente decreciente o creciente. Se ilustra con ejemplos específicos y se enfatiza la importancia de la elección de sub divisiones en la precisión de la aproximación.
Takeaways
- 📊 Se discute acerca de aproximar el área debajo de la gráfica de una función g(x) entre x=2 y x=8 utilizando sumas de Riemann.
- 🔍 Se menciona que las sumas de Riemann pueden ser estimaciones superiores o inferiores del área real.
- 📐 Se decide dividir el intervalo [2, 8] en tres subintervalos de igual tamaño para calcular las sumas de Riemann.
- 📈 Se utiliza la suma de Riemann por la izquierda, tomando el valor de la función en el lado izquierdo de cada subintervalo para calcular la altura de los rectángulos.
- 📉 Se indica que la suma de Riemann por la izquierda es una sobreestimación cuando la función disminuye estrictamente en el intervalo considerado.
- 🔺 Se explica que al usar el lado izquierdo de cada subintervalo para la suma de Riemann, se obtiene un valor de la función mayor que el promedio en ese intervalo, lo que lleva a una sobreestimación.
- ➡️ Se considera la suma de Riemann por la derecha, utilizando el valor de la función en el lado derecho de cada subintervalo para determinar la altura de los rectángulos.
- 📊 Se argumenta que la suma de Riemann por la derecha es una subestimación cuando la función es estrictamente decreciente en el intervalo.
- 📊 Se resalta que al usar el lado derecho de cada subintervalo, el valor de la función es menor que el promedio en ese intervalo, resultando en una subestimación del área.
- 🔄 Se señala que si la función fuese estrictamente creciente, los roles de las sumas de Riemann por la izquierda y por la derecha se intercambiarían.
- ⚖️ Se concluye que la elección de subestimación o sobreestimación depende de la función y de cómo se realicen las subdivisiones del intervalo.
Q & A
¿Qué es la suma de Riemann por la izquierda y cómo se calcula?
-La suma de Riemann por la izquierda es una aproximación del área debajo de una curva, donde se utilizan los valores de la función en el lado izquierdo de cada subdivisión para calcular la altura de los rectángulos que se suman.
¿Por qué la suma de Riemann por la izquierda es una sobreestimación para una función que disminuye estrictamente?
-Es una sobreestimación porque el lado izquierdo de cada subdivisión tiene un valor de la función más grande que en cualquier otro punto dentro de la subdivisión, lo que resulta en rectángulos más grandes que el área que se intenta aproximar.
¿Cómo se determina el número de subdivisiones para la aproximación?
-El número de subdivisiones se decide de manera arbitraria, pero más subdivisiones suelen dar una aproximación más precisa al área.
¿Qué es la suma de Riemann por la derecha y cómo se calcula?
-La suma de Riemann por la derecha es otra forma de aproximar el área debajo de una curva, donde se usan los valores de la función en el lado derecho de cada subdivisión para determinar la altura de los rectángulos.
¿Por qué la suma de Riemann por la derecha es una subestimación para una función que disminuye estrictamente?
-Es una subestimación porque el lado derecho de cada subdivisión tiene un valor de la función más pequeño que el promedio del valor de la función sobre el intervalo, lo que resulta en rectángulos más pequeños que el área que se intenta aproximar.
¿Cuál es la relación entre el tipo de función y si la suma de Riemann por la izquierda o derecha es una sobreestimación o subestimación?
-Si la función aumenta estrictamente, la suma de Riemann por la izquierda sería una subestimación y la por la derecha sería una sobreestimación. Esto se debe a que los valores de la función en el lado izquierdo serían menores y en el lado derecho serían mayores que el promedio del intervalo.
¿Cómo se pueden visualizar las subdivisiones para calcular las sumas de Riemann por la izquierda y por la derecha?
-Las subdivisiones se pueden visualizar dividiendo el intervalo de interés en partes iguales y luego trazando rectángulos usando los valores de la función en el lado izquierdo para la suma por la izquierda y en el lado derecho para la suma por la derecha.
¿Qué pasa si la función no aumenta ni disminuye estrictamente? ¿Cómo se afecta la aproximación?
-Si la función no es estrictamente creciente ni decreciente, la elección de los lados izquierdo o derecho para la aproximación puede afectar la precisión de la suma de Riemann, pudiendo resultar en sobreestimaciones o subestimaciones dependiendo de la forma específica de la función.
¿Cómo se pueden mejorar las aproximaciones usando las sumas de Riemann?
-Se pueden mejorar las aproximaciones aumentando el número de subdivisiones y/o refinando la elección de los puntos de evaluación dentro de cada subdivisión para que mejor representen el comportamiento de la función.
¿Cuál es la importancia de entender las sumas de Riemann para la aproximación de áreas bajo curvas?
-Las sumas de Riemann son fundamentales para entender la integración definida, que es una herramienta matemática para calcular áreas y otras propiedades integrales de funciones continuas y discontinuas.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Ordenar las sumas de Riemann por la izquierda y por la derecha
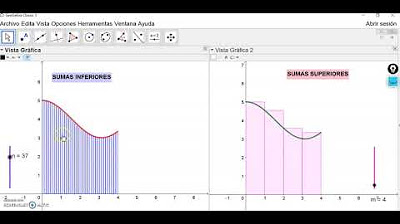
SUMAS DE RIEMANN
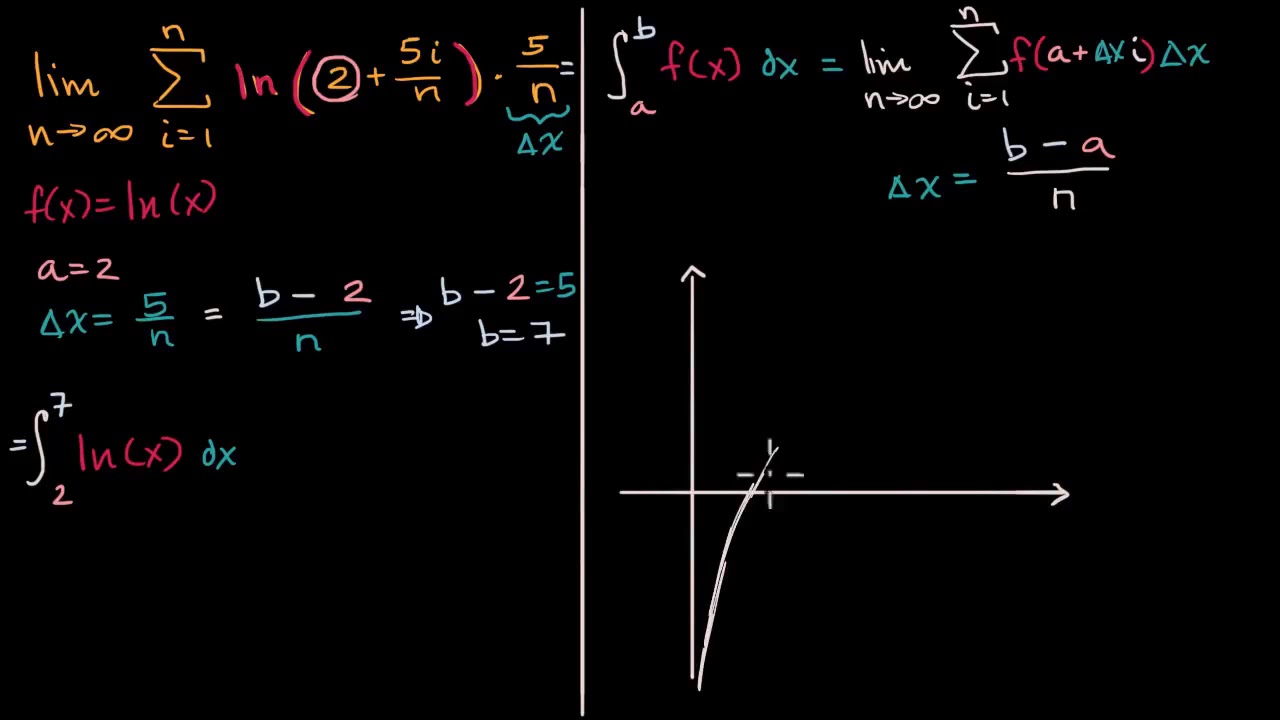
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español

Área aproximada por rectángulos (inscritos y circunscritos)

Cuadratura de Gauss parte 1
5.0 / 5 (0 votes)
