Ordenar las sumas de Riemann por la izquierda y por la derecha
Summary
TLDREl guion trata sobre el cálculo del área bajo una curva continua utilizando sumas de Riemann. Se discute cómo las sumas de Riemann por la izquierda y por la derecha pueden sobreestimar o subestimar el área real, respectivamente, dependiendo de la forma de la función g(x). Se invita a los espectadores a realizar la aproximación dividiendo el intervalo y eligiendo subintervalos no necesariamente iguales, analizando el impacto de estas elecciones en la precisión de la aproximación.
Takeaways
- 📊 La función continua g está gráfica y se desea calcular el área bajo la curva entre x = -7 y x = 7.
- 🎨 Se está considerando el uso de las sumas de Riemann para aproximar el área de interés, que está marcado en azul.
- 📉 Se pide ordenar las áreas de menor a mayor al final del ejercicio.
- 📐 Se describe cómo realizar sumas de Riemann por la izquierda y por la derecha para aproximar áreas.
- 📌 Se menciona que las subdivisiones no tienen que ser iguales y se puede hacer una subdivisión desigual.
- 🔼 Al usar la suma de Riemann por la izquierda, se tiende a sobreestimar el área debido a que el valor de la función en el lado izquierdo es mayor que en cualquier otro punto del intervalo.
- 🔽 Al usar la suma de Riemann por la derecha, se tiende a subestimar el área porque el valor de la función en el lado derecho es menor que en cualquier otro punto del intervalo.
- ➡️ Se hace una comparación entre la suma de Riemann por la izquierda, por la derecha y el área real para mostrar cómo se ven.
- 📊 Se sugiere que para una función que disminuye o se mantiene constante, la suma de Riemann por la izquierda sobreestimará y la por la derecha subestimará.
- 📝 Se concluye que si se ordenan las áreas, la suma de Riemann por la derecha es la menor (subestimada), seguida del área real y luego la suma de Riemann por la izquierda que es la mayor (sobreestimada).
Q & A
¿Qué función se está analizando en el guion?
-El guion no especifica la ecuación de la función, pero se menciona que se está interesado en el área bajo la curva de la función continua 'g' entre x = -7 y x = 7.
¿Cuál es el propósito de las sumas de Riemann?
-Las sumas de Riemann se utilizan para aproximar el área bajo la curva de una función continua.
¿Qué color representa el área de interés en el guion?
-El área de interés se representa en color azul.
¿Cómo se sugiere ordenar las áreas de menor a mayor en el guion?
-Se sugiere ordenar las áreas de menor al inicio a mayor al final.
¿Qué método se utiliza para aproximar el área en el guion?
-Se utiliza el método de las sumas de Riemann, donde se pueden hacer subdivisiones arbitrarias y no necesariamente iguales.
¿Qué tipo de aproximación representa la suma de Riemann por la izquierda?
-La suma de Riemann por la izquierda representa una sobreestimación del área real.
¿Por qué la suma de Riemann por la izquierda está sobreestimada para la función mencionada?
-Está sobreestimada porque la función disminuye o se mantiene constante, y el valor de la función en el lado izquierdo de cada subdivisión es mayor que cualquier otro valor de la función sobre ese intervalo.
¿Qué sugiere hacer el guion para las subdivisiones?
-El guion sugiere hacer pocas subdivisiones y no necesariamente iguales para mostrar que las sumas de Riemann son válidas.
¿Cuál es la diferencia entre la suma de Riemann por la izquierda y por la derecha?
-La suma de Riemann por la izquierda utiliza el valor de la función en el lado izquierdo de la subdivisión, mientras que por la derecha se usa el valor del lado derecho.
¿Por qué la suma de Riemann por la derecha está subestimada para la función mencionada?
-Está subestimada porque la función disminuye o se mantiene constante, y el valor de la función en el lado derecho de la subdivisión es menor que cualquier otro valor de la función sobre ese intervalo.
¿Cómo se ordenan las sumas de Riemann y el área real de menor a mayor?
-Se ordenan de la siguiente manera: la suma de Riemann por la derecha (subestimada), el área real bajo la curva y la suma de Riemann por la izquierda (sobreestimada).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
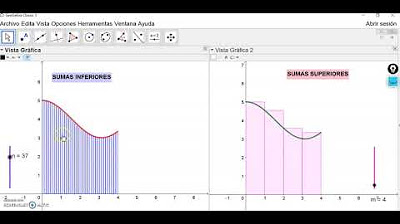
SUMAS DE RIEMANN

Sumas de Riemann por la izquierda y por la derecha como sobreestimaciones y subestimaciones

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español
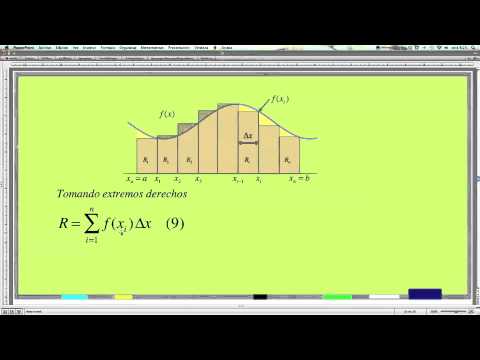
Calculo Integral 04: La integral definida. The definite integral.
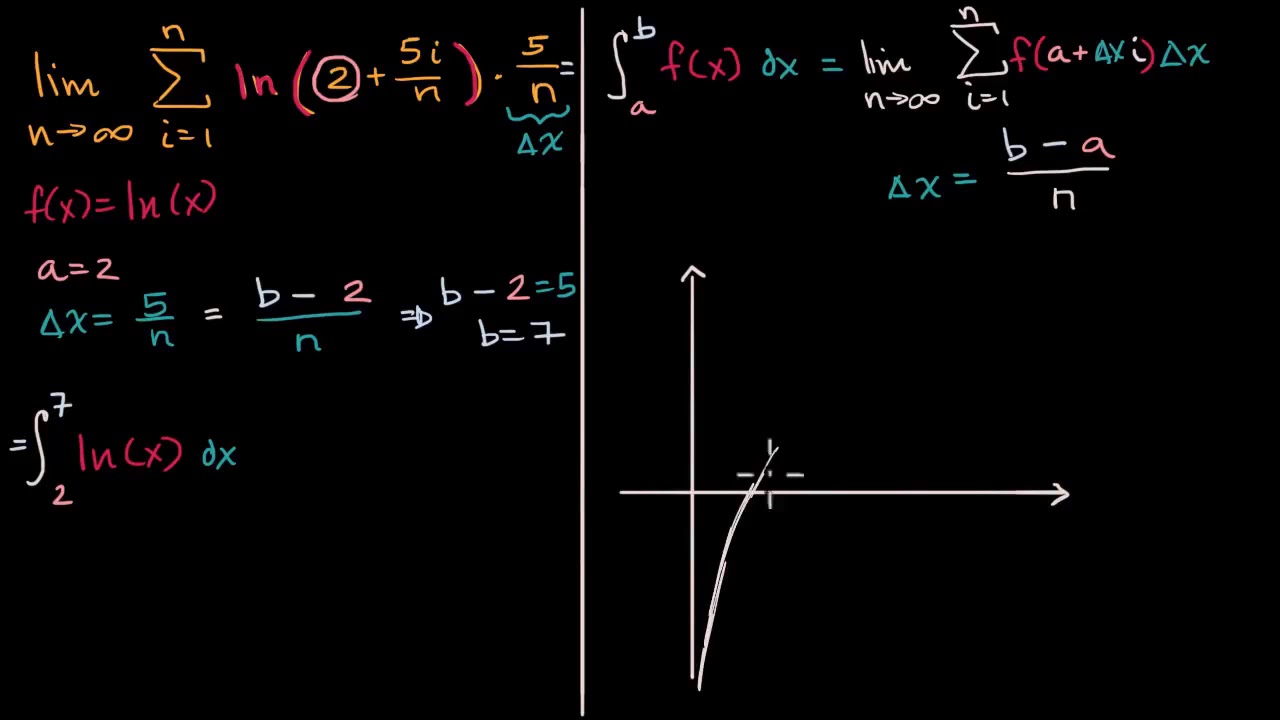
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Cálculo Integral 01:Área bajo una curva. Area under a curve
5.0 / 5 (0 votes)
