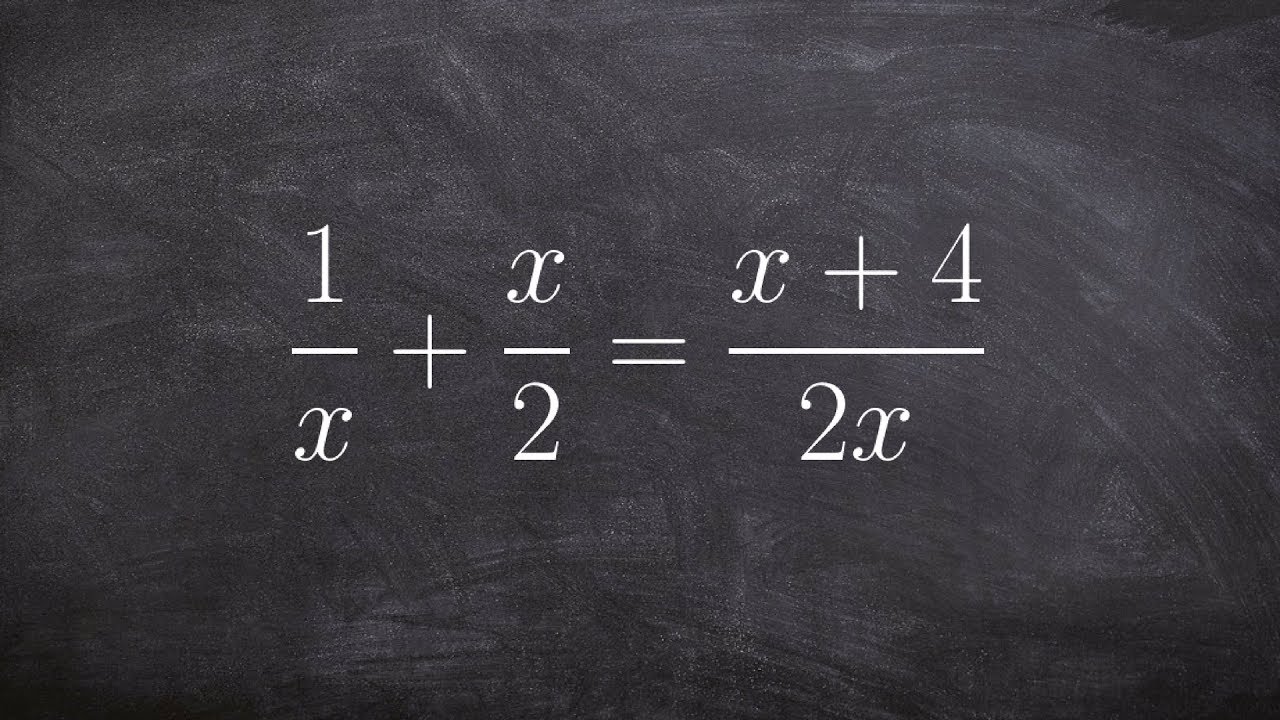Solving Rational Equations

Summary

This lesson focuses on solving rational equations by eliminating fractions and finding the least common multiple. The instructor demonstrates step-by-step solutions for various examples, including simplifying equations, factoring, and applying cross-multiplication. Techniques for finding x values are explored, with a final example involving factoring a quadratic expression and solving for x, yielding multiple solutions.

Takeaways

• 🔍 The lesson focuses on solving rational equations by eliminating fractions to simplify the problem.
• 📚 The first example demonstrates finding the least common multiple (LCM) of 8, 5, and 10, which is 40, to clear fractions from the equation.
• 🧩 After clearing fractions, the solution involves basic arithmetic operations to solve for x, resulting in x = 1/4 for the initial example.
• 📉 In the second problem, multiplying both sides by x eliminates the denominators, leading to a quadratic equation which factors to find x = 4 and x = 2.
• ✅ The third example uses cross-multiplication to transform the equation into a linear one, solving for x = 5.
• 🤔 The fourth problem involves taking the square root of both sides after cross-multiplication, yielding two potential solutions, x = 6 and x = -6.
• 🔢 For the fifth example, cross-multiplication and simplification lead to a solution of x = 7 after combining like terms.
• 📈 The sixth example uses the LCM of 2 and 3, which is 6, to eliminate fractions and solve for x = 1.
• 📉 The seventh problem involves finding a common denominator and simplifying to form a quadratic equation, which factors to x = 2 and x = -1.
• 🔗 The last example involves factoring a difference of squares and clearing fractions to form a quadratic equation, solving for x = 13 and x = -3.

Q & A

What is the first step to solve a rational equation involving fractions?

The first step is to find the least common multiple (LCM) of the denominators and then multiply every fraction by that LCM to eliminate the fractions.

How do you find the least common multiple (LCM) of 8, 5, and 10 from the transcript?

You list the multiples of each number and identify the smallest number that appears in all lists. In this case, the multiples of 5 are 5, 10, 15, etc., multiples of 8 are 8, 16, 24, 32, 40, and multiples of 10 include 10, 20, 30, 40. The LCM is 40.

What is the value of x in the equation 5/8 - 3/5 = x/10?

After clearing the fractions by multiplying by the LCM (40), you get 25 - 24 = 4x/10, which simplifies to 1 = 4x/10. Solving for x gives x = 1/4.

How do you handle the equation x + 8/x = 6?

You multiply both sides by x to eliminate the fraction, which gives x^2 + 8 = 6x. Then, you rearrange the equation to x^2 - 6x + 8 = 0 and factor it to (x - 4)(x - 2) = 0, giving x = 4 and x = 2.

What is the process for solving the equation (x + 3)/(x - 3) = 12/3?

You cross-multiply to get 12(x - 3) = 3(x + 3). Simplifying gives 12x - 36 = 3x + 9. Then, you combine like terms and solve for x, which results in x = 5.

How do you solve the equation 9/x = x/4?

You cross-multiply to get 9 * 4 = x^2, which simplifies to 36 = x^2. Taking the square root of both sides gives x = ±6.

In the equation 4/(x - 3) = 9/(x + 2), what is the step after cross-multiplying?

After cross-multiplying, you get 4(x + 2) = 9(x - 3). Expanding and simplifying leads to 4x + 8 = 9x - 27, and then you solve for x, which results in x = 7.

What is the least common multiple (LCM) of 2 and 3, and how is it used in the equation (x + 2)/3 = (x + 9)/2?

The LCM of 2 and 3 is 6. Multiplying both sides of the equation by 6 eliminates the fractions, leading to 2x + 4 = 3x + 27/2, which simplifies to x = 1.

How do you solve the equation 4/x + 8/(x + 2) = 4?

You multiply both sides by the common denominator x(x + 2), which gives 4(x + 2) + 8x = 4x^2 + 8x. Simplifying and solving the quadratic equation gives x = 2 and x = -1.

In the final example of the transcript, how do you simplify the equation (x + 5)/(x - 5) - 5/(x + 5) = 14/(x^2 - 25)?

You factor x^2 - 25 as (x + 5)(x - 5) and multiply both sides by this expression to clear the fractions. Simplifying leads to x^2 - 10x - 39 = 0, which factors to (x - 13)(x + 3) = 0, giving x = 13 and x = -3.

Outlines

00:00

📚 Solving Rational Equations

This paragraph introduces the process of solving rational equations with examples. The first example involves simplifying a complex fraction and finding the least common multiple (LCM) of 8, 5, and 10, which is 40. The fractions are then multiplied by 40 to eliminate them, leading to the solution x = 1/4. The second example shows how to solve an equation with a variable in the denominator by multiplying both sides by x to eliminate the fraction and then factoring to find x = 4 and x = 2. The third example uses cross-multiplication to solve an equation, resulting in x = 5. The fourth example involves taking the square root of both sides to find two possible solutions, x = ±6. The final example in this paragraph demonstrates cross-multiplication and solving for x = 7 after simplifying the equation.

05:02

🔍 Advanced Rational Equation Techniques

This paragraph delves into more complex rational equation problems. The first example involves finding the LCM of 2 and 3, which is 6, and multiplying through to eliminate fractions, leading to the solution x = 1. The second example requires finding a common denominator of x(x + 2) and simplifying to find two solutions, x = 2 and x = -1. The third example involves factoring a difference of squares and multiplying through to eliminate fractions, resulting in two potential solutions, x = 13 and x = -3. The paragraph demonstrates a step-by-step approach to solving rational equations, emphasizing the importance of finding common denominators, factoring, and simplifying equations to isolate the variable.

10:07

📘 Final Rational Equation Challenges

The final paragraph presents a challenging rational equation that requires factoring and careful manipulation to solve. The equation involves a difference of squares, which is factored into (x + 5)(x - 5). The fractions are eliminated by multiplying through by the common denominator, and the equation is simplified to x^2 - 5x - 39 = 0. Factoring this quadratic equation yields (x - 13)(x + 3) = 0, leading to the solutions x = 13 and x = -3. This example showcases the application of algebraic techniques to solve more intricate rational equations.

Keywords

💡Rational Equations

Rational equations are equations that contain one or more rational expressions, which are fractions where the numerator and denominator are polynomials. In the video, the main theme revolves around solving such equations by finding the value of the variable that makes the equation true. Examples include '5 over 8 minus 3 over 5' and 'x plus 3, divided by x minus 3'.

💡Least Common Multiple (LCM)

The least common multiple of two or more integers is the smallest number that is a multiple of each of the integers. In the script, the LCM is used to clear away fractions by finding a common denominator, such as finding the LCM of 8, 5, and 10 to be 40, which helps in simplifying the rational equation.

💡Cross Multiply

Cross multiplying is a technique used to solve equations involving two fractions by multiplying the numerator of one fraction by the denominator of the other and vice versa. This method is used in the script to transform equations like 'x plus 3, divided by x minus 3 equals 12 over 3' into a form that can be easily solved.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of its factors. In the context of the video, factoring is used to simplify and solve equations, such as 'x squared minus 5x minus 39' by finding two numbers that multiply to -39 and add up to -10, leading to the factors 'x minus 13' and 'x plus 3'.

💡Distributing

Distributing, also known as the distributive property, involves multiplying a term by each term inside a parenthesis. In the script, distributing is used to simplify expressions like 'x times x minus 5', which becomes 'x squared minus 5x'.

💡Combining Like Terms

Combining like terms is the process of adding or subtracting coefficients of terms that have the same variable raised to the same power. In the script, this is used to simplify expressions, such as '8x minus 12x' which simplifies to '-4x'.

💡Solving for x

Solving for x refers to finding the value of the variable x that satisfies the equation. The script provides multiple examples of this process, such as solving '25 minus 24 equals 1' to find that 'x equals one fourth'.

💡Variable Cancellation

Variable cancellation occurs when a variable in the numerator and denominator of a fraction cancels each other out, simplifying the expression. In the script, this is seen when '8 over x times x' simplifies to just '8' because the x's cancel.

💡Equation Transformation

Equation transformation involves manipulating an equation into a different form to make it easier to solve. The script demonstrates this by transforming equations like 'x plus eight over x equals 6' into a form where x can be isolated and solved.

💡Roots of an Equation

The roots of an equation are the values of the variable that make the equation true. In the context of the video, after cross-multiplying 'nine divided by x equals x over four', taking the square root of both sides yields two roots, 'plus or minus 6'.

💡Simplifying Fractions

Simplifying fractions involves reducing a fraction to its simplest form by dividing the numerator and denominator by their greatest common divisor. Although not explicitly mentioned, the process of simplifying is implied in the script when finding the LCM to clear fractions.

Highlights

Introduction to solving rational equations.

Method to clear fractions by finding the least common multiple (LCM).

Example of solving 5/8 - 3/5 = x/10 by using LCM of 40.

Technique of multiplying each fraction by the LCM to eliminate denominators.

Solving the equation by simplifying and finding x = 1/4.

Approach to solving the equation x + 8/x = 6 by multiplying both sides by x.

Factoring and solving for x in the equation x^2 - 6x + 8 = 0.

Finding the solutions x = 4 and x = 2 for the equation.

Cross-multiplication method for equations involving two fractions.

Solving x + 3/(x - 3) = 12/3 by cross-multiplication and simplification.

Determining x = 5 for the given equation.

Cross-multiplication for equations with fractions separated by an equal sign.

Solving 9/x = x/4 by taking the square root of both sides.

Finding two solutions, x = 6 and x = -6, for the equation.

Solving complex rational equations by cross-multiplication and factoring.

Example of solving 4/(x - 3) = 9/(x + 2) by cross-multiplication and simplification.

Determining x = 7 for the equation after simplification.

Using LCM to eliminate fractions in complex rational equations.

Solving x + 2/3 + 4/(x + 2) = x + 9/2 by multiplying by the LCM.

Finding x = 1 by simplifying and solving the resulting equation.

Solving rational equations with a common denominator by factoring and simplification.

Example of solving 4/x + 8/(x + 2) = 4 by finding a common denominator and simplifying.

Determining the solutions x = 2 and x = -1 for the equation.

Advanced technique of factoring and solving rational equations with quadratic denominators.

Solving i(x)/(x + 5) - 5/(x - 5) = 14/(x^2 - 25) by factoring and clearing fractions.

Finding the solutions x = 13 and x = -3 for the equation.

Transcripts

now in this lesson we're going to focus

on solving

rational equations

so let's start with our first example

5 over 8

minus 3 over 5

and let's set that equal to

x over 10.

what do we need to do

in order to find the value of x

what would you do

the best thing we can do is clear away

all fractions

we have an eight a five and a ten

what is the least common multiple of

eight five and ten

well we can make a list

multiples of five are five ten fifteen

and so forth

multiples of 8

are 8 16 24

32 and 40.

multiples of 10

also include 40. so 40 is the least

common multiple

let's multiply every fraction

by 40.

so what's 5

over 8 times 40

you can do 5 times 40 which is 200 and

then divide 200 by 8 or

you can do 40 divided by 8 which is 5

times the 5 on top

and that's going to be 25

now what about three fifths of 40

40 divided by five is eight eight times

three is twenty four

and the last one

forty divided by ten is four times x

that's four x

twenty five minus twenty four is one

and so x

is equal to one fourth so that's the

answer

here's the next problem x plus eight

over x is equal to 6.

feel free to pause the video and work on

this example

so what we're going to do in this

problem we're going to multiply both

sides by x

so x times x is x squared

and then 8 over x times x the x

variables will cancel it's just going to

be 8 and 6 times x is 6x

now let's move the 6x from the right

side

to the left side on the right side is

positive 6x but on the left side it's

going to be negative

now we can factor it

what two numbers multiply to eight but

add up to negative six

this is negative four and two

so it's x minus four times x minus two

and so we can clearly see that x is

equal to positive four

and positive two

and so that's it

here's the next one

x plus 3

divided by

x minus 3 let's say that's equal to 12

over 3.

whenever you have two fractions

separated by an equal sign what you want

to do is you want to cross multiply

so 12

times x minus 3 is 12x

minus 36

and 3 times x plus 3

that's 3x

plus 9.

now let's subtract both sides by 3x

and let's add 36 to both

sides 12x minus 3x is 9x

9 plus 36 is 45

and 45

divided by 9 is 5.

so x

is equal to 5.

try this one

nine divided by x is x over four

so once again we have two fractions

separated by an equal sign

let's cross multiply

x times x is x squared

and 9 times 4 is 36

so all we need to do is take the square

root of both sides

the square root of 36

is plus or minus 6. so there's two

answers positive six and negative six

now what about this one four

divided by x minus three

and let's say that's equal to nine

over x plus two

so for this problem as well cross

multiply

so four times x plus two that's

four x plus eight

and then nine times x minus three that's

nine x minus twenty seven

so let's subtract both sides by 4x

and let's add 28 i mean not 28 but

rather 27 to both sides

8 plus 27 that's 35

9 minus 4 is 5.

so all we need to do now is divide by 5.

35 divided by 5 is 7.

so x

is equal to 7.

now let's say that we have x

plus two

divided by three

plus

four

and let's say that's equal to x plus

nine

divided by two

find the value of x

the least common multiple of two and

three is six

so let's multiply everything by six to

get rid of the fractions

six divided by three is two now let's

multiply two by x plus two

and that's going to be two x plus four

now four times six

is twenty four

and six divided by two is three and

three times

x plus nine that's going to be 3x

plus 27

so now let's combine 4 and 24 which is

28

now let's subtract both sides by 2x

and also by 27

28 minus 27 is one

3x minus 2x is x

so therefore x is equal to one

here's the next problem

four divided by x

plus

eight divided by x plus two

let's set that equal to four find the

value of x

so in this case the common denominator

is x

times x plus two

if we multiply 4 over x by

x x plus 2

the x variables will cancel

and so that's going to leave behind 4

times x plus 2

which if we distribute 4 is going to be

4x

plus 8.

now x plus 2 will cancel leaving behind

x times 8 or simply 8x

and then here we'll have 4 times x times

x plus 2

which is 4x

x plus 2.

now we can add 4x and 8x

that's going to be 12x

and now let's distribute the 4x 4x times

x is 4x squared 4x times 2 is 8x

everything on the left side let's move

it to the right side

so instead of having positive 12x on the

left side it's going to be negative 12x

on the right side

and 8 is going to change to negative 8.

now let's combine like terms

8x minus 12x is negative 4x

so now what we need to do is factor

we can take out a four

and this will leave us with x squared

minus x instead of plus x

minus two now two numbers that multiply

to negative two but at negative one

is going to be a negative two and

positive one

so it's gonna be x minus two times x

plus one

so if we set each factor equal to zero

we can see that x

is equal to two and x is equal to

negative one

and so that's going to be the answer

to the problem

now let's try the last example

5

or rather

i'll take that back not 5 x

over x plus 5

minus

5

over x minus 5.

let's say that's equal to 14

over x squared minus 25.

go ahead and find the value of x now

what we should do first is factor x

squared minus 25

and that's going to be x plus five

times x minus five

now we need to clear away all fractions

so let's multiply the top well let's

multiply both sides the left side and

the right side

by x plus five

times x minus five the common

denominator

so if we take this fraction and multiply

it by these two we can see that x plus

five will cancel

leaving behind x

times x minus five

now if we take the second fraction

multiply by those two

the x minus five term will cancel

leaving behind five times x plus five

and then x plus 5 will cancel and x

minus 5 will cancel

leaving 14.

so now let's distribute x times x minus

5.

that's x squared minus 5x

and if we distribute the negative 5

it's going to be negative 5x

minus 25.

now let's subtract both sides by 14 and

let's combine like terms

negative 5x and negative 5x that's

negative 10x

negative 25 minus 14

that's negative 39.

what two numbers

multiplied to negative 39

but add to negative 10.

i'm thinking of negative 13 and 3

so this is going to be x

minus 13

x plus 3.

so therefore x is equal to 13

and negative 3.