Solving a rational Equation
Summary
TLDRThis video covers the process of solving a rational equation by eliminating fractions through multiplying by the least common denominator (LCD). The instructor explains how to identify the LCD and eliminate fractions, leading to a simplified quadratic equation. The equation is then factored and solved using the zero product property, resulting in two possible solutions. The walkthrough offers clear steps and guidance for solving rational equations, particularly for equations that involve quadratics.
Takeaways
- 🔢 Identifying the LCD (Least Common Denominator) is the first step to simplify the rational equation.
- ✖️ The LCD in this case is determined to be 2x, which divides into each of the denominators.
- 🧮 Multiply every term in the equation by the LCD to eliminate fractions.
- ➗ The denominators divide out after multiplying by the LCD, simplifying the equation to 2 + x^2 = x + 4.
- 📐 The equation becomes quadratic after simplifying, requiring factoring techniques.
- 📉 To factor, get all terms to one side and set the equation equal to zero.
- ✏️ Rearranging gives the equation x^2 - x - 2 = 0, which needs to be factored.
- 🔗 The equation factors into (x - 2)(x + 1) = 0.
- 🟰 Using the zero product property, solve the two linear equations: x - 2 = 0 and x + 1 = 0.
- ✅ The final solutions to the rational equation are x = 2 and x = -1.
Q & A
What is the first step in solving the rational equation in the script?
-The first step is to determine the Least Common Denominator (LCD) of all the fractions and multiply the entire equation by that LCD to eliminate the fractions.
How is the LCD determined in this specific equation?
-The LCD is determined by looking at the denominators: x, 2, and 2x. The smallest term that all of them divide into is 2x.
What happens when the equation is multiplied by the LCD?
-Multiplying by the LCD eliminates the denominators, leaving an equation without fractions.
What does the equation become after multiplying by the LCD?
-After multiplying by the LCD (2x), the equation becomes 2 + x² = x + 4.
What type of equation does the script mention it becomes after eliminating the fractions?
-The equation becomes a quadratic equation after eliminating the fractions.
What is the next step after identifying the equation as a quadratic?
-The next step is to move all the terms to one side of the equation, setting it equal to zero, to prepare for factoring.
How is the quadratic equation factored in this case?
-The quadratic equation x² - x - 2 = 0 is factored into (x - 2)(x + 1) = 0.
What is the zero product property, and how is it applied here?
-The zero product property states that if a product of two factors equals zero, then at least one of the factors must be zero. It's applied by setting each factor (x - 2) and (x + 1) equal to zero.
What are the solutions to the quadratic equation after applying the zero product property?
-The solutions are x = 2 and x = -1.
Why does the speaker subtract x and 4 during the process?
-The speaker subtracts x and 4 to move all terms to one side of the equation, making it easier to rewrite the quadratic equation in standard form for factoring.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
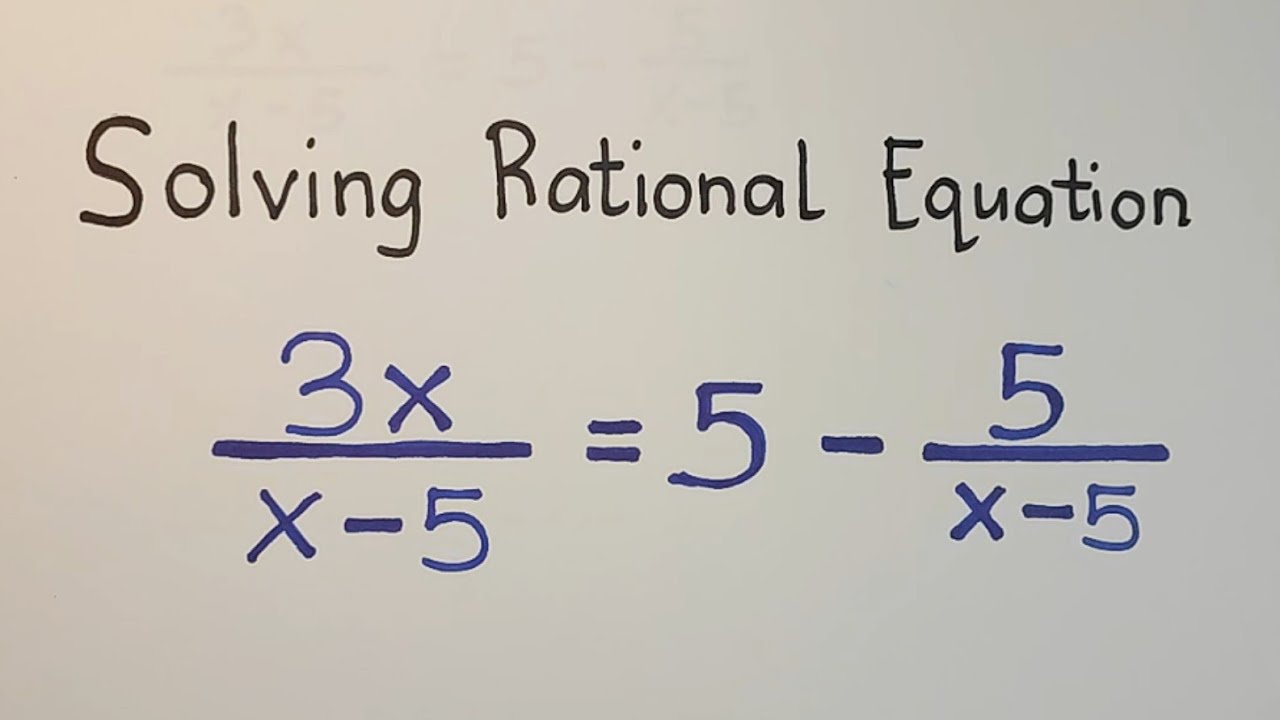
Solving Rational Equation with Whole Number - Part 2 - General Mathematics

Solving Rational Equations | General Mathematics

Addition and Subtraction of Rational Numbers - Operation on Rational Numbers

Solving Rational Equations (Easy Method)

MATEMATIKA 6 SD VIDEO 008 PENJUMLAHAN DAN PENGURANGAN PECAHAN

Le quattro operazioni fondamentali con le frazioni
5.0 / 5 (0 votes)