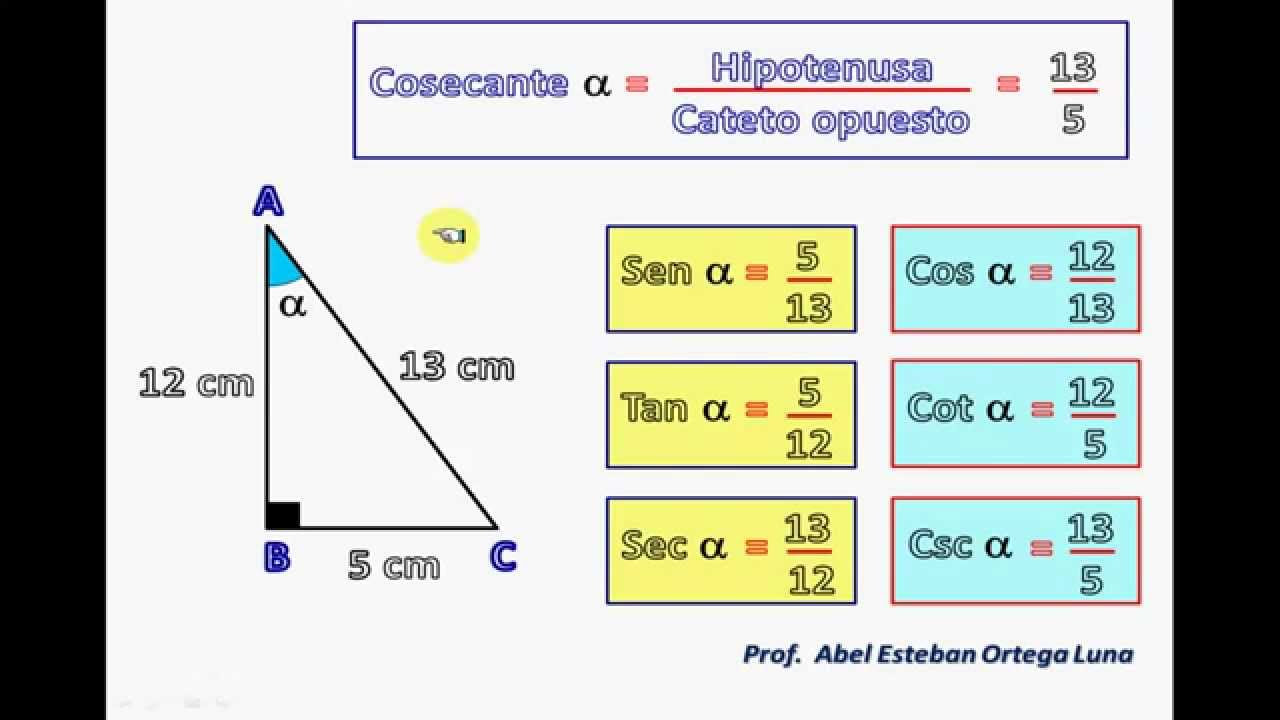
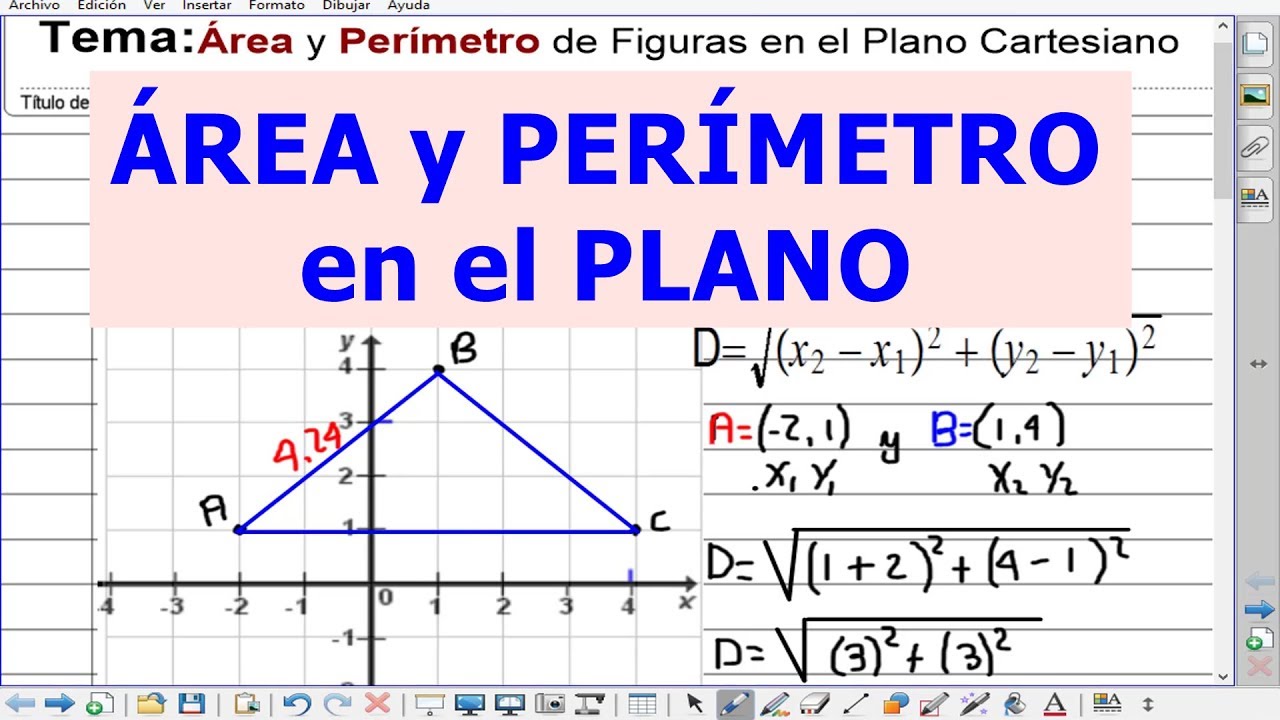
📚 ICFES 2024 - TRIGONOMETRÍA
Summary
TLDREl guion ofrece una explicación detallada de conceptos geométricos básicos como el área y el perímetro, utilizando ejemplos prácticos como figuras cuadradas y un triángulo rectángulo. Se describe cómo medir el perímetro como la longitud de un hilo alrededor de una figura y cómo calcular el área como la superficie. A través de la aplicación del teorema de Pitágoras, se resuelve un problema de encontrar la hipotenusa. El guion enfatiza la importancia de las unidades de medida en estas cálculos, como metros para el perímetro y metros cuadrados para el área, y destaca la distinción entre calcular el área y el perímetro, a pesar de que en algunos casos pueden dar resultados similares.
Takeaways
- 📏 La definición de perímetro es la medida de los bordes de una figura, como si se colocara un hilo alrededor de ella.
- 📐 El área se refiere a la superficie de un espacio, y se mide en metros cuadrados.
- 🔍 En el sistema MKS, el perímetro se mide en metros y el área en metros cuadrados.
- 📐 El cálculo del área de un cuadrado es el producto de sus lados (lado × lado).
- 📏 El perímetro de un cuadrado es la suma de sus cuatro lados (lado + lado + lado + lado).
- 🔢 El ejemplo del cuadrado con un lado de 2 cm muestra cómo calcular su área y perímetro.
- 📐 El cálculo del área de un cuadrado en el contexto de la imagen dada es la raíz cuadrada del producto de sus lados (√lado²).
- 🔢 En el ejemplo dado, el lado de un cuadrado con área de 64 m² es de 8 m, y con área de 36 m² es de 6 m.
- 📐 El teorema de Pitágoras se usa para calcular la hipotenusa de un triángulo rectángulo (hipotenusa² = cateto1² + cateto2²).
- 📏 En el triángulo rectángulo del ejemplo, la hipotenusa se calcula como √(8² + 6²) = √100 = 10 m.
- 📐 El perímetro del triángulo rectángulo se calcula sumando sus tres lados (6 m + 8 m + 10 m), dando un total de 24 m.
Q & A
¿Qué es el perímetro y cómo se mide?
-El perímetro es la medida de los bordes o límites de una figura. Se mide colocando un hilo alrededor de la figura y midiendo su longitud, y en el sistema MKS se expresa en metros.
¿Cómo se define el área y en qué unidad se mide?
-El área es la medida de la superficie de un espacio o figura. Se expresa en unidades de metros cuadrados cuando se mide en el sistema MKS.
Si se tiene un cuadrado con un lado de 2 cm, ¿cuál es su área y su perímetro?
-El área de un cuadrado se calcula como lado por lado, es decir, 2 cm * 2 cm = 4 cm². El perímetro se calcula sumando los cuatro lados, que sería 2 cm + 2 cm + 2 cm + 2 cm = 8 cm.
¿Cómo se relaciona el perímetro y el área en el ejemplo del cuadrado?
-En el ejemplo del cuadrado, el perímetro y el área no son iguales, pero ambos son medidas fundamentales de la figura. El perímetro mide la longitud de los bordes, mientras que el área mide la superficie.
Si el área de un cuadrado es 64 m², ¿cuál es su lado?
-Si el área de un cuadrado es 64 m², su lado se encuentra tomando la raíz cuadrada de 64, que es 8 m.
¿Cómo se calcula el área de un triángulo rectángulo?
-El área de un triángulo rectángulo se calcula como la base por la altura dividido entre 2. En el caso de los catetos, sería cateto 1 por cateto 2 dividido entre 2.
¿Qué es el teorema de Pitágoras y cómo se aplica en el ejemplo del triángulo rectángulo?
-El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. En el ejemplo, si los catetos miden 8 m y 6 m, la hipotenusa sería la raíz cuadrada de (8² + 6²) = 10 m.
Si un triángulo rectángulo tiene lados de 8 m y 6 m, ¿cuál es su perímetro?
-El perímetro de un triángulo rectángulo se calcula sumando los tres lados. Con la hipotenusa de 10 m, el perímetro sería 6 m + 8 m + 10 m = 24 m.
¿Por qué el cálculo del perímetro y el área puede dar el mismo resultado en el ejemplo del triángulo rectángulo?
-Es una coincidencia matemática en este caso específico, ya que el cálculo del perímetro (6 m + 8 m + 10 m) y el cálculo del área (6 m * 8 m / 2) ambos dan como resultado 24.
¿Cuál es la importancia de recordar que el teorema de Pitágoras solo se aplica a triángulos rectángulos?
-El teorema de Pitágoras es fundamental para calcular la hipotenusa en triángulos rectángulos, pero no se aplica a otros tipos de triángulos, por lo que es importante distinguir el tipo de triángulo antes de utilizarlo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)