SKL (1) | Penurunan Tekanan Uap (∆P) | Kimia Kelas 12
Summary
TLDRThis educational video script introduces the concept of colligative properties of solutions, focusing on the first property—reduction in vapor pressure (ΔP). It explains how the presence of solute in a solution decreases its vapor pressure compared to the pure solvent. The script covers the calculation of ΔP using Raoult's Law for both non-electrolyte and electrolyte solutions, providing formulas and examples to illustrate the concepts. It also discusses the significance of vapor pressure in determining the ease of evaporation, with higher vapor pressures indicating greater volatility.
Takeaways
- 📚 The video is an educational tutorial on colligative properties of solutions, specifically for 12th-grade chemistry students in their first semester.
- 🔍 It emphasizes the importance of understanding the difference between electrolyte and non-electrolyte solutions before studying colligative properties.
- 🌡 Colligative properties depend on the number of solute particles in a solution, not the nature of the solute itself.
- 💧 There are four main colligative properties: lowering of vapor pressure (ΔP), elevation of boiling point (ΔTB), depression of freezing point (ΔTF), and osmotic pressure (V).
- 🌫 The video focuses on the first colligative property, the lowering of vapor pressure, denoted by ΔP.
- 🌡️ Vapor pressure indicates the tendency of a liquid to evaporate; a higher vapor pressure means the liquid evaporates more readily.
- 🔍 The presence of a solute in a solution lowers the vapor pressure compared to the pure solvent, making the solution less likely to evaporate.
- 📉 The formula ΔP = P₀ - P is used to calculate the decrease in vapor pressure, where P₀ is the vapor pressure of the pure solvent and P is the vapor pressure of the solution.
- ⚗ The formula ΔP = P₀ * (mol solute / (mol solute + mol solvent)) can be used to determine the decrease in vapor pressure for non-electrolyte solutions.
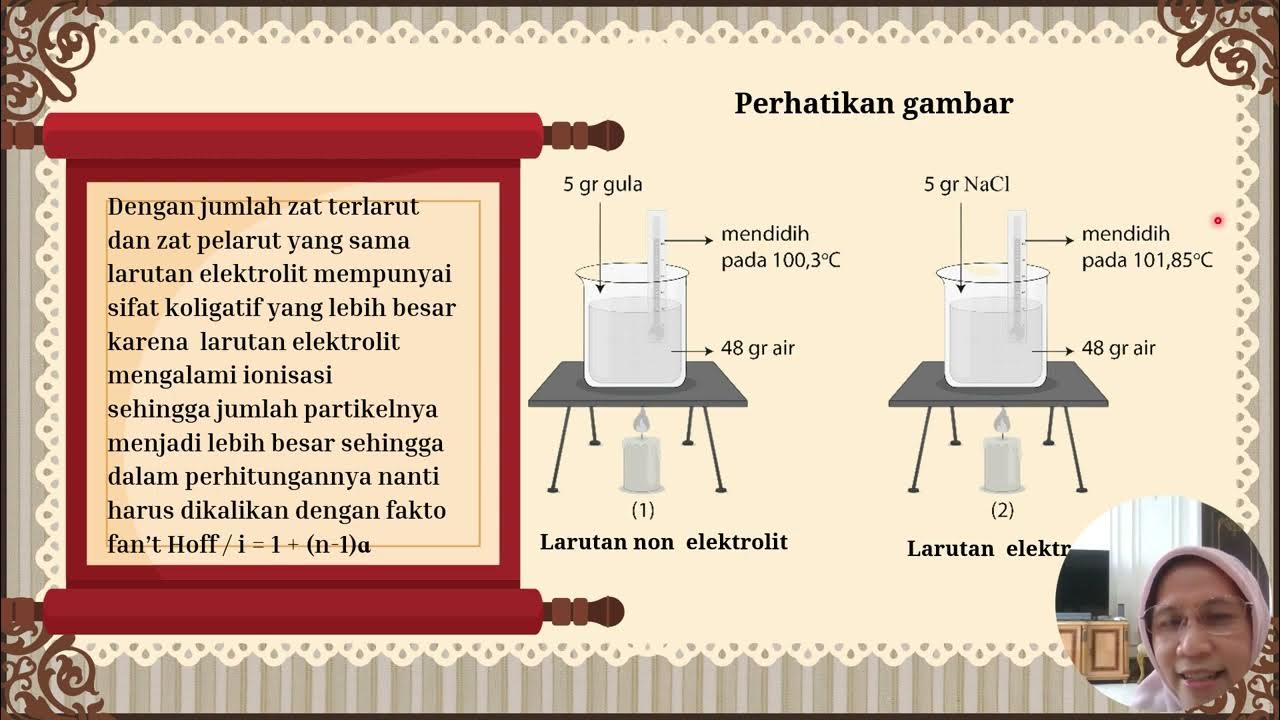
- 🔌 For electrolyte solutions, the formula for ΔP is adjusted to account for the ions produced upon dissociation, considering the van't Hoff factor (i).
- 🌡️ The van't Hoff factor (i) is calculated using the formula i = 1 + n(α - 1), where n is the number of ions and α is the degree of dissociation.
- 📝 The tutorial includes examples to illustrate the calculation of vapor pressure and ΔP for both non-electrolyte and electrolyte solutions.
Q & A
What is the main topic of the video?
-The main topic of the video is the study of colligative properties of solutions, specifically focusing on the first property, which is the lowering of vapor pressure (ΔP).
What are the prerequisites for understanding colligative properties of solutions?
-To understand colligative properties, one must first understand what a solution is, the difference between electrolytic and non-electrolytic solutions, and the units of concentration. These topics were previously studied in grade 10.
What are the four colligative properties mentioned in the script?
-The four colligative properties mentioned are: 1) lowering of vapor pressure (ΔP), 2) elevation of boiling point (ΔTB), 3) depression of freezing point (ΔTF), and 4) osmotic pressure (V).
What is the significance of vapor pressure in the context of the script?
-Vapor pressure indicates the tendency of a liquid to evaporate. A high vapor pressure suggests that a substance or liquid is more likely to evaporate, while a low vapor pressure indicates the opposite.
Why does the presence of a solute in a solution lower the vapor pressure compared to the pure solvent?
-The presence of a solute in a solution lowers the vapor pressure because the solute particles occupy some of the surface area of the solvent, making it more difficult for the solvent to evaporate.
How can the lowering of vapor pressure (ΔP) be calculated for a non-electrolytic solution?
-For a non-electrolytic solution, ΔP can be calculated using the formula ΔP = P₀ * (mol solute / (mol solute + mol solvent)), where P₀ is the vapor pressure of the pure solvent, and mol solute and mol solvent are the moles of solute and solvent, respectively.
What is the difference between calculating ΔP for a non-electrolytic solution and an electrolytic solution?
-For an electrolytic solution, the formula for ΔP is more complex, taking into account the number of ions produced upon dissociation. The formula is ΔP = P₀ * (mol solute * I) / (mol solute + mol solvent), where I is the van't Hoff factor, which is the number of ions per formula unit of the solute.
What is the van't Hoff factor and how is it determined?
-The van't Hoff factor (I) is a measure of the number of ions produced when an electrolyte dissolves in a solution. It is determined using the formula I = 1 + n * (α - 1), where n is the number of ions and α is the degree of dissociation.
How can the vapor pressure of a solution (P) be calculated for an electrolytic solution?
-For an electrolytic solution, the vapor pressure (P) can be calculated using the formula P = P₀ * (NP + nI) / (NP + n), where P₀ is the vapor pressure of the pure solvent, NP is the number of moles of solvent, n is the number of moles of solute, and I is the van't Hoff factor.
Can you provide an example calculation from the script for the lowering of vapor pressure in a solution?
-Yes, an example in the script calculates the lowering of vapor pressure when 18 grams of glucose (with a molar mass of 180 g/mol) are dissolved in 90 grams of water (with a molar mass of 18 g/mol). The calculation uses the formula ΔP = P₀ * (mol solute / (mol solute + mol solvent)) and results in a ΔP of 0.47 mmHg.
What is the final example in the script about calculating the vapor pressure of a solution?
-The final example in the script involves calculating the vapor pressure of a solution made by dissolving 1 mole of Na2SO4 in 900 grams of water at 30°C. The calculation uses the formula for electrolytic solutions and results in a vapor pressure of 30 mmHg for the solution.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Simplest Way To Understand Boiling Point Elevation & Vapor Pressure Depression
Sifat Koligatif 2Penurunan Tekanan Uap

Propriedades Coligativas - Brasil Escola

SIFAT KOLIGATIF LARUTAN - KIMIA - MATERI UTBK SBMPTN DAN SIMAK UI

الخواص الجامعة للمحاليل كيمياء ثالث ثانوي 1445

13.2 Colligative Properties of Solutions (1/2)
5.0 / 5 (0 votes)