Cambio de Bases | Esencia del álgebra lineal, capítulo 09
Summary
TLDREl guion del video explica cómo describir un vector en un espacio 2D utilizando coordenadas y escalares. Se introduce la idea de sistemas de coordenadas y vectores base, ejemplificando con dos sistemas diferentes: uno estándar y otro alternativo propuesto por 'Jennifer'. Se discute cómo traducir entre sistemas de coordenadas utilizando matrices de cambio de base y multiplicación matriz-vector. El video también explora la representación de transformaciones lineales como rotaciones y cómo estas se aplican en diferentes sistemas de coordenadas, enfatizando la importancia de la multiplicación de matrices para la composición de transformaciones.
Takeaways
- 📏 El script habla sobre cómo describir un vector en un espacio 2D utilizando coordenadas.
- 🔍 Se menciona que las coordenadas son una forma de describir el movimiento de un vector en términos de escala y dirección.
- 📚 Se introduce el concepto de vectores base y su importancia en el sistema de coordenadas estándar.
- 🎯 Se describe cómo diferentes sistemas de coordenadas pueden tener vectores base diferentes, lo que afecta la forma en que se describen los vectores.
- 🤔 Se plantea la idea de la transformación de vectores entre sistemas de coordenadas usando matrices de cambio de base.
- 📐 Se discute cómo la elección de vectores base afecta la representación de las coordenadas en un espacio 2D.
- 🧩 Se explica que la multiplicación de matrices corresponde a la composición de transformaciones y cómo se puede utilizar para traducir entre sistemas de coordenadas.
- 🔄 Se menciona la inversa de una matriz de cambio de base y su papel en la traducción de vectores de un sistema a otro.
- 📈 Se da un ejemplo de cómo calcular las coordenadas de un vector en un sistema de coordenadas dado las coordenadas en otro sistema.
- 🌐 Se destaca la importancia de comprender la multiplicación de matrices y la representación de transformaciones para entender la traducción de vectores entre sistemas de coordenadas.
Q & A
¿Qué significa que un vector tenga coordenadas 3 2 en un espacio 2D?
-Las coordenadas 3 2 indican que para ir de la cola al punto final del vector, se debe moverse 3 unidades a la derecha y 2 unidades hacia arriba en el espacio 2D.
¿Cómo se describen las coordenadas de un vector en términos de álgebra lineal?
-En álgebra lineal, las coordenadas de un vector se consideran como escalares que estiran o comprimen vectores unitarios. La primera coordenada es un escalar multiplicado por el vector unitario en dirección horizontal, y la segunda coordenada es un escalar multiplicado por el vector unitario en dirección vertical.
¿Qué son los vectores de la base en un sistema de coordenadas y por qué son importantes?
-Los vectores de la base son vectores especiales que encapsulan las suposiciones implícitas de un sistema de coordenadas. Sirven para escalar y traducir entre vectores y conjuntos de números, lo que permite la descripción de cualquier vector en el espacio usando solo números.
¿Qué es un sistema de coordenadas y cómo se relaciona con los vectores de la base?
-Un sistema de coordenadas es una forma de describir la posición de un punto en el espacio usando un conjunto de números. Los vectores de la base son los vectores que se escalan para representar cualquier otro vector en ese espacio según ese sistema.
¿Cómo se describe un vector usando un sistema de coordenadas con base diferente?
-Se describe un vector multiplicando cada uno de los vectores de la nueva base por las coordenadas correspondientes y sumando los resultados. Esto da una representación del vector en el nuevo sistema de coordenadas.
¿Por qué pueden ser diferentes las coordenadas de un mismo vector en sistemas de coordenadas diferentes?
-Las coordenadas de un vector varían según el sistema de coordenadas porque cada sistema tiene su propia base de vectores. Las coordenadas son el resultado de la proyección del vector sobre los vectores de la base de ese sistema.
¿Cómo se traducen las coordenadas de un vector de un sistema de coordenadas a otro?
-Para traducir las coordenadas de un vector de un sistema a otro, se utiliza una matriz de cambio de base que relaciona los vectores de la base de un sistema con los del otro. Se multiplica esta matriz por el vector en el sistema original para obtener las coordenadas en el nuevo sistema.
¿Qué es la multiplicación matriz-vector y cómo se relaciona con la traducción de vectores entre sistemas de coordenadas?
-La multiplicación matriz-vector es una operación que se utiliza para aplicar una transformación lineal a un vector. En el contexto de la traducción de vectores entre sistemas de coordenadas, esta operación se utiliza para convertir las coordenadas de un vector de un sistema a otro mediante una matriz de cambio de base.
¿Cómo se calcula la inversa de una matriz de cambio de base y por qué es importante?
-La inversa de una matriz de cambio de base se calcula usando el método estándar para encontrar la inversa de una matriz. Es importante porque permite traducir vectores de un sistema de coordenadas a otro, y viceversa, permitiendo la comunicación entre diferentes sistemas de coordenadas.
¿Por qué es útil el concepto de sistemas de coordenadas alternativos en álgebra lineal?
-Los sistemas de coordenadas alternativos son útiles porque permiten entender y aplicar transformaciones en diferentes referencias. Son fundamentales para el estudio de vectores propios, valores propios y para entender cómo se ven las mismas transformaciones desde diferentes perspectivas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

38 - Introducción a los Tensores

Multiplicando un vector por un escalar

Combinaciones lineales, subespacio generado y bases | Esencia del álgebra lineal, capítulo 2
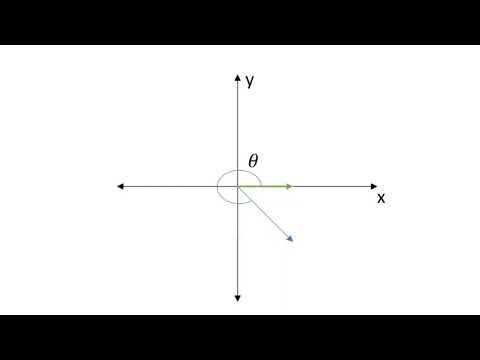
11. Vectores Clase No 3: Componentes rectangulares de un vector
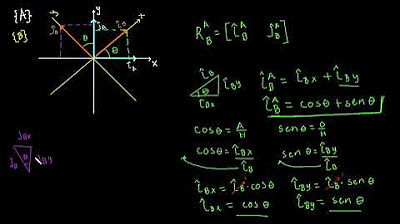
Matriz de rotación en 2d y sistemas de coordenadas

Vector posición y trayectoria | | UPV
5.0 / 5 (0 votes)
