PERSAMAAN STANDAR LINGKARAN | GEOMETRI ANALITIK

Summary

In this tutorial on analytical geometry, the instructor explains the standard equation of a circle, starting with the basic definition and key components: the center and the radius. The video covers two types of circle equations: one with a center at the origin and the other with a center at a point outside the origin. Through multiple examples, the instructor demonstrates how to derive the equation of a circle given different conditions such as the center, radius, and tangency to a line. The tutorial offers clear, step-by-step guidance on calculating and understanding circle equations in various geometric contexts.

Takeaways

• 😀 A circle is the locus of points in a plane that are equidistant from a fixed center point.
• 😀 The two most important components of a circle are its center and its radius.
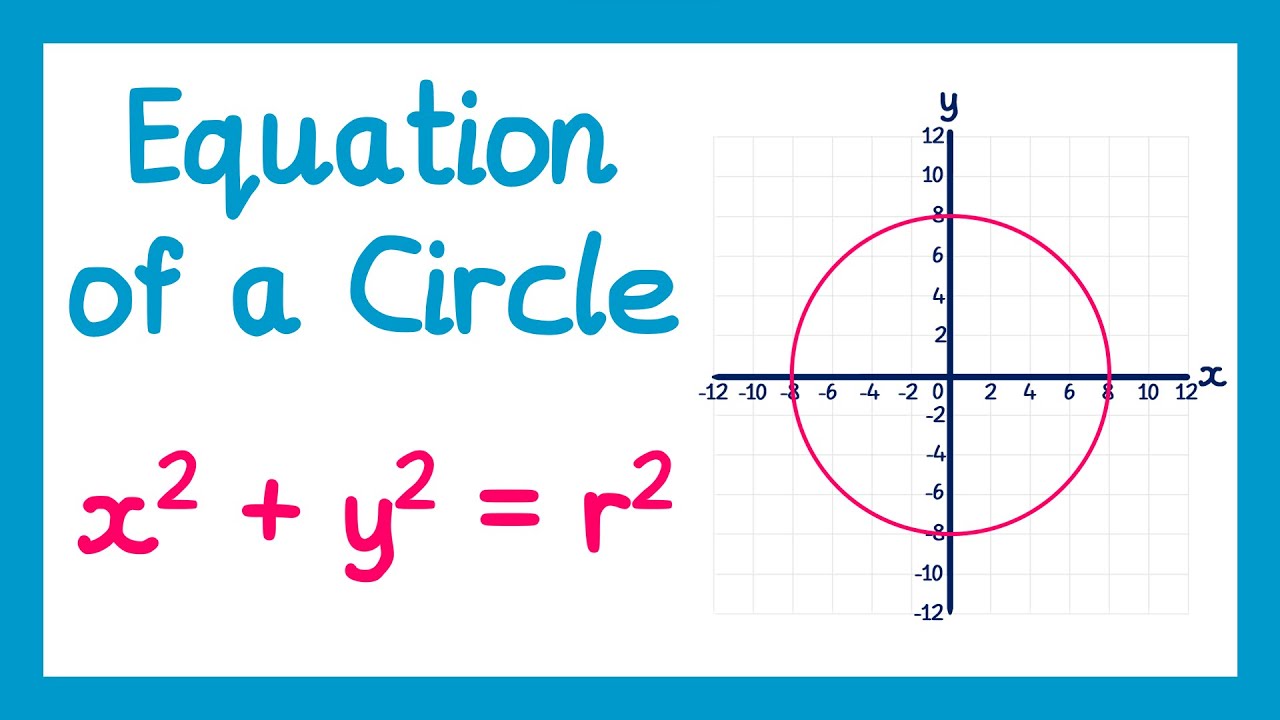
• 😀 The standard equation of a circle with center at (0,0) is x² + y² = r².
• 😀 For a circle with center at (h, k), the general equation is (x - h)² + (y - k)² = r².
• 😀 To find the equation of a circle, substitute the center coordinates and the radius into the general formula.
• 😀 The distance between two points can be used to determine the radius of a circle when given a point on the circle.
• 😀 To derive the equation of a circle, the center and radius must be known, and these values are directly plugged into the formula.
• 😀 In cases where the center is not at the origin, the equation of the circle is adjusted accordingly with (x - h)² + (y - k)² = r².
• 😀 If given the equation of a circle, the center and radius can be extracted by comparing the equation to the general form.
• 😀 The distance between a point and a line can be used to determine the radius when a circle is tangent to a line.
• 😀 The midpoint formula can be used to find the center of a circle when the endpoints of the diameter are given.

Q & A

What is the definition of a circle in analytical geometry?

A circle is the locus of points in a plane such that each point is equidistant from a fixed point called the center. The distance from the center to any point on the circle is the radius.

What are the two most important components of a circle?

The two most important components of a circle are the center and the radius. The center is a fixed point inside the circle, and the radius is the distance from the center to any point on the circle.

What is the standard equation of a circle when the center is at (0, 0)?

The standard equation of a circle with the center at (0, 0) is x² + y² = r², where r is the radius of the circle.

How is the general equation of a circle represented when the center is at (h, k)?

The general equation of a circle with center at (h, k) and radius r is (x - h)² + (y - k)² = r².

What is the purpose of using the distance formula in circle equations?

The distance formula is used to calculate the distance between the center and any point on the circle, which gives the radius. This helps derive the equation of the circle.

How do you find the equation of a circle when the center and radius are known?

To find the equation of a circle when the center is (h, k) and the radius is r, use the formula: (x - h)² + (y - k)² = r².

What is the significance of the equation x + 2² + y - 3² = 4?

This is the equation of a circle with center at (-2, 3) and radius 2. It is written in standard form as (x + 2)² + (y - 3)² = 4.

How can you determine the center and radius of a circle from its equation?

From the equation of a circle, the center can be found as (h, k) by observing the terms (x - h) and (y - k). The radius is the square root of the constant on the right-hand side of the equation.

How do you find the radius of a circle when given a point on the circle and its center?

The radius can be found using the distance formula between the center and the given point on the circle. The distance formula is: r = √((x2 - x1)² + (y2 - y1)²).

What method is used to find the equation of a circle that is tangent to a line?

To find the equation of a circle tangent to a line, first determine the distance from the center of the circle to the line, which will be equal to the radius. Then, use the general circle equation with the center and radius.