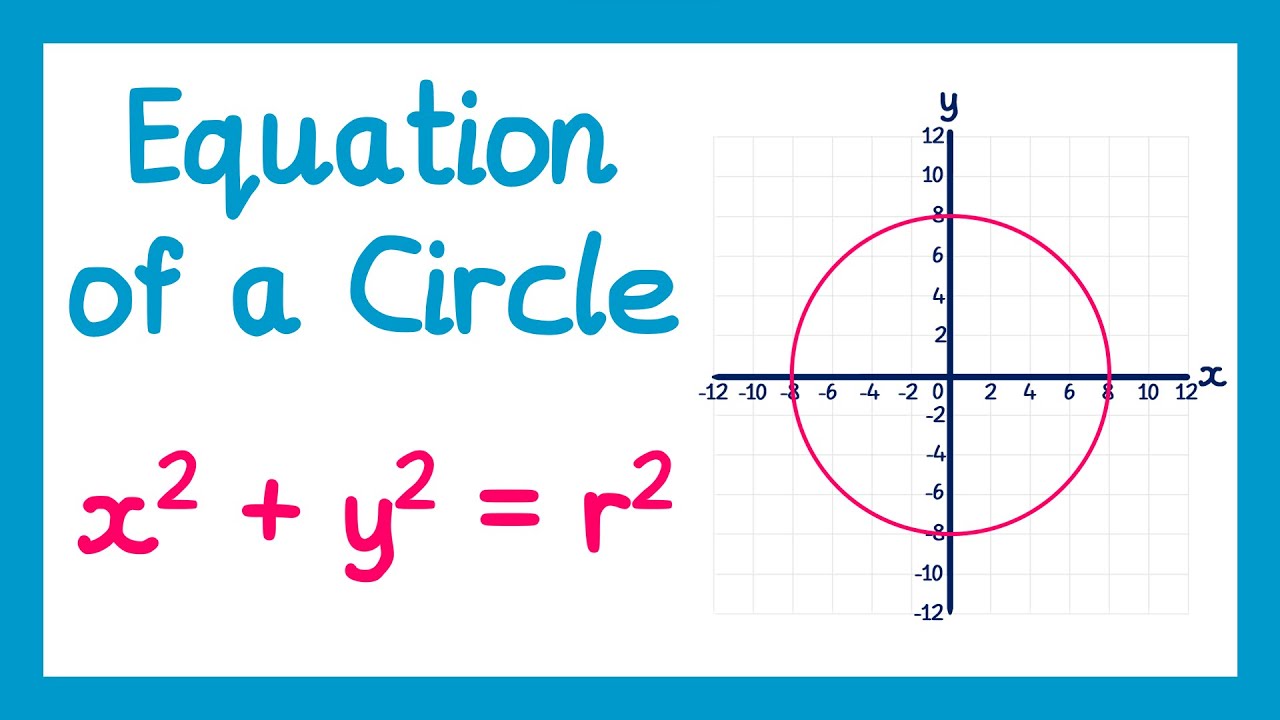
Persamaan Lingkaran Pusat (0, 0) dan jari jari r

Summary

In this video, Asmara Ahmad explains the equation of a circle centered at the origin (0,0) with radius R. The tutorial begins with the basic concepts of circles learned in middle school, like calculating area and circumference, before advancing to analytical geometry for high school. Through examples, viewers learn how to derive the equation of a circle, using the Pythagorean theorem and simple algebraic substitutions. The video also covers methods for determining the radius of a circle from its equation and explores various problems involving circles, including finding the equation for a circle passing through specific points or tangent to a line.

Takeaways

• 😀 The video introduces the topic of the equation of a circle with center at the origin (0,0) and radius R.
• 😀 In middle school, we learn to calculate the area and circumference of a circle, while high school focuses on analytic geometry and determining the equation of a circle.
• 😀 The equation of a circle centered at (0,0) is derived using the Pythagorean theorem, resulting in the formula: x² + y² = r².
• 😀 The derivation of the circle's equation involves considering a random point on the circle, applying the Pythagorean theorem to form the equation.
• 😀 An example is provided where the radius is 9, yielding the equation x² + y² = 81.
• 😀 Another example with a radius of 3√2 results in the equation x² + y² = 18.
• 😀 A third example involves determining the radius of a circle given its equation x² + y² = 121, with the radius being 11.
• 😀 For a circle with the equation x² + y² = 200, the radius is calculated as 10√2.
• 😀 A problem is discussed where the equation of a circle with center at (0,0) passes through a given point (-5,12). The radius is calculated using the distance formula, resulting in a radius of 13.
• 😀 Another example demonstrates finding the equation of a circle with center at (0,0) that is tangent to a line 3x - 4y + 15 = 0. The radius is calculated as 3, and the resulting equation of the circle is x² + y² = 9.

Q & A

What is the general equation of a circle centered at the origin (0, 0)?

The general equation of a circle centered at the origin is x^2 + y^2 = r^2, where r is the radius of the circle.

How do we derive the equation of a circle from the Pythagorean theorem?

By using the Pythagorean theorem, we consider a right triangle formed by the radius of the circle and the x and y coordinates of a point on the circle. The Pythagorean theorem gives us the relation x^2 + y^2 = r^2.

What does the variable 'r' represent in the equation of a circle?

'r' represents the radius of the circle, which is the distance from the center (0, 0) to any point on the circle.

Why is the absolute value of x and y used in the derivation of the equation of a circle?

The absolute values of x and y are used to account for all possible points on the circle in all quadrants, ensuring the equation holds true for any point on the circle.

How do we calculate the equation of a circle when the radius is given, for example, r = 9?

If the radius is 9, we substitute r = 9 into the general equation x^2 + y^2 = r^2, which gives x^2 + y^2 = 81.

What is the relationship between the equation x^2 + y^2 = 121 and the radius of the circle?

In the equation x^2 + y^2 = 121, the value 121 represents r^2, so the radius r is the square root of 121, which is 11.

How do you determine the radius of a circle if the equation is x^2 + y^2 = 200?

To find the radius, take the square root of 200, which simplifies to 10√2. Therefore, the radius is 10√2.

What should we do when given a circle passing through a specific point, such as (-5, 12)?

To find the equation of the circle passing through (-5, 12), substitute the coordinates of the point into the equation x^2 + y^2 = r^2, then solve for r.

How do you calculate the radius when the center of the circle is at the origin and the circle passes through a point like (-5, 12)?

To calculate the radius, use the distance formula between the center (0, 0) and the point (-5, 12). The distance is √((-5)^2 + 12^2), which gives √169 = 13. Therefore, the radius is 13.

What is the significance of a line being tangent to a circle in relation to finding its equation?

A tangent line touches the circle at exactly one point, and the distance from the center of the circle to the tangent line is equal to the radius. This relationship is used to determine the equation of the circle when the line is given.