Equation of a Circle

Summary

This video explains the equation of a circle, starting with the basic form x² + y² = r² for a circle centered at the origin. It covers how the equation changes when the center is shifted and demonstrates various examples, including finding the equation of a circle given its center and radius. The video also tackles solving problems involving points on the circle, calculating the radius, and determining the equation of a tangent. By using clear visuals and examples, the video provides a solid understanding of circle equations and their practical applications in geometry.

Takeaways

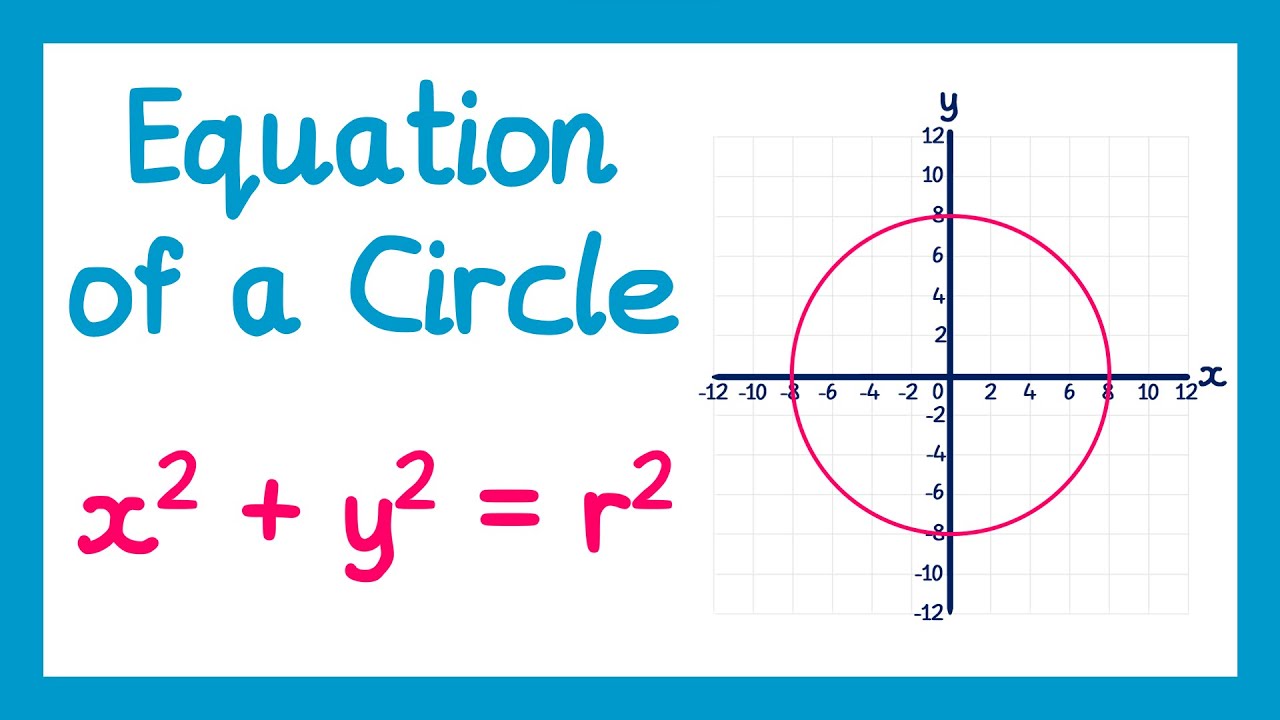
• 😀 The equation of a circle is given by x² + y² = r², where the center is at (0, 0) and the radius is r.
• 😀 When the center of a circle is not at the origin, the equation changes to (x - a)² + (y - b)² = r², where (a, b) are the new coordinates of the center.
• 😀 The general form of a circle's equation is (x - a)² + (y - b)² = r², where (a, b) is the center and r is the radius.
• 😀 For a circle with center at (2, 3) and radius 3, the equation becomes (x - 2)² + (y - 3)² = 9.
• 😀 To find the equation of a circle, you need the center's coordinates and the radius, and apply the general formula.
• 😀 The radius of a circle can be found by substituting a known point on the circle into the equation and solving for r.
• 😀 If the center is (a, b) and the radius is r, the equation of the circle is (x - a)² + (y - b)² = r², with the opposite signs for a and b.
• 😀 If you're given the center and a point on the circle, you can use the distance formula to find the radius and write the circle's equation.
• 😀 The midpoint of the diameter of a circle gives the center of the circle. The radius is half the length of the diameter.
• 😀 To find the equation of a tangent to a circle at a given point, you need the gradient of the radius and use the negative reciprocal for the tangent's gradient.

Q & A

What is the general equation of a circle?

The general equation of a circle is (x - a)² + (y - b)² = r², where (a, b) represents the center of the circle, and r is the radius.

How does the equation of a circle change when the center is moved?

When the center of the circle is moved, the equation changes based on the new center coordinates. For a circle with center (a, b), the equation becomes (x - a)² + (y - b)² = r², where r is the radius.

How do you write the equation of a circle with center (2, 3) and radius 3?

The equation of a circle with center (2, 3) and radius 3 would be (x - 2)² + (y - 3)² = 9.

What happens to the equation when the radius of the circle changes?

When the radius changes, the value on the right-hand side of the equation changes. If the radius becomes r, the equation becomes (x - a)² + (y - b)² = r².

How do you determine the equation of a circle if the center is (2, 1) and the radius is 4?

The equation of the circle would be (x - 2)² + (y - 1)² = 16, because 4² = 16.

What is the equation of a circle with center (-4, 3) and radius 2?

The equation of the circle is (x + 4)² + (y - 3)² = 4, because the radius squared is 2² = 4.

How do you derive the equation of a circle from its general form if you know the center and a point on the circle?

To derive the equation, substitute the coordinates of the point on the circle into the equation (x - a)² + (y - b)² = r² to solve for r, the radius. Then write the final equation with the determined radius.

Given the center (1, -3) and a point on the circle (7, -11), how do you find the equation of the circle?

Substitute the point (7, -11) into the equation (x - 1)² + (y + 3)² = r². Solve for r²: (7 - 1)² + (-11 + 3)² = 36 + 64 = 100. Therefore, the equation is (x - 1)² + (y + 3)² = 100.

How do you find the equation of a circle when you're given the diameter and two points on the diameter?

Find the center by calculating the midpoint of the two points, then find the radius by calculating the distance from the center to either point on the diameter. Use these to write the equation of the circle.

How do you find the tangent to a circle at a given point?

To find the tangent, first calculate the gradient of the radius at the point of tangency. The gradient of the tangent is the negative reciprocal of the gradient of the radius. Then, use the point-slope form of the equation of a line to write the equation of the tangent.