Laws of Radicals | Math Mondays

Summary

In this educational video, the speaker breaks down the four laws of radicals, explaining how to simplify and manipulate radical expressions. The content covers the laws of exponents, simplifying square roots, cube roots, and other radical forms, with practical examples and step-by-step instructions. Key concepts include splitting numbers, using variables, and handling fractions within radicals. The video concludes with a quiz to test understanding, encouraging viewers to apply the learned laws. The speaker also promotes further engagement through social media and merchandise to support the channel.

Takeaways

• 😀 The video focuses on explaining the laws of radicals and exponents.
• 😀 The first law of radicals involves raising a radicand to an exponent, simplifying the expression by following the format of the index and exponent.
• 😀 Example for the first law: The square root of 16 raised to the power of 2 simplifies to 16.
• 😀 Law number two involves splitting a radical expression into smaller factors for simplification, like breaking down the square root of 36 into the square roots of 9 and 4.
• 😀 Perfect square numbers (like 9 and 4) can be simplified directly into their integer square roots (e.g., √9 = 3 and √4 = 2).
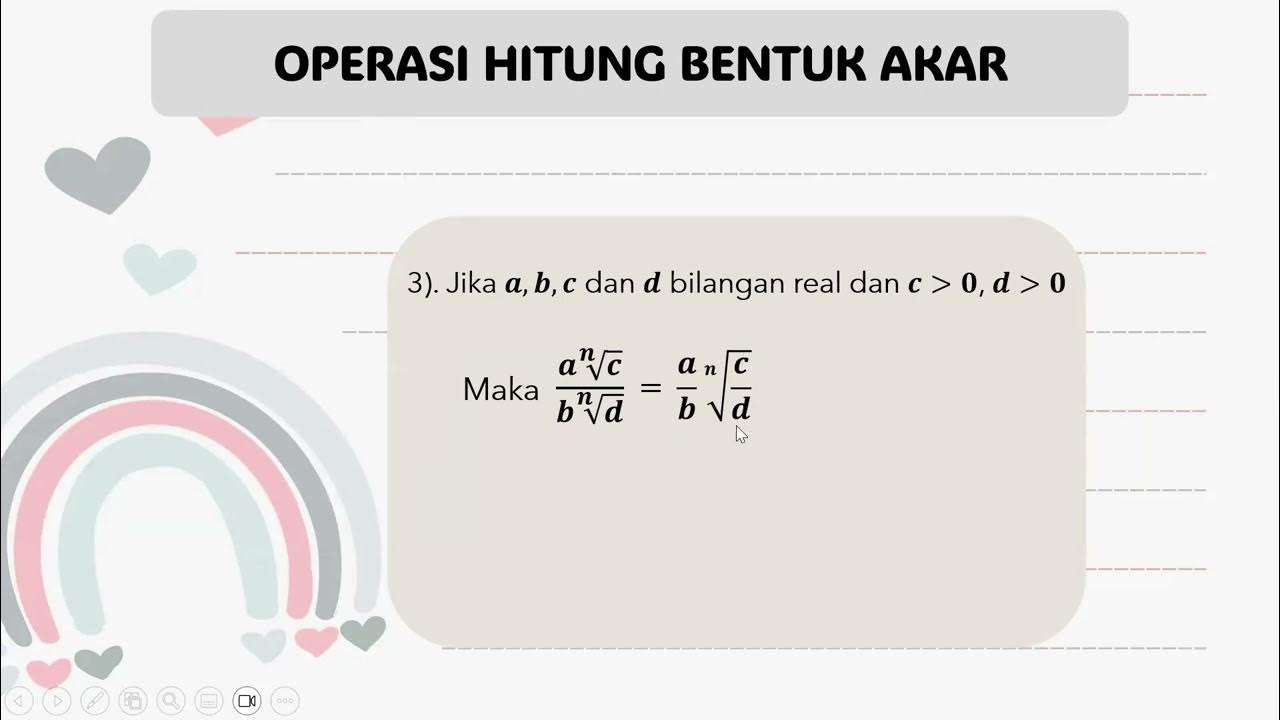
• 😀 Law number three explains how to deal with fractions under radicals by splitting the numerator and denominator and simplifying them separately.
• 😀 Example of law three: The cube root of 8/27 can be simplified to 2/3.
• 😀 Law number four illustrates how to simplify radical expressions with variables, like simplifying expressions involving x and y under square roots.
• 😀 Law number four example: The fourth root of 16x⁴ simplifies to 2x, where the radicand (16) and the variable (x⁴) are simplified separately.
• 😀 The importance of mastering these laws is highlighted, as they allow you to simplify complex radical expressions and make solving algebraic problems easier.
• 😀 The video ends with a brief quiz to test understanding of the laws and encourages further practice on social media platforms.

Q & A

What is the first law of radicals mentioned in the script?

The first law states that when a number under a radical is raised to the power of the index, the answer is simply the radicand (the number under the radical symbol). For example, the square root of 16 raised to the power of 2 equals 16.

How can we simplify the square root of 16 raised to the power of 2?

We can first find the square root of 16, which is 4. Then, raise 4 to the power of 2, which gives us 16. This is an example of applying the first law of radicals.

What does the second law of radicals involve?

The second law involves splitting the radical into separate parts when the number inside the radical is a product. For example, the square root of 36 can be split into the square root of 9 and the square root of 4, both of which are perfect squares and simplify to 3 and 2, respectively. The final answer is 6.

How do we handle variables in radicals according to the second law?

For example, the square root of 4x can be split into the square root of 4 and the square root of x. The square root of 4 is 2, and the square root of x is simply x. Thus, the answer is 2x.

What is the third law of radicals about?

The third law of radicals explains how to simplify fractions under a radical. For example, the cube root of 8/27 can be split into the cube root of 8 and the cube root of 27, which simplifies to 2/3 because both 8 and 27 are perfect cubes.

How would we simplify a radical like the cube root of 8y cubed?

We can split it into the cube root of 8 and the cube root of y cubed. The cube root of 8 is 2, and the cube root of y cubed is simply y. Therefore, the final answer is 2y.

What does the fourth law of radicals describe?

The fourth law of radicals is about simplifying expressions that involve higher powers. For example, the fourth root of 16x to the power of 4 can be split into the fourth root of 16 and the fourth root of x to the power of 4. The fourth root of 16 is 2, and the fourth root of x to the power of 4 is x. Thus, the answer is 2x.

How do you solve an expression like the square root of 100 over 25?

You can split it into the square root of 100 and the square root of 25. The square root of 100 is 10, and the square root of 25 is 5. Therefore, the final answer is 10/5, which simplifies to 2.

What is the correct approach to handling an expression like x² under the square root over the square root of 4y⁴?

This expression can be split into the square root of x² and the square root of 4y⁴. The square root of x² is x, and the square root of 4y⁴ is 2y². Therefore, the answer is x over 2y².

How is the final answer calculated for an expression involving the multiplication of index numbers, such as the fourth root of 16 times x⁴?

We can split the expression into the fourth root of 16 and the fourth root of x⁴. The fourth root of 16 is 2, and the fourth root of x⁴ is x. Thus, the final answer is 2x.