Probabilitas dan Statistik: 8.6 Central Limit Theorem

Summary

This video explains the concept of the Central Limit Theorem (CLT) in probability and statistics, focusing on the sampling distribution of the sample mean. It covers how, as the sample size increases, the distribution of sample means approaches a normal distribution, regardless of the population's original distribution. The video discusses practical applications of the CLT in statistical inference, such as hypothesis testing and estimation. Key takeaways include the importance of a sufficiently large sample size (usually 25-40) to apply CLT and how this theorem bridges probability and statistics for making population-level decisions from samples.

Takeaways

• 😀 The Central Limit Theorem (CLT) explains the distribution of sample means as sample size increases, converging towards a normal distribution.
• 😀 CLT applies regardless of the population's original distribution, as long as the sample size is sufficiently large (typically n ≥ 30).
• 😀 The formula for the Z-score of the sample mean is: Z = (X̄ - μ) / (σ / √n), and it tends toward a standard normal distribution as n approaches infinity.
• 😀 CLT is foundational for statistical estimation and hypothesis testing, enabling valid inferences even from non-normally distributed populations.
• 😀 Larger sample sizes improve the approximation of the sample mean distribution to a normal distribution.
• 😀 For sample sizes less than 30, the population distribution should be checked before assuming normality in the sample mean distribution.
• 😀 If a population is normally distributed, the sample mean distribution is normal for all sample sizes, not just for n ≥ 30.
• 😀 CLT bridges the gap between probability and statistics, allowing statistical inference from sample data to population parameters.
• 😀 A sample mean's distribution tends toward normality regardless of the original distribution of the population, given a large enough sample size.
• 😀 The empirical distribution shape (e.g., skewed or uniform) will result in a sample mean distribution that tends toward normal as n increases.
• 😀 The practical rule is to use sample sizes of 25-40 to apply the Central Limit Theorem effectively, ensuring a good approximation to normal distribution.

Q & A

What is the Central Limit Theorem (CLT)?

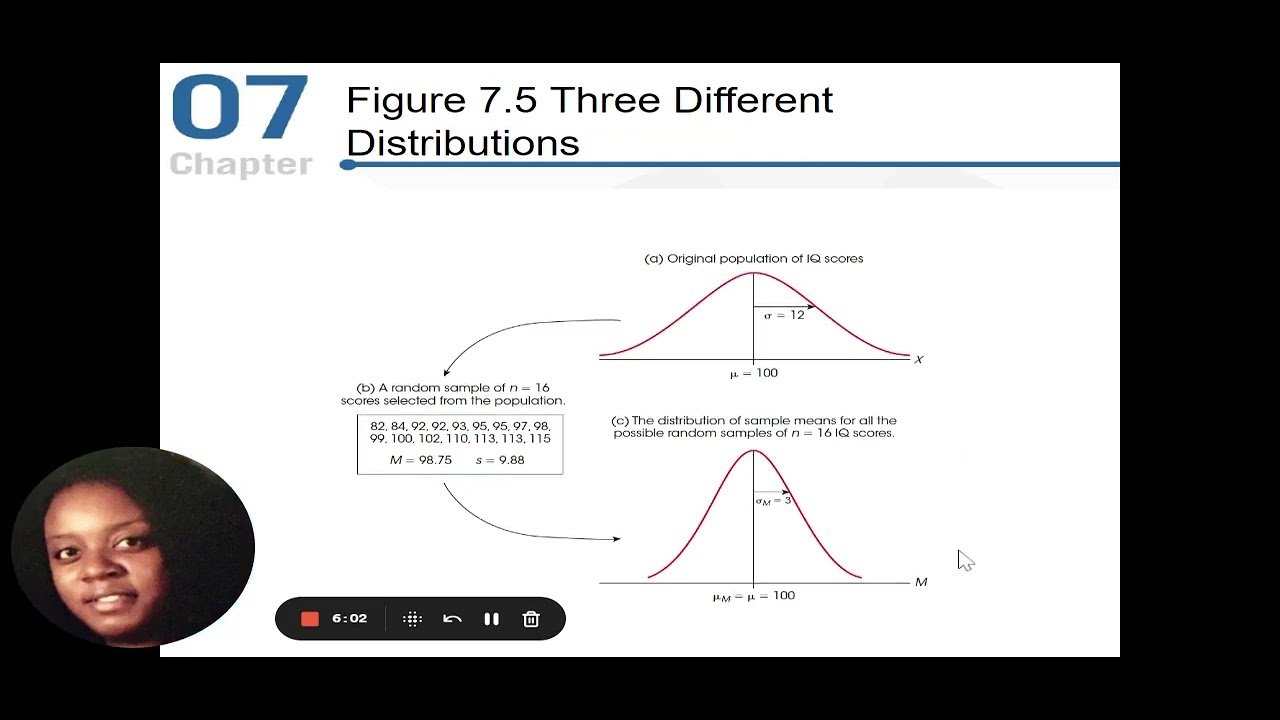
The Central Limit Theorem (CLT) states that the sampling distribution of the sample mean (X̄) will approach a normal distribution as the sample size (n) increases, regardless of the shape of the population distribution.

What happens to the sampling distribution of the sample mean as the sample size increases?

As the sample size increases, the sampling distribution of the sample mean approaches a normal distribution, even if the population distribution is not normal.

What are the key conditions for the CLT to hold?

The CLT holds when a random sample of size n is taken from any population, and as n approaches infinity, the sample mean’s distribution will become approximately normal.

How is the Z-score formula related to the Central Limit Theorem?

The Z-score formula, Z = (X̄ - μ) / (σ / √n), is used to standardize the sample mean in relation to the population mean (μ) and standard deviation (σ), and it follows a standard normal distribution as n becomes large.

What does the CLT imply for statistical inference?

The CLT allows us to use the sample mean to make inferences about the population mean, facilitating statistical estimation, hypothesis testing, and decision-making.

Is there an assumption about the distribution of the population when applying the CLT?

No, there is no assumption about the population’s distribution when applying the CLT. The theorem works regardless of the population's original distribution, as long as the sample size is sufficiently large.

What is the rule of thumb for sample size to apply the Central Limit Theorem?

A common rule of thumb is that a sample size greater than 30 is sufficient to apply the CLT and assume that the sampling distribution of the mean will be approximately normal.

What happens if the population is already normally distributed?

If the population is normally distributed, the sample mean will be normally distributed for any sample size, not just for large n (i.e., n > 30).

How does the shape of the population distribution affect the sample mean’s distribution according to the CLT?

The shape of the population distribution does not significantly affect the sample mean’s distribution when n is large. Regardless of whether the population distribution is skewed or box-shaped, the sample mean’s distribution will tend toward normality as n increases.

What are the practical implications of the Central Limit Theorem for statistical analysis?

The CLT allows statisticians to use the normal distribution as an approximation for the sample mean, which simplifies calculations for confidence intervals, hypothesis testing, and other inferential statistics, even when the underlying population is not normally distributed.