Gráfica de una función coseno con amplitud periodo y desfase ejemplo 5
Summary
TLDREn este video, se explica cómo representar una función coseno con transformaciones de amplitud, periodo y fase. Se comienza identificando los tres elementos clave: la amplitud (3), el periodo (3π) y el desplazamiento de fase (-2π/3). Luego, se traza la gráfica comenzando en x = -π y finalizando en x = 3π, dividiendo el intervalo en cuatro partes iguales. Se analiza cómo la gráfica se estira horizontal y verticalmente, comparando con la función coseno estándar. Se destacan los efectos de la transformación, mostrando cómo la gráfica cambia en amplitud, periodo y desplazamiento.
Takeaways
- 😀 La amplitud de la función es 3, lo que significa que el valor máximo es 3 y el mínimo es -3.
- 😀 El periodo de la función se calcula como 3π, que indica que la gráfica se repite cada 3π unidades en el eje x.
- 😀 La fase de la función está desplazada -2/3π, lo que significa que la gráfica se mueve π unidades hacia la derecha.
- 😀 El valor de la amplitud corresponde al número que multiplica a la función coseno, en este caso 3.
- 😀 El periodo de la función se calcula como 2π dividido por el coeficiente de x, que en este caso es 2/3, resultando en 3π.
- 😀 La fase de la función es el ángulo que se suma o resta al argumento del coseno, que en este caso es -2/3π.
- 😀 La gráfica de la función se representa dividiendo el segmento de la función en 4 partes iguales, que corresponden a los cuartos de la función.
- 😀 El primer punto de la gráfica se encuentra en el valor máximo (3), el segundo en cero, el tercero en el valor mínimo (-3), y el cuarto nuevamente en cero.
- 😀 La representación gráfica muestra cómo la función coseno estándar tiene un periodo menor (2π) y una amplitud de 1, mientras que la función modificada tiene un periodo mayor y amplitud mayor.
- 😀 La gráfica de la función modificada tiene un desplazamiento hacia la derecha en comparación con la función coseno estándar, que comienza en cero.
- 😀 La función coseno en el ejemplo tiene un comportamiento repetitivo, extendiéndose indefinidamente hacia la derecha y la izquierda.
Q & A
¿Cuál es la amplitud de la función coseno representada en el script?
-La amplitud de la función coseno representada es 3, lo que significa que el valor máximo de la función es 3 y el valor mínimo es -3.
¿Cómo se calcula el periodo de la función?
-El periodo de la función se calcula con la fórmula 2π/a, donde 'a' es el número que acompaña a la variable X. En este caso, a = 2/3, por lo que el periodo es 3π.
¿Qué es el desfase y cómo se calcula en esta función?
-El desfase es el ángulo que se suma o resta a la función coseno. En este caso, el desfase es -2π/3, lo que implica un desplazamiento hacia la derecha de la gráfica.
¿Cuál es el punto de inicio de la representación gráfica de la función?
-La gráfica de la función comienza en el punto -π, ya que el desfase es -2π/3, lo que implica un desplazamiento de π unidades hacia la derecha desde el origen (0, 0).
¿Cómo se divide el segmento para representar la función correctamente?
-El segmento entre el punto de inicio (-π) y el punto final (3π) se divide en cuatro partes iguales para representar la gráfica de la función. Esto permite calcular los puntos donde la función alcanza sus valores máximos, mínimos y cero.
¿Dónde alcanza la función coseno su valor máximo?
-La función alcanza su valor máximo en 3, lo que corresponde a la amplitud de la función. Este punto se da en el primer cuarto del segmento que se divide.
¿Qué sucede con la gráfica de la función coseno en comparación con la gráfica estándar de coseno?
-La gráfica de la función representada en el script tiene un periodo mayor (3π) en comparación con la gráfica estándar de coseno que tiene un periodo de 2π. Además, la gráfica está estirada verticalmente, ya que la amplitud es 3 en lugar de 1.
¿Cómo afecta el desfase a la gráfica de la función?
-El desfase de -2π/3 provoca un desplazamiento de la gráfica hacia la derecha, lo que significa que la función comienza en el punto -π en lugar de en el origen (0, 0).
¿Qué se observa al comparar la gráfica de la función representada con la gráfica de coseno estándar?
-Se observa que la gráfica de la función representada tiene un periodo mayor (3π en lugar de 2π), un estiramiento vertical debido a la amplitud de 3 y un desplazamiento hacia la derecha debido al desfase de -2π/3.
¿Es posible representar la función coseno hacia la izquierda y hacia la derecha de la gráfica?
-Sí, la función coseno se repite indefinidamente hacia la derecha y hacia la izquierda. La representación gráfica en el script muestra cómo se repite la función, con flechas que indican que continúa en ambas direcciones.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

GRÁFICA, AMPLITUD, PERIODO y MÁS de la funcion SENO, COSENO, TANGENTE
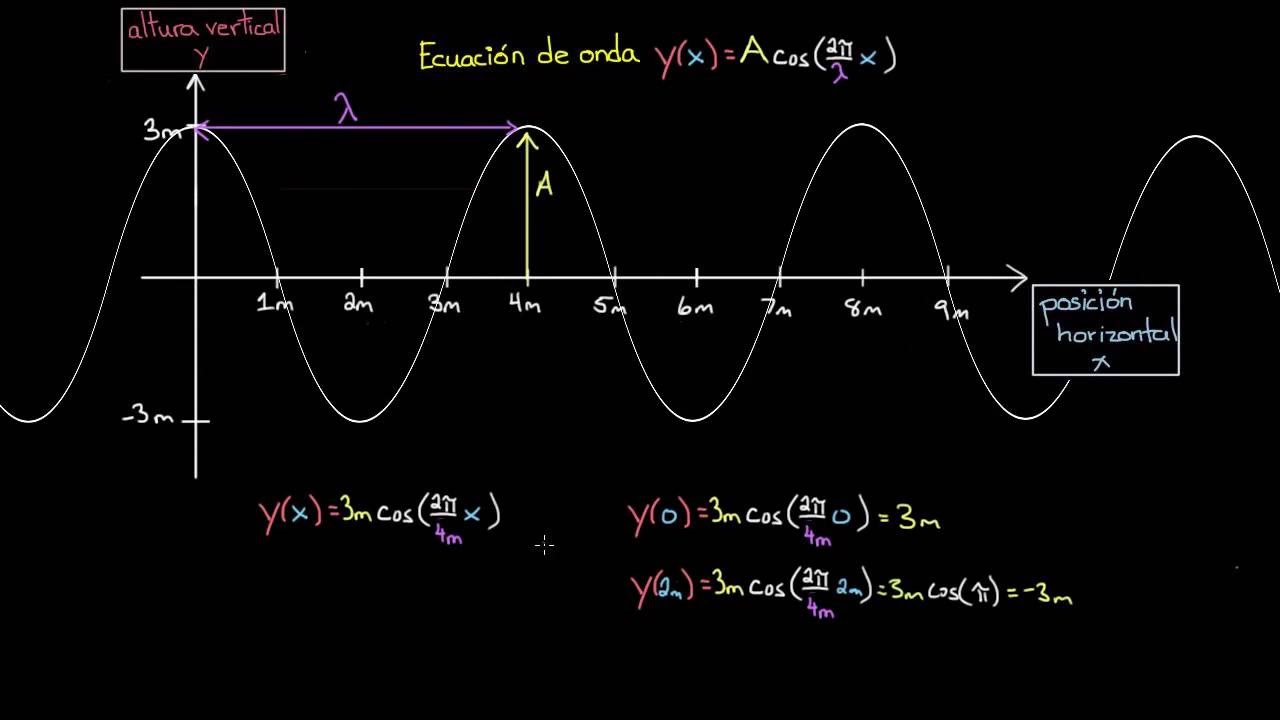
Ecuación de una onda | Física | Khan Academy en Español

Ecuaciones para osciladores armónicos simples | Física | Khan Academy en Español
Creación de una Onda con GeoGebra - Movimiento Armónico Simple

GRAFICA DE FUNCIÓN COSENO

Transformaciones de las funciones trigonométrica de seno y coseno
5.0 / 5 (0 votes)
