LEI DOS SENOS | TEOREMA DOS SENOS
Summary
TLDRThis lesson guides students through the process of solving exercises involving non-right triangles using the Law of Sines. The instructor explains how to derive the formula for the Law of Sines, focusing on non-right (acute and obtuse) triangles, and demonstrates its application in various exercises. The video emphasizes the importance of understanding triangle properties, applying sine calculations, and solving real-world problems. The lesson also includes step-by-step solutions, making it easy to grasp key concepts like sine ratios and their practical use in geometry.
Takeaways
- 😀 The Law of Sines applies to non-right triangles, allowing for the calculation of unknown sides or angles.
- 😀 The formula for the Law of Sines is: \( \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \), where a, b, c are the sides of the triangle and A, B, C are the angles.
- 😀 The Law of Sines is derived from the relationship between the sides and angles of a triangle, particularly using the definition of sine.
- 😀 The formula for sine of an angle in a triangle can be used to express relationships between sides and angles in non-right triangles.
- 😀 Using the Law of Sines, one can calculate unknown sides when two angles and one side are known (Angle-Angle-Side situation).
- 😀 The Law of Sines can also be used to solve for unknown angles in cases where two sides and a non-included angle are given (Side-Angle-Side situation).
- 😀 Cross-multiplication and division are key mathematical operations used when solving for unknowns with the Law of Sines.
- 😀 The Law of Sines helps solve real-world problems, such as finding the distance between landmarks, using maps and known angles.
- 😀 The relationship between distances on a map and real-world distances is an example of practical application of the Law of Sines.
- 😀 The instructor emphasizes practice and further application of the Law of Sines to improve understanding and solve various triangle-related problems.
Q & A
What is the Law of Sines and how is it used in solving triangles?
-The Law of Sines is a mathematical formula that relates the sides of a triangle to the sines of its angles. It is especially useful for solving non-right triangles. The law states that for any triangle, the ratio of a side to the sine of its opposite angle is constant across all three sides. This is expressed as: a/sin(A) = b/sin(B) = c/sin(C).
Why is the Law of Sines applied when solving a non-right triangle?
-The Law of Sines is applied when solving non-right triangles because, unlike right triangles, trigonometric ratios such as sine, cosine, and tangent cannot directly be used with the Pythagorean theorem. The Law of Sines allows us to relate the angles and sides of the triangle to find missing values.
What is the formula for the Law of Sines, and how is it derived?
-The formula for the Law of Sines is: a/sin(A) = b/sin(B) = c/sin(C). It is derived by considering the relationship between the sides and angles of a triangle. The process involves splitting the triangle into smaller right triangles using heights (altitudes) and applying trigonometric ratios like sine to those smaller triangles.
What is the difference between using the Law of Sines and the Law of Cosines?
-The Law of Sines is typically used when you know either two angles and one side (AAS or ASA), or two sides and a non-included angle (SSA). The Law of Cosines is used when you know two sides and the included angle (SAS), or all three sides of a triangle (SSS). The Law of Cosines is more useful for calculating angles when you do not have a right triangle.
What are the steps to derive the formula for the Law of Sines?
-To derive the Law of Sines, start by considering a triangle with known vertices and heights (altitudes). By using trigonometric ratios such as sine, you can relate the sides to the angles. The relationship between the sides and angles is derived from the sine function applied to the smaller right triangles formed by the altitudes.
How do you calculate the sine of an angle in a triangle?
-The sine of an angle in a right triangle is calculated as the ratio of the length of the side opposite the angle to the length of the hypotenuse. For example, in a right triangle with angle B, the sine of angle B is given by: sin(B) = opposite side / hypotenuse.
Why is the sine of 30 degrees equal to 0.5?
-The sine of 30 degrees is 0.5 because, in a unit circle, the ratio of the opposite side to the hypotenuse for an angle of 30 degrees (or π/6 radians) is 1/2, hence sin(30°) = 0.5.
In the example problem, how did the Law of Sines help solve for distances?
-In the example, the Law of Sines helped solve for distances (x and y) by relating the sides of the triangle to the angles. Using the known values for angles and sides, the Law of Sines was used to form equations and solve for the unknown distances using trigonometric ratios.
How do you use the Law of Sines in real-world applications?
-The Law of Sines is used in various real-world applications like navigation, surveying, astronomy, and physics. For example, it can be used to calculate distances and angles in map-making, determine the height of tall objects using triangulation, or predict satellite movements in space.
What is the process for solving for unknown values in a triangle using the Law of Sines?
-To solve for unknown values in a triangle using the Law of Sines, identify the known angles and sides, set up ratios using the formula a/sin(A) = b/sin(B) = c/sin(C), and solve for the unknown values. If you have two known angles and one side, you can use the Law of Sines to find the remaining sides. If you have two sides and one non-included angle, you can find the angles.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Geometry 8-3: The Law of Sines
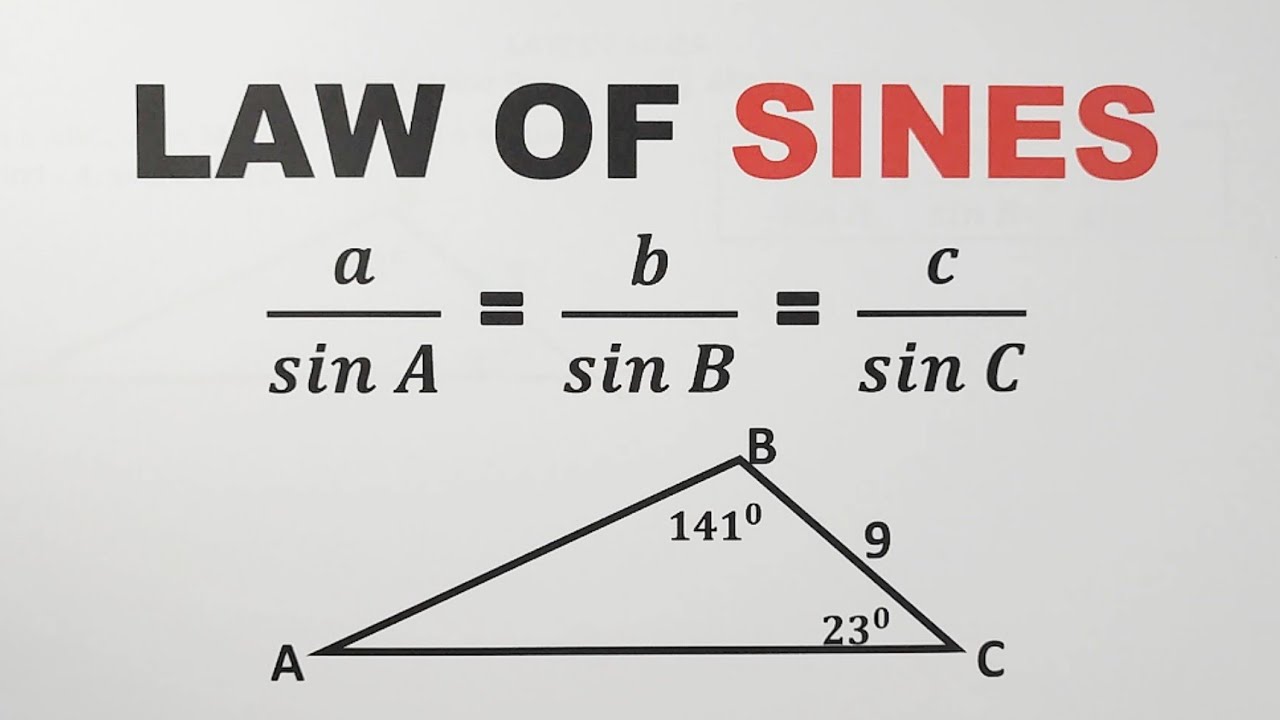
Law of Sines - Solving Oblique Triangle

Aturan Sinus dan Cosinus | Matematika SMA

SEGITIGA ISTIMEWA SUDUT 30,60,90 DAN SUDUT 45,45,90

teorema pythagoras kelas 8 "bagian 4" (mudah): menentukan perbandingan sisi-sisi segitiga siku-siku

Pembahasan Latihan 5.3 Kesebangunan Hal 179-181 Bab 5 KESEBANGUNAN kelas 7 SMP Kurikulum Merdeka
5.0 / 5 (0 votes)