Pembahasan Latihan 5.3 Kesebangunan Hal 179-181 Bab 5 KESEBANGUNAN kelas 7 SMP Kurikulum Merdeka

Summary

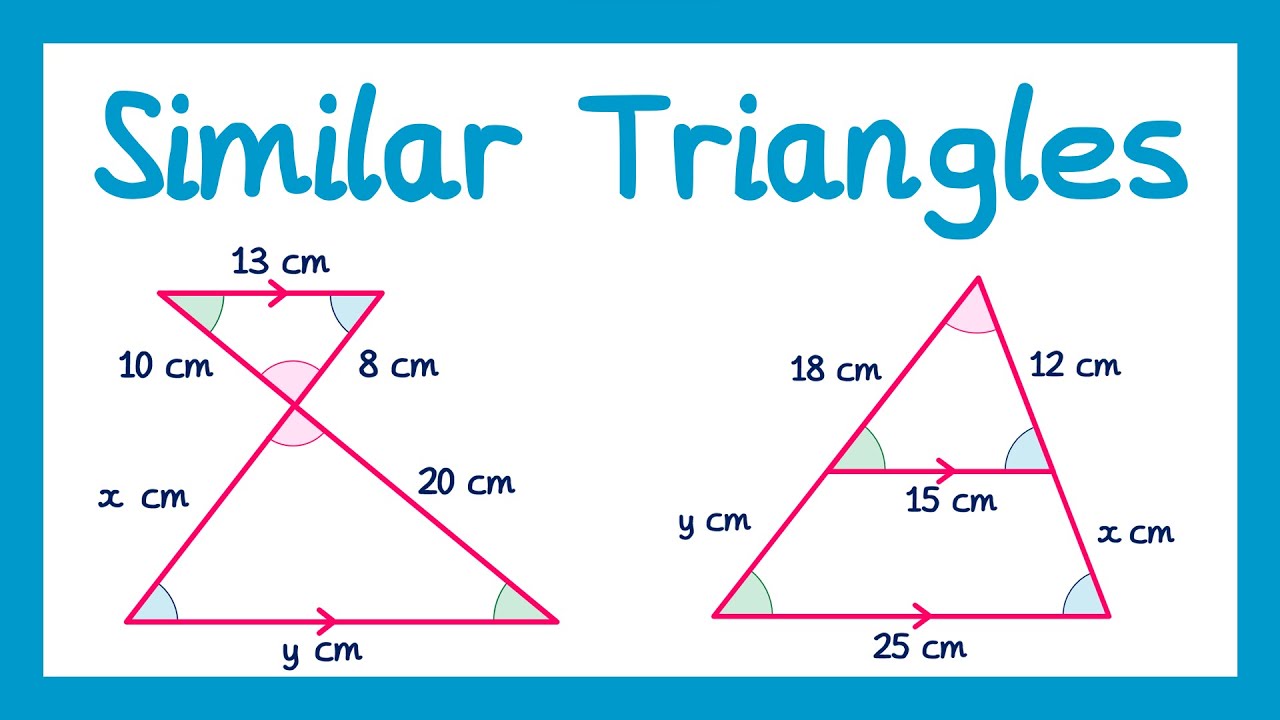
In this educational video, the lesson focuses on the concept of similar triangles, exploring key properties and problem-solving techniques. The script includes explanations about congruent angles, parallel lines, and proportional relationships between sides in similar triangles. Through several examples, such as determining the position of point E, calculating the length of DE, and applying the properties of similar triangles, students are guided through critical thinking exercises. The material, aligned with the Merdeka Curriculum for SMP students, emphasizes a hands-on approach to understanding geometry, supported by visual aids and calculations.

Takeaways

• 😀 The lesson focuses on similarity in triangles, specifically discussing the relationship between triangles ABC and ADE.
• 😀 A key concept is that similar triangles have corresponding angles equal and the lengths of corresponding sides proportional.
• 😀 The script explains how to identify similar triangles by examining matching angles and proportional side lengths.
• 😀 The importance of using the properties of congruent angles to prove triangle similarity is emphasized throughout.
• 😀 The lesson includes a step-by-step solution for determining the location of point E in a triangle based on its similarity with another triangle.
• 😀 The script demonstrates how to use the Pythagorean theorem to find unknown sides of a triangle, such as calculating the length of AC.
• 😀 The calculation of triangle areas is discussed, including the formula for the area of a triangle using its base and height.
• 😀 There is a focus on using ratios to find unknown side lengths in similar triangles, such as using the ratio of AD to AB to determine the length of DE.
• 😀 Several examples are worked through to show how the properties of similar triangles can be applied to solve real-world problems.
• 😀 The lesson includes practice problems with solutions to help reinforce the concepts of triangle similarity, congruence, and area calculations.

Q & A

What is the concept being taught in this lesson?

The lesson focuses on similar triangles and how to apply the properties of similar triangles to solve problems. It includes exercises on proving triangle similarity and using proportionality for calculations.

What does it mean for two triangles to be similar?

Two triangles are considered similar if their corresponding angles are equal, and the lengths of their corresponding sides are proportional.

Why is triangle ABC similar to triangle ADE in this lesson?

Triangle ABC is similar to triangle ADE because they share equal corresponding angles, as explained by the fact that angle A is equal to angle A (due to being vertical angles) and angle B is equal to angle D (because of the property of opposite angles).

What is the significance of the parallel line BC in this problem?

The line BC is parallel to the line DE, which helps in establishing the similarity between the two triangles by ensuring the proportionality of corresponding sides.

How is the point E determined in this problem?

The point E is determined by drawing a line parallel to BC, which intersects the line AC at point E, creating the smaller, similar triangle ADE.

How is the length of segment DE calculated in this problem?

The length of segment DE is calculated using the proportion of the corresponding sides of the similar triangles. The formula used is: DE / BC = AD / AB, where values are substituted to find the length of DE.

What does the property of the sum of angles in a triangle tell us?

The sum of the interior angles of any triangle is always 180 degrees. This property is used to confirm the similarity of the triangles by ensuring that the sum of the corresponding angles in both triangles is equal.

What is the relationship between the sides of similar triangles in this lesson?

In similar triangles, the lengths of corresponding sides are proportional. This relationship is used to find missing side lengths by setting up proportions and solving for unknowns.

How is the congruence of triangle ABC with triangle ADE established?

The congruence of triangle ABC with triangle ADE is established by showing that the corresponding angles are equal and the sides are proportional, as indicated by the use of parallel lines and the properties of similar triangles.

How do we calculate the area of triangle ABC?

The area of triangle ABC is calculated using the formula for the area of a triangle: 1/2 × base × height. In this case, the base is BC and the height is the perpendicular distance from A to BC, which gives an area of 6 square cm.