Projectile Motion Lecture Part 2

Summary

This video covers the concepts of horizontal range and maximum height in projectile motion. It explains the key formulas for calculating these quantities, including the horizontal range (R) and maximum height (H), which are only applicable when launching and landing heights are the same. Through examples, the presenter demonstrates how to apply these formulas, including solving problems involving projectile motion at various angles. Additionally, it explores cases where the projectile doesn't follow the ideal conditions, such as different landing and launching heights, requiring a different approach using the motion equations. The session is designed to enhance understanding of projectile motion and its real-life applications.

Takeaways

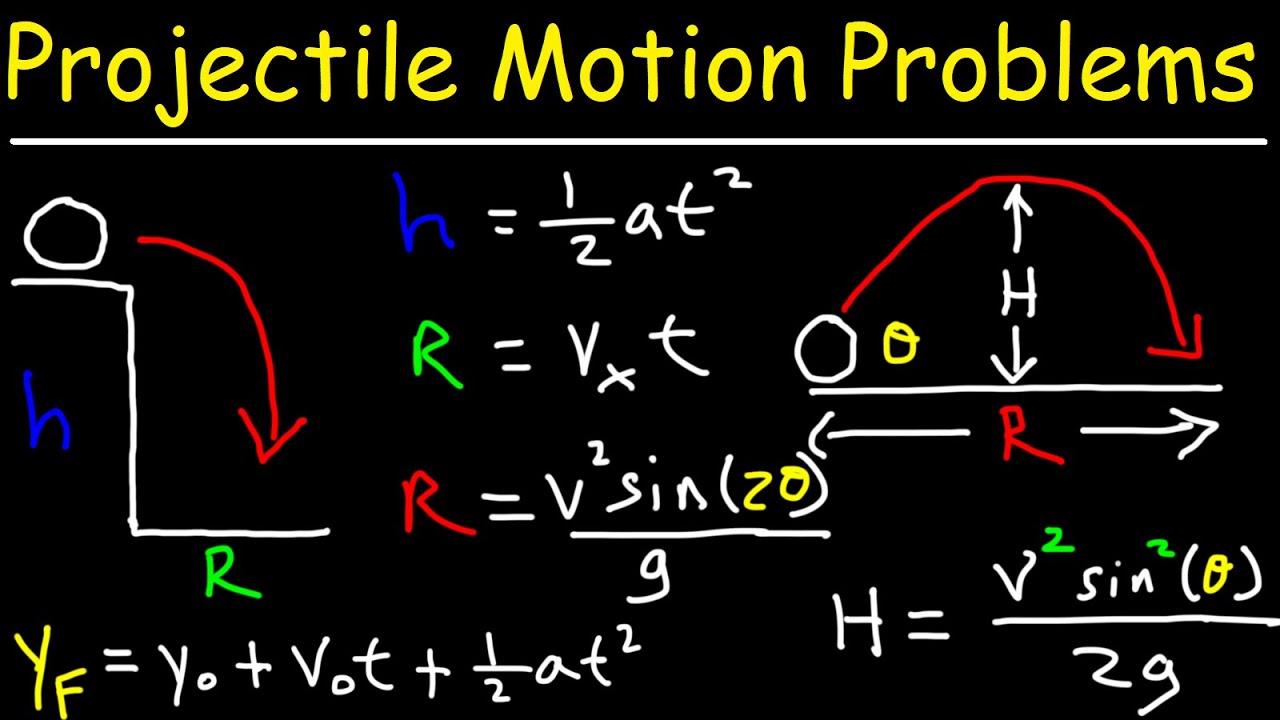
• 😀 The horizontal range of a projectile is the maximum horizontal distance it travels, and can be calculated using the formula: R = (V₀² * sin(2θ)) / g.
• 😀 The maximum height of a projectile is calculated with the formula: H = (V₀² * sin²(θ)) / 2g.
• 😀 These formulas for horizontal range and maximum height are only applicable when the launching and landing heights are equal.
• 😀 The horizontal range is maximized at an angle of 45 degrees because sine 90 degrees equals 1, making the range as large as possible.
• 😀 At angles other than 45 degrees, the range is smaller since the sine of those angles is less than 1.
• 😀 An example problem demonstrated calculating the horizontal range and maximum height of a long jump, resulting in a range of 7.94 meters and a maximum height of 0.72 meters.
• 😀 In another example, a ball is tossed from a window 8 meters above the ground at a speed of 10 m/s and an angle of 20 degrees below the horizontal.
• 😀 When launching and landing heights are not equal, the horizontal range formula cannot be used, and alternative equations must be applied to solve for time and distance.
• 😀 To solve projectile motion problems with unequal launching and landing heights, you must use a combination of equations like X = V₀ * cos(θ) * t and Y = V₀ * sin(θ) * t - 1/2 * g * t².
• 😀 The quadratic formula is often used to find the time of flight in projectile motion problems, ensuring realistic, non-negative values for time.

Q & A

What is the formula for the horizontal range of a projectile?

The formula for the horizontal range (R) of a projectile is: R = (V₀² * sin(2θ)) / g, where V₀ is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity.

Under what condition can the formulas for horizontal range and maximum height be used?

The formulas for horizontal range and maximum height can only be used when the launching height and the landing height of the projectile are equal.

At what launch angle is the horizontal range of a projectile maximized?

The horizontal range of a projectile is maximized when the launch angle is 45 degrees.

What happens to the horizontal range when the launch angle is less than or greater than 45 degrees?

When the launch angle is less than or greater than 45 degrees, the horizontal range decreases because the value of sin(2θ) becomes less than 1.

What is the formula to calculate the maximum height (H) of a projectile?

The formula to calculate the maximum height (H) of a projectile is: H = (V₀² * sin²(θ)) / (2g), where V₀ is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity.

In the example of the long jumper, what is the horizontal range of the jump?

In the example of the long jumper, the horizontal range is 7.94 meters when the jumper launches at a speed of 11 m/s and an angle of 20 degrees above the horizontal.

How is the maximum height of the long jumper calculated in the example?

The maximum height of the long jumper is calculated using the formula H = (V₀² * sin²(θ)) / (2g), where V₀ is 11 m/s, θ is 20 degrees, and g is 9.81 m/s², resulting in a maximum height of 0.72 meters.

In the second example, why can't we use the horizontal range formula to calculate the distance the ball travels?

We can't use the horizontal range formula because the launching height (from the building) and the landing height (the ground) are not the same.

What method is used to calculate the time of flight for the ball thrown from the building?

To calculate the time of flight for the ball, we use the kinematic equation for vertical motion, Y = V₀ * sin(θ) * t - (1/2) * g * t², and solve for t using the quadratic formula.

What is the time of flight for the ball tossed from the building with an initial speed of 10 m/s at a 20-degree angle below the horizontal?

The time of flight for the ball is 0.98 seconds, which is derived from solving the quadratic equation for the vertical motion of the projectile.