Projectile Motion: 3 methods to answer ALL questions!

Summary

This video tutorial explains the fundamentals of projectile motion through various examples, focusing on three main question types commonly found in exams. It covers the breakdown of vertical and horizontal components of velocity, the calculation of maximum height, time of flight, and range. Emphasizing key concepts like acceleration due to gravity and the importance of direction in calculations, the tutorial also demonstrates how to use formulas for both upward and downward projectile motion. With practical exercises and clear explanations, viewers can learn how to solve projectile motion problems efficiently.

Takeaways

• 😀 Projectile motion involves the combination of horizontal and vertical motions, with gravity affecting only the vertical component.
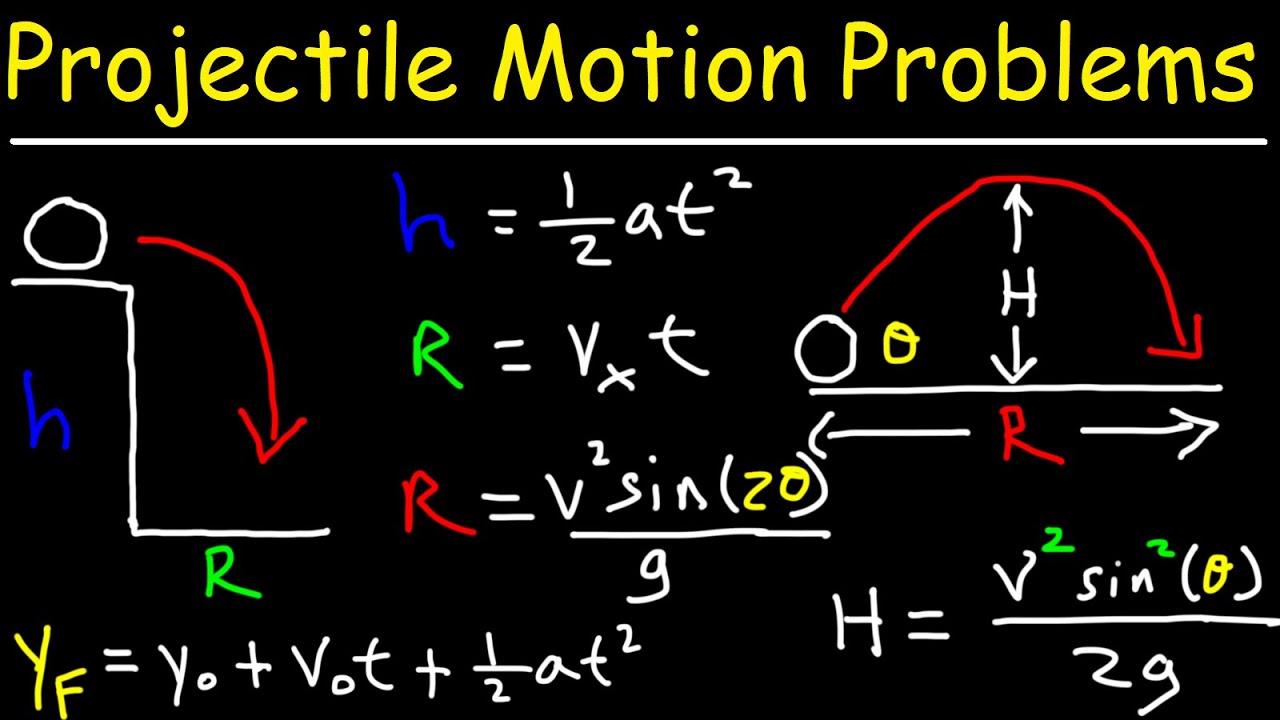
• 😀 There are three main types of projectile motion problems: where the projectile starts and ends at the same height, where it's thrown straight, and the more complex ones where the starting and ending heights differ.
• 😀 Horizontal velocity remains constant throughout projectile motion as gravity does not influence horizontal movement.
• 😀 Vertical velocity, however, is influenced by gravity, causing it to decrease as the projectile rises and increase as it falls.
• 😀 When analyzing projectile motion, it is crucial to separate vertical and horizontal components of motion to solve the problems correctly.
• 😀 The velocity of a projectile at any given point can be broken into vertical and horizontal components using trigonometric functions like sine and cosine.
• 😀 The vertical and horizontal components of velocity are calculated differently: vertical uses sine for angles less than 90°, and horizontal uses cosine.
• 😀 When solving for maximum height or range, always use vertical components for vertical calculations and horizontal components for horizontal calculations.
• 😀 For problems where a projectile is launched from a height, use kinematic equations like v² = u² + 2as to find vertical displacement or velocity.
• 😀 Time of flight can be calculated using vertical velocity and the acceleration due to gravity, keeping in mind that time is the same for both vertical and horizontal components in projectile motion.

Q & A

What are the three main types of projectile motion questions covered in the video?

The three main types of projectile motion questions are: 1) The projectile starts and ends at the same height, 2) The projectile is thrown straight, and 3) The projectile starts from a different height and ends at a different height.

What is the basic concept of projectile motion explained in the video?

Projectile motion refers to the curved path a projectile follows when it is thrown, which includes both vertical and horizontal components. The ball's vertical velocity decreases as it rises, increases as it falls, while its horizontal velocity remains constant.

How do you break down velocity into horizontal and vertical components?

Velocity can be divided into horizontal and vertical components based on the angle of launch. The vertical component is calculated using the sine function (v_vertical = v * sin(θ)), and the horizontal component is calculated using the cosine function (v_horizontal = v * cos(θ)).

What is the significance of gravity in projectile motion?

Gravity affects the vertical motion of the projectile by causing it to accelerate downward. However, gravity does not impact the horizontal velocity, so the horizontal motion remains constant throughout the flight.

How do you determine the maximum height of a projectile?

To find the maximum height, you can use the formula v² = u² + 2as, where v is the final vertical velocity (zero at maximum height), u is the initial vertical velocity, a is the acceleration due to gravity, and s is the height. The formula helps solve for the height reached by the projectile.

What formula do you use to find the time of flight in projectile motion?

The time of flight can be found using the vertical motion equations, typically using the formula v = u + at, where v is the final vertical velocity, u is the initial vertical velocity, a is acceleration due to gravity, and t is time.

Why is horizontal velocity unaffected by gravity?

Horizontal velocity is unaffected by gravity because gravity only influences the vertical direction of the motion. Since there is no acceleration in the horizontal direction, the horizontal velocity remains constant throughout the projectile's flight.

What happens when a projectile is thrown at an angle of 53° at a speed of 37 m/s?

When a projectile is thrown at a 53° angle with a speed of 37 m/s, the velocity components are divided into horizontal and vertical components. The horizontal velocity is 37 * cos(53°), and the vertical velocity is 37 * sin(53°). This helps in calculating the time of flight and the distance traveled.

How do you calculate the total range (horizontal distance) of a projectile?

The total range can be calculated by first determining the time of flight using the vertical motion equations and then using the horizontal velocity (which remains constant) to calculate the horizontal distance traveled: Range = horizontal velocity * time.

What is the importance of maintaining directional signs when solving projectile motion problems?

It is important to maintain directional signs (positive or negative) when solving projectile motion problems to correctly represent the motion in each direction. Vertical components are often treated with opposite signs for upward and downward motion to account for gravity's influence.