CONSTRUCCION DE TRIANGULOS SEGUN LA MEDIDA DE SUS LADOS Super facil - Para principiantes
Summary
TLDREn este video, Daniel Carrión explica cómo construir triángulos a partir de segmentos de recta, usando el teorema de la desigualdad triangular. Muestra cómo la suma de los dos lados más pequeños debe ser mayor que el lado más grande para que se pueda formar un triángulo. A través de varios ejemplos, demuestra los casos en los que sí y no se pueden formar triángulos, ilustrando cómo verificar si las condiciones se cumplen. Al final, invita a los espectadores a resolver ejercicios y participar en los comentarios, mientras los anima a darle like, compartir y suscribirse.
Takeaways
- 😀 La suma de los dos lados más pequeños de un triángulo debe ser mayor que el lado más grande para que se pueda formar un triángulo.
- 😀 Si la condición de la suma no se cumple, no se puede formar un triángulo.
- 😀 Ejemplo: Con segmentos de 3 cm, 4 cm y 10 cm no se puede formar un triángulo porque 3 + 4 = 7, que no es mayor que 10.
- 😀 Ejemplo: Con segmentos de 7 cm, 11 cm y 6 cm sí se puede formar un triángulo porque 7 + 6 = 13, que es mayor que 11.
- 😀 Al realizar ejercicios, se debe comprobar siempre la suma de los dos lados más pequeños con respecto al lado más grande.
- 😀 Si la suma de los dos lados más pequeños es igual al lado más grande, no se puede formar un triángulo (como en el inciso b: 6 cm + 6 cm = 12 cm).
- 😀 Un triángulo equilátero tiene tres lados iguales, como en el inciso e con 3 cm, 3 cm y 3 cm.
- 😀 En el inciso h, si la suma de los dos lados más pequeños es mayor que el lado más largo, como 6 cm + 12 cm = 18 cm > 15 cm, se puede formar un triángulo.
- 😀 Si la suma de los dos lados más pequeños es menor que el lado más largo, como en el inciso f (5 cm + 3 cm = 8 cm < 11 cm), no se puede formar un triángulo.
- 😀 Ejercicio práctico: En los incisos a, c, d, e, y y j, se aplica la misma regla de la suma de los lados más pequeños para determinar si es posible formar un triángulo.
Q & A
¿Cuál es la condición principal para poder construir un triángulo?
-La condición principal es que la suma de los dos lados más pequeños debe ser mayor que el lado más grande.
¿Qué sucede si la suma de los dos lados más pequeños no es mayor que el lado más grande?
-Si la suma de los dos lados más pequeños no es mayor que el lado más grande, no se puede construir un triángulo.
En el primer ejercicio con los segmentos de 3 cm, 4 cm y 10 cm, ¿se puede formar un triángulo?
-No, porque la suma de los lados más pequeños (3 cm + 4 cm = 7 cm) no es mayor que el lado más grande (10 cm), por lo tanto no se puede formar un triángulo.
¿Qué ocurre cuando los tres segmentos no se juntan al intentar formar un triángulo?
-Cuando los segmentos no se juntan, significa que no cumplen con la condición de la suma de los lados más pequeños siendo mayor que el lado más grande, por lo que no se puede formar un triángulo.
En el segundo ejercicio con los segmentos de 7 cm, 11 cm y 6 cm, ¿se puede formar un triángulo?
-Sí, porque la suma de los dos lados más pequeños (7 cm + 6 cm = 13 cm) es mayor que el lado más grande (11 cm), por lo tanto sí se puede formar un triángulo.
¿Qué tipo de triángulo se puede formar si las tres medidas de los lados son iguales?
-Cuando las tres medidas de los lados son iguales, se forma un triángulo equilátero.
En el inciso b con los lados de 6 cm, 6 cm y 12 cm, ¿se puede formar un triángulo?
-No, porque la suma de los dos lados más pequeños (6 cm + 6 cm = 12 cm) es igual al lado más largo, por lo que no se puede formar un triángulo.
En el inciso f con los segmentos de 11 cm, 5 cm y 3 cm, ¿se puede formar un triángulo?
-No, porque la suma de los dos lados más pequeños (5 cm + 3 cm = 8 cm) es menor que el lado más largo (11 cm), por lo que no se puede formar un triángulo.
En el inciso h con los lados de 6 cm, 15 cm y 12 cm, ¿se puede formar un triángulo?
-Sí, porque la suma de los dos lados más pequeños (6 cm + 12 cm = 18 cm) es mayor que el lado más largo (15 cm), por lo que sí se puede formar un triángulo.
¿Por qué en el inciso j con los segmentos de 3 cm, 2 cm y 9 cm no se puede formar un triángulo?
-No se puede formar un triángulo porque la suma de los dos lados más pequeños (3 cm + 2 cm = 5 cm) es menor que el lado más largo (9 cm).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
TEOREMA DE TALES Super facil - Para principiantes

Teorema de Napoleón

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera

PERIMETRO DE UN CUADRO CONOCIENDO LA DIAGONAL (Teorema de pitágoras)

PENDIENTE DE UNA RECTA A PARTIR DE DOS PUNTOS Super facil - Para principiantes
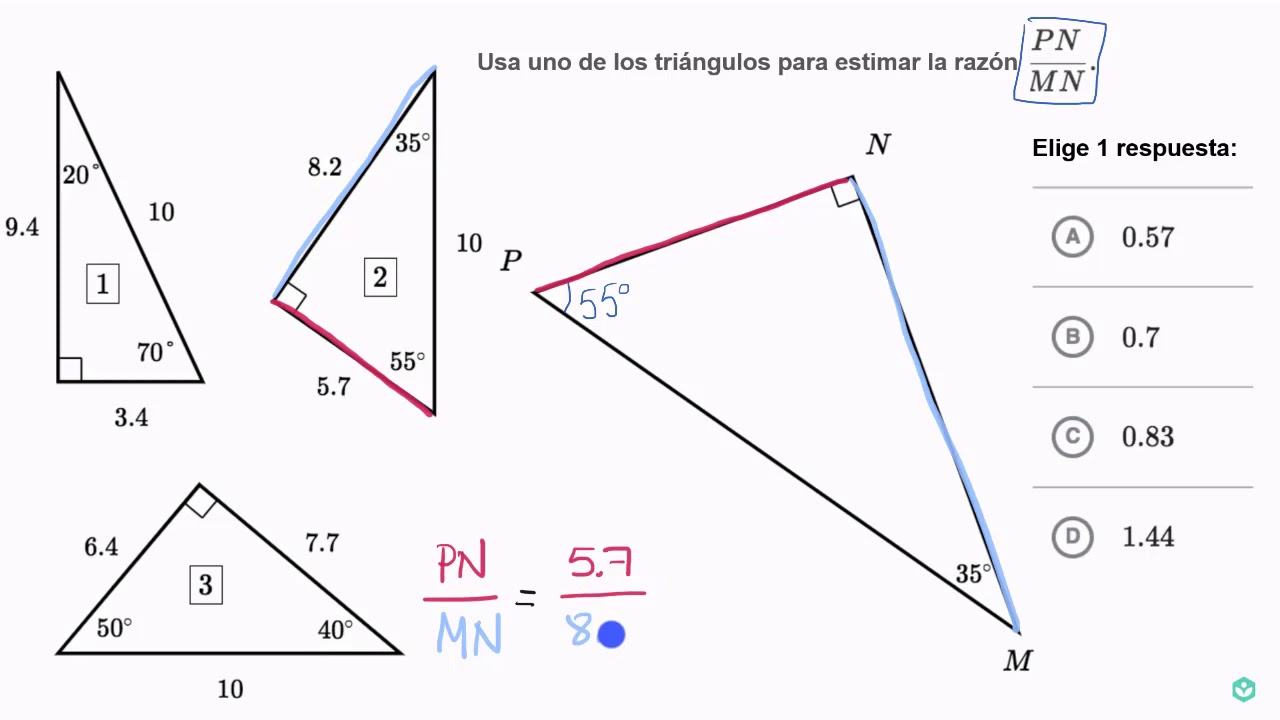
Usar semejanza para estimar la razón entre las longitudes de los lados
5.0 / 5 (0 votes)
