PERIMETRO DE UN CUADRO CONOCIENDO LA DIAGONAL (Teorema de pitágoras)
Summary
TLDREn este video, Daniel Carreón explica cómo calcular el perímetro de un cuadrado a partir de su diagonal utilizando el teorema de Pitágoras. A través de un ejemplo con una diagonal de 7 cm, muestra cómo el cuadrado se divide en dos triángulos rectángulos. Luego, utiliza la fórmula de Pitágoras para encontrar la medida de los catetos y, finalmente, calcula el perímetro del cuadrado. Además, invita a los espectadores a resolver ejercicios similares y a interactuar con el contenido, fomentando la participación mediante comentarios y suscripciones.
Takeaways
- 😀 El perímetro de un cuadrado se puede calcular utilizando el teorema de Pitágoras si conocemos la medida de su diagonal.
- 😀 Un cuadrado con una diagonal de 7 cm se divide en dos triángulos rectángulos, lo que facilita el uso del teorema de Pitágoras.
- 😀 En un triángulo rectángulo, la hipotenusa es el lado frente al ángulo de 90° y los otros dos lados son los catetos.
- 😀 Los catetos en el triángulo rectángulo, derivados de un cuadrado, tienen la misma longitud.
- 😀 El teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
- 😀 En el caso del cuadrado, la fórmula de Pitágoras se puede expresar como: c² = a² + a².
- 😀 Al sustituir valores en la ecuación, la diagonal de 7 cm permite calcular la longitud de los catetos, que es 4.949 cm.
- 😀 Conociendo la medida de los catetos, se puede calcular el perímetro del cuadrado usando la fórmula: perímetro = lado × 4.
- 😀 El perímetro del cuadrado con catetos de 4.949 cm es 19.79 cm.
- 😀 Se propone un ejercicio adicional para practicar, en el que se debe calcular el perímetro de un cuadrado con una diagonal de 10 cm.
- 😀 El video invita a los espectadores a resolver ejercicios, comentar, dar 'like' y suscribirse para más contenido educativo.
Q & A
¿Qué es el perímetro de un cuadrado?
-El perímetro de un cuadrado es la suma de las longitudes de sus cuatro lados. Se calcula multiplicando la medida de un lado por 4.
¿Cómo se calcula el perímetro de un cuadrado conociendo su diagonal?
-Para calcular el perímetro de un cuadrado conociendo su diagonal, primero se debe utilizar el teorema de Pitágoras para encontrar la longitud de los lados del cuadrado. Luego, se multiplica ese valor por 4.
¿Qué dice el teorema de Pitágoras?
-El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Qué representa la hipotenusa en un triángulo rectángulo?
-La hipotenusa es el lado opuesto al ángulo recto de un triángulo rectángulo. En este caso, es la diagonal del cuadrado.
¿Por qué los catetos del triángulo rectángulo son iguales en este ejercicio?
-Los catetos son iguales porque el triángulo rectángulo es la mitad de un cuadrado, y los dos catetos corresponden a los lados del cuadrado.
¿Qué fórmula se usa para calcular la longitud de los catetos en este caso?
-Se utiliza el teorema de Pitágoras: c² = a² + b², donde c es la hipotenusa (la diagonal del cuadrado) y a y b son los catetos, que son iguales en este caso.
¿Cómo se encuentra la longitud de los catetos cuando la diagonal es de 7 cm?
-Se sustituye la medida de la diagonal en el teorema de Pitágoras. Al resolver la ecuación, se obtiene que cada cateto mide aproximadamente 4.949 cm.
¿Qué pasa cuando se calcula el perímetro de un cuadrado con un lado de 4.949 cm?
-El perímetro se calcula multiplicando el valor del lado por 4, resultando en un perímetro de 19.79 cm.
¿Qué ocurre si la diagonal del cuadrado cambia?
-Si la diagonal cambia, la longitud de los catetos también cambiará, lo que afectará el perímetro del cuadrado. Se debe realizar el cálculo del teorema de Pitágoras nuevamente para encontrar los nuevos valores.
¿Qué significa que el cuadrado tenga una diagonal de 10 cm en el segundo ejemplo?
-Cuando se menciona un cuadrado con una diagonal de 10 cm, significa que se debe aplicar el teorema de Pitágoras para encontrar la longitud de los catetos y luego calcular el perímetro correspondiente.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Hallar el área de un Cuadrado conociendo la longitud de su Diagonal.

PERÍMETRO, ÁREA Y VOLUMEN Super Fácil - Para principiantes

PERÍMETRO Y ÁREA DEL CÍRCULO Super facil - Para principiantes.

Cálculo del área y perímetro de un Hexágono

PERÍMETRO Y ÁREA DEL ROMBO Super fácil - Para principiantes
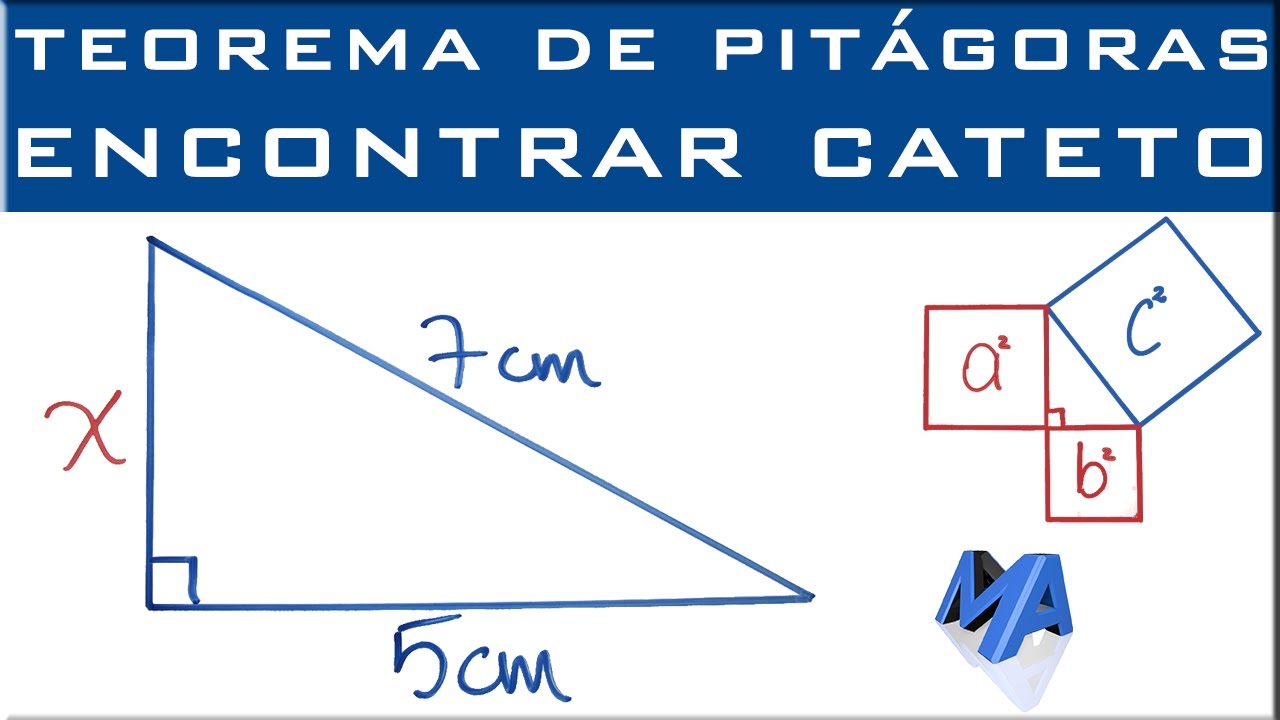
Teorema de Pitágoras | Encontrar un cateto
5.0 / 5 (0 votes)
