(Part 1) PELUANG MATEMATIKA SMA KELAS 10 #kurikulummerdeka #matematikasma #bukupaket

Summary

This educational video focuses on teaching the concept of probability, including the sample space and the likelihood of various events occurring. The instructor explains how to calculate probabilities using dice examples, discussing different types of events, such as independent and dependent events, and how to apply addition rules. Key topics include calculating the probability of specific outcomes, the meaning of certain events (e.g., rolling a pair of dice), and how to analyze the fairness of games based on probabilities. The video is designed to deepen understanding of these core mathematical concepts through interactive problem-solving.

Takeaways

• 😀 Probability refers to the likelihood of an event occurring in the future, such as the chances of rain or the likelihood of being infected by a virus.
• 😀 Probability is a measure of the chance that a certain event will or will not happen, with values ranging from 0 (impossible) to 1 (certain).
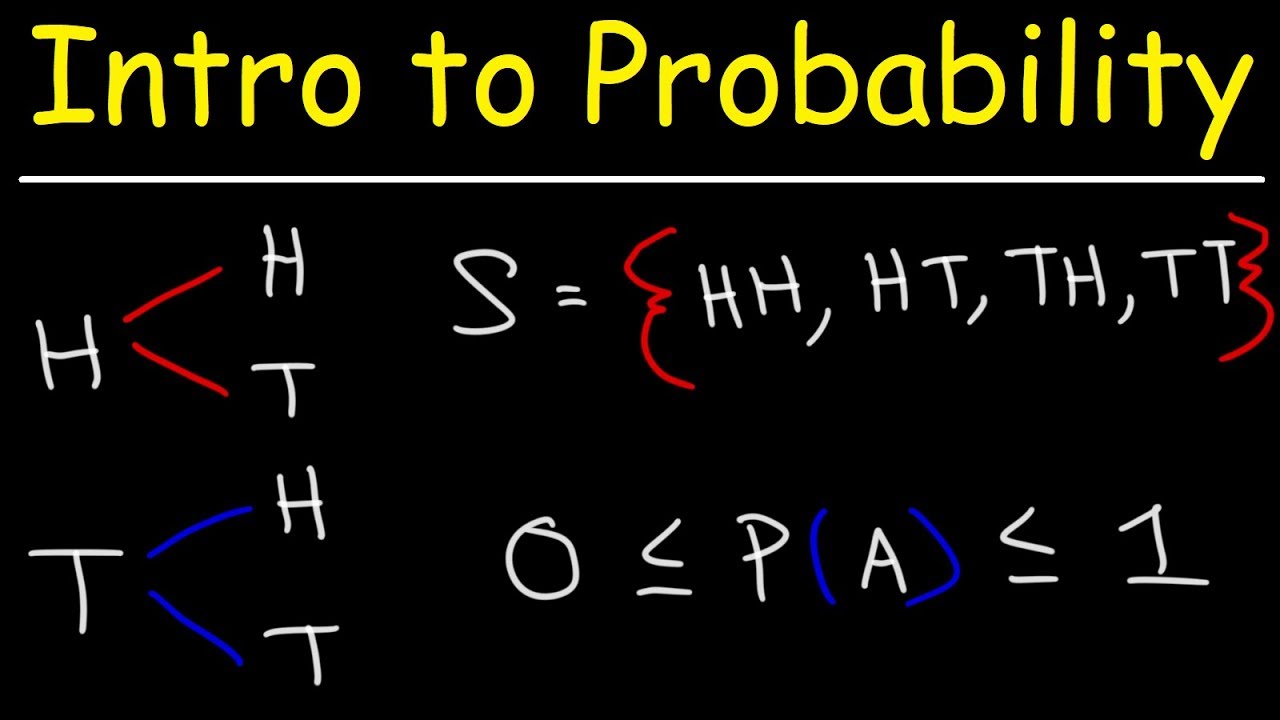
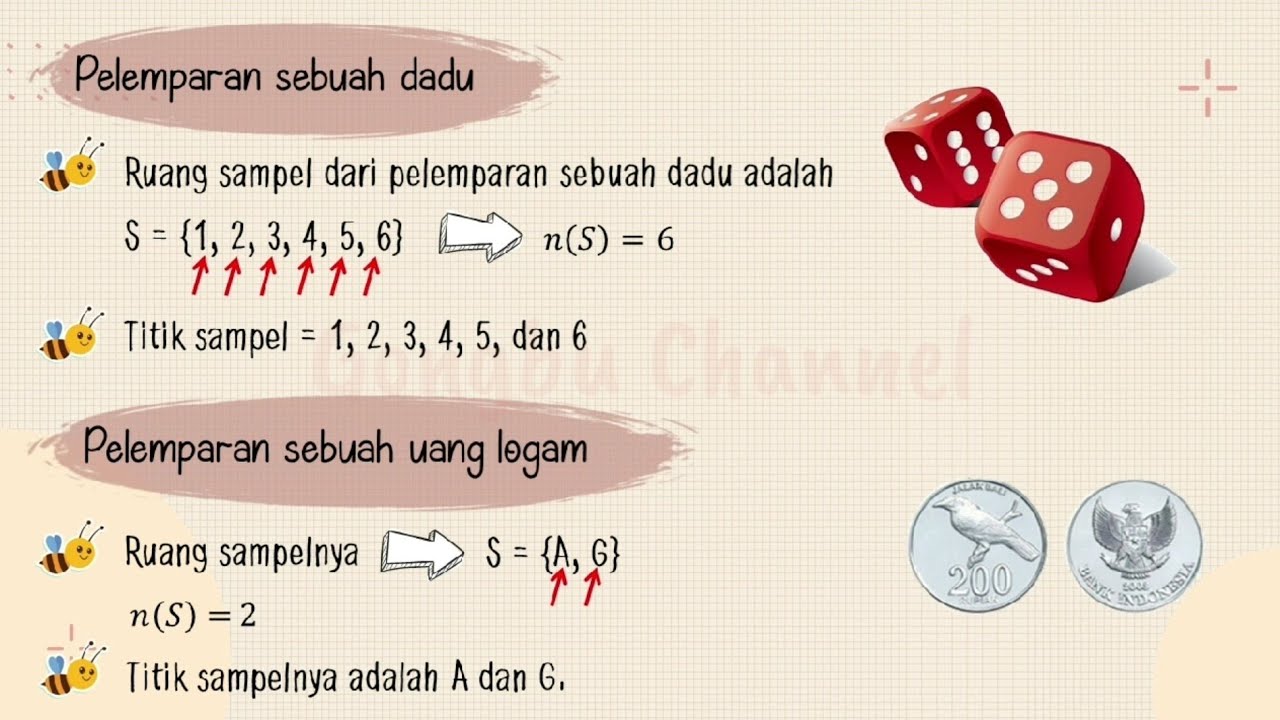
• 😀 The sample space (S) represents the set of all possible outcomes in an experiment, and each outcome is referred to as a sample point.
• 😀 When calculating probability, the formula used is P(A) = Na / Ns, where Na is the number of favorable outcomes, and Ns is the total number of possible outcomes in the sample space.
• 😀 An event can either be certain (probability = 1), impossible (probability = 0), or somewhere in between.
• 😀 In probability, the outcomes are typically considered to have an equal chance of happening if the system is fair (e.g., a fair die).
• 😀 When rolling two dice, the order of the dice matters, so 3,2 is different from 2,3 due to the distinction between the dice.
• 😀 If the dice are indistinguishable (e.g., both are the same color), the probability of outcomes like 3,2 and 2,3 becomes the same, which reduces the total number of unique outcomes.
• 😀 The probability of getting a specific result (like a sum of 11) when rolling two dice is calculated by determining how many combinations result in that sum and dividing by the total number of possible outcomes.
• 😀 When combining probabilities of different events, the addition rule is used, which helps to find the probability of either event A or event B occurring (denoted as A or B).

Q & A

What is the main topic discussed in the video?

The main topic of the video is probability, which involves understanding the likelihood or chance of events occurring in the future, such as predicting rainfall or the probability of a person contracting COVID-19.

How is probability defined in this context?

Probability is defined as a measure of the likelihood of an event happening or not happening in the future. It can be expressed as a value between 0 and 1.

What are some examples of events where probability can be applied?

Examples include predicting the likelihood of rain, the chance of a person contracting COVID-19, or the probability of a person having blood type AB.

What is the significance of sample space in probability?

Sample space refers to the set of all possible outcomes in an experiment or trial. For example, in the case of rolling two dice, the sample space includes all the possible outcomes from each die.

What does the notation NS represent in probability?

NS represents the number of elements in the sample space, which is the total number of possible outcomes in an experiment.

What is the formula for calculating the probability of an event?

The probability of an event is calculated using the formula: P(A) = Na / NS, where Na is the number of favorable outcomes, and NS is the total number of possible outcomes in the sample space.

What happens when you roll two dice that are distinguishable by color (red and white)?

When rolling two distinguishable dice, such as a red die and a white die, each combination (e.g., 3,2) is distinct from the reverse combination (2,3), resulting in a total of 36 possible outcomes.

What is the probability of rolling a pair of the same number on two dice?

The probability of rolling a pair of the same number (e.g., 1,1; 2,2) on two dice is 6/36, or 1/36 for each specific pair.

How do you calculate the probability of getting at least one die showing the number 5?

The probability of getting at least one die showing the number 5 is calculated by counting all combinations where at least one die shows a 5. The favorable outcomes are 11, which gives a probability of 11/36.

What is the difference between getting at least one 4 and getting two identical numbers on two dice?

The probability of getting at least one 4 is 11/36, while the probability of getting two identical numbers (such as 1,1 or 2,2) is 6/36. Therefore, it is more likely to get at least one 4 than two identical numbers.