Tree Diagrams - Corbettmaths
Summary
TLDRThis video explains the concept of tree diagrams in probability, demonstrating how to use them to calculate the likelihood of various outcomes. It covers how to represent multiple events and their probabilities, such as John and Dan throwing balls at a target or Chloe shooting an arrow. The video shows step-by-step how to calculate the probabilities for different outcomes using the multiplication and addition rules, including how to find the probability of multiple events occurring together or separately. It's an engaging and educational guide for understanding and applying probability concepts using tree diagrams.
Takeaways
- 😀 Tree diagrams are a useful tool for representing the possible outcomes of multiple events in probability problems.
- 😀 The basic rule for tree diagrams is to multiply probabilities along branches for sequential events.
- 😀 Each branch of a tree diagram represents a possible outcome of an event, with the probabilities on each branch summing to 1.
- 😀 The probability of a sequence of events occurring is found by multiplying the probabilities of each event along the branches.
- 😀 If multiple events are mutually exclusive (i.e., one event or another occurs), the probabilities are added together.
- 😀 When calculating the probability of multiple independent events, each event's probability is represented by a branch in the tree diagram.
- 😀 A tree diagram helps visualize all possible outcomes and their associated probabilities in a clear, systematic way.
- 😀 In the example of John and Dan throwing balls at a target, the probabilities of different outcomes are calculated based on their individual probabilities of hitting or missing the target.
- 😀 The final probabilities of combined outcomes (e.g., 'John hits and Dan misses') are found by multiplying the individual probabilities on the branches.
- 😀 In the example with Chloe firing an arrow, tree diagrams can also handle fractional probabilities, such as the probability of windy conditions or Chloe hitting the target in different weather conditions.
Q & A
What is a tree diagram in probability?
-A tree diagram is a visual representation used to show all the possible outcomes of two or more events, and it's particularly useful in solving probability problems.
How do you determine the probability of each outcome in a tree diagram?
-To determine the probability of each outcome, you multiply the probabilities along the branches. This follows the 'and' rule in probability, where the combined probability of two events is the product of their individual probabilities.
What does the sum of probabilities along each pair of branches in a tree diagram add up to?
-The sum of the probabilities along each pair of branches must always equal 1. This is because the events covered by the branches are mutually exclusive and exhaustive.
If the probability of an event happening is 0.6, what is the probability of it not happening?
-If the probability of an event happening is 0.6, the probability of it not happening would be 1 - 0.6 = 0.4.
What is the probability that John and Dan both hit the target if the probability of John hitting is 0.6 and Dan hitting is 0.7?
-The probability that both John and Dan hit the target is calculated by multiplying their individual probabilities: 0.6 * 0.7 = 0.42.
How do you calculate the probability that exactly one person hits the target?
-The probability that exactly one person hits the target is the sum of the probabilities of the two mutually exclusive outcomes: John hits and Dan misses, or John misses and Dan hits. This can be calculated as 0.18 + 0.28 = 0.46.
How do you find the probability of at least one person hitting the target?
-The probability of at least one person hitting the target is the sum of the probabilities of the outcomes where at least one person hits the target. These include 'hit-hit', 'hit-miss', and 'miss-hit'. Adding them together: 0.42 + 0.18 + 0.28 = 0.88.
In a tree diagram with events that can either happen or not happen, how do you label the branches for a new event?
-For a new event, you label the branches with the probability of each outcome. For example, if the probability of an event occurring is 1/4, the other branch (event not occurring) would be labeled with the complement, which is 3/4.
In the example with Chloe firing an arrow, how do you calculate the probability of her hitting the target on a windy day?
-To calculate the probability of Chloe hitting the target on a windy day, multiply the probability of it being windy (1/5) by the probability of her hitting the target on a windy day (1/4). This gives 1/5 * 1/4 = 1/20.
What is the total probability that Chloe hits the target, considering both windy and not windy conditions?
-To find the total probability that Chloe hits the target, add the probabilities for 'windy and hit' and 'not windy and hit'. The total probability is 1/20 (windy and hit) + 8/15 (not windy and hit), which simplifies to 35/60 or 7/12.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Mengenal Ruang Sampel, Titik Sampel dan Kejadian

Gr 11 Probability: Tree diagram

Peluang ~ Menentukan Nilai Peluang dan Frekuensi Harapan Suatu Kejadian (Materi PJJ Klas VIII/8 SMP)
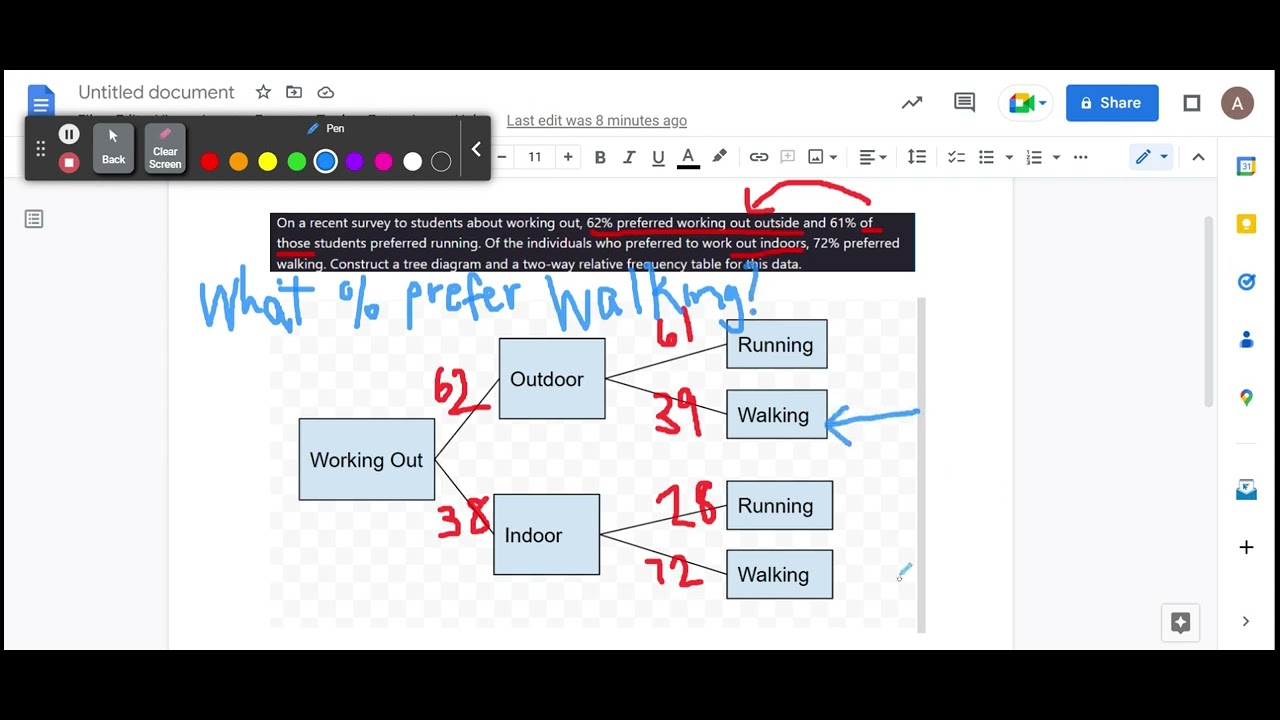
2.04 Create and analyze tree diagram
PELUANG l DASAR TEORI PELUANG

Artificial Intelligence | PROBABILITAS BERSYARAT (CONDITIONAL PROBABILITY)
5.0 / 5 (0 votes)