Ecuación de la parábola | Gráfica y ecuación conociendo vértice y foco Ejemplo 1
Summary
TLDREn este video, el instructor enseña cómo graficar una parábola y encontrar su ecuación cuando se conocen el vértice y el foco. Se explican los conceptos clave como el vértice, el foco, la directriz y el parámetro 'p', que determina la forma de la parábola. A través de ejemplos prácticos, se muestra cómo graficar la parábola paso a paso y cómo identificar hacia dónde abre. Además, se enseña a escribir la ecuación canónica de la parábola, dependiendo de la orientación, usando la fórmula adecuada. La explicación se enfoca en la comprensión visual y conceptual, evitando el memorizar fórmulas.
Takeaways
- 😀 Para graficar una parábola necesitamos tres elementos clave: el vértice, el foco y la directriz.
- 😀 El orden para trabajar con estos elementos es: foco, vértice y directriz. Es importante recordar este orden para facilitar los ejercicios.
- 😀 Una frase mnemotécnica que puede ayudar a recordar el orden es 'fui volando', que representa foco, vértice, directriz.
- 😀 Al graficar, primero ubicamos el vértice y luego el foco, y a partir de esos puntos trazamos la directriz perpendicularmente.
- 😀 La distancia entre el vértice y el foco es conocida como 'p', y esta distancia también define la posición de la directriz.
- 😀 La parábola abre dependiendo de la posición del foco y la directriz. Puede abrir hacia la derecha, izquierda, arriba o abajo.
- 😀 En el ejercicio mostrado, si la parábola abre hacia la izquierda, la ecuación será de la forma (x - h)² = -4p(y - k).
- 😀 La fórmula de la parábola cambia dependiendo de la dirección en la que se abre: hacia la derecha se utiliza x positiva, hacia arriba se usa y positiva, y hacia abajo se utiliza y negativa.
- 😀 La ecuación canónica de una parábola se forma reemplazando las coordenadas del vértice, el valor de p y la dirección en la fórmula estándar.
- 😀 Es recomendable graficar la parábola y trabajar visualmente en lugar de memorizar fórmulas complicadas, ya que esto facilita la comprensión y la resolución de ejercicios.
Q & A
¿Qué tres elementos son necesarios para graficar una parábola?
-Para graficar una parábola, necesitamos conocer tres elementos: el vértice, la distancia p (que es la distancia entre el vértice y el foco), y hacia dónde abre la parábola (hacia la derecha, izquierda, arriba o abajo).
¿Cuál es el orden en el que se deben identificar el foco, vértice y directriz?
-El orden correcto es: primero el foco, luego el vértice, y finalmente la directriz. Este orden se aplica independientemente de la dirección en que la parábola abra.
¿Qué significa que la parábola abre hacia la izquierda?
-Si la parábola abre hacia la izquierda, significa que la apertura de la parábola se extiende en la dirección de los valores negativos del eje X en el plano cartesiano.
¿Cómo se calcula la distancia p?
-La distancia p es la distancia entre el vértice y el foco, y también es la misma distancia entre el vértice y la directriz. En el ejemplo proporcionado, esta distancia es de 2 unidades.
¿Por qué es importante conocer la distancia p al graficar la parábola?
-La distancia p es crucial porque nos permite determinar el lado recto de la parábola, el cual es paralelo a la directriz y pasa por el foco. Esta información nos ayuda a trazar la parábola correctamente.
¿Qué es la ecuación canónica de una parábola que abre hacia la izquierda?
-La ecuación canónica de una parábola que abre hacia la izquierda tiene la forma: (y - k)² = -4p(x - h), donde (h, k) es el vértice, p es la distancia entre el vértice y el foco, y el signo negativo indica que la parábola abre hacia la izquierda.
¿Cómo se encuentra la ecuación de la parábola cuando se conoce el vértice, el foco y la dirección de apertura?
-Para encontrar la ecuación, se sustituyen los valores del vértice (h, k) y la distancia p en la ecuación canónica de la parábola correspondiente según su dirección de apertura. Por ejemplo, para una parábola que abre hacia la derecha, la ecuación sería (y - k)² = 4p(x - h).
¿Cuál es la importancia de la frase 'fui volando' en el proceso de graficar una parábola?
-'Fui volando' es una frase mnemotécnica que ayuda a recordar el orden correcto de los elementos: foco, vértice y directriz, lo cual facilita el proceso de graficar la parábola de manera ordenada y precisa.
¿Cómo se determina si una parábola abre hacia la derecha o hacia la izquierda?
-Si una parábola abre hacia la derecha, el eje X es positivo, y si abre hacia la izquierda, el eje X es negativo. La forma de la ecuación canónica también ayuda a determinar la dirección: si la X tiene un signo negativo en la ecuación, la parábola abre hacia la izquierda.
¿Qué se debe hacer cuando se encuentran dos negativos en la ecuación de la parábola?
-Cuando se encuentran dos negativos, estos se pueden simplificar, ya que el producto de dos negativos da un valor positivo. Es común borrar los signos negativos y colocar un signo positivo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Ex 2: Conic Section: Parabola with Vertical Axis and Vertex NOT at the Origin (Down)

Ecuación de la parábola dado vértice, foco │ fuera origen

Elementos de una parábola dada ecuación │ origen

Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)

Shifted Conics | Parabolas where the Vertex is not the Origin, Finding Focus and Directrix
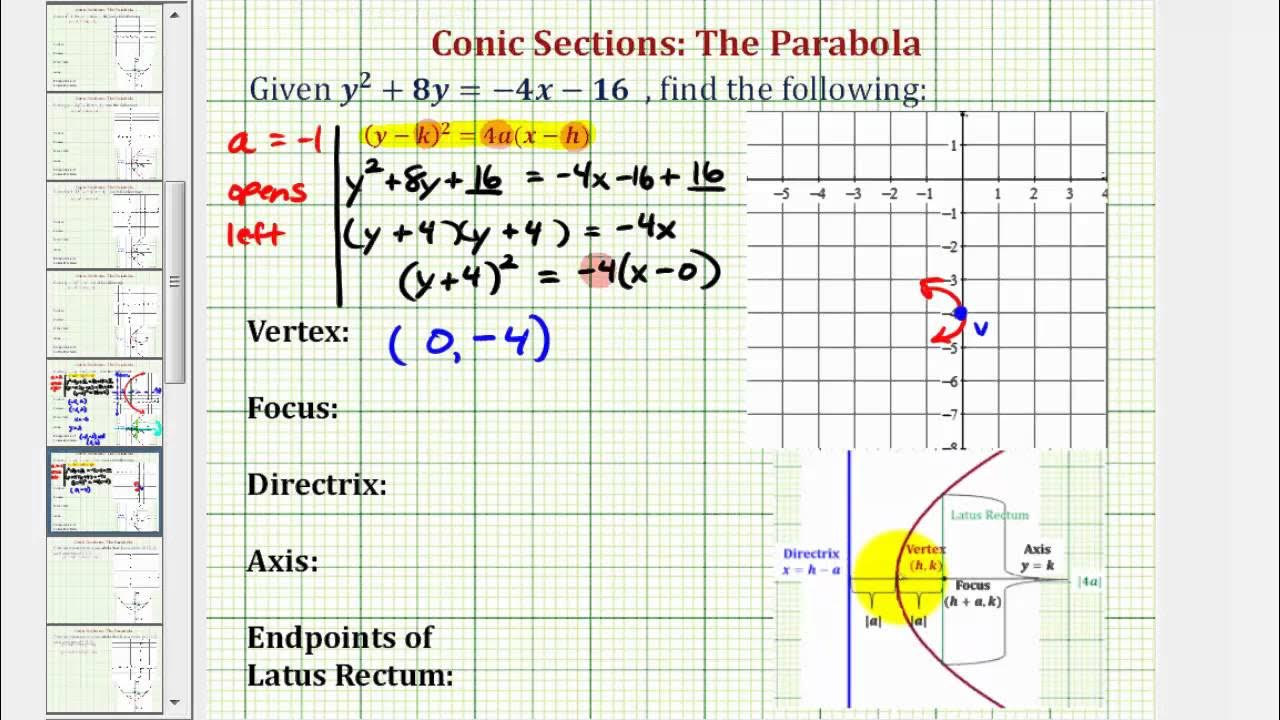
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)
5.0 / 5 (0 votes)
