Ecuación de la parábola dado vértice, foco │ fuera origen
Summary
TLDREste ejercicio enseña cómo obtener la ecuación de una parábola dado su vértice y foco. Se explica cómo identificar los elementos clave: el vértice, el valor de p (distancia entre vértice y foco), y si la parábola es horizontal o vertical. A través de gráficos, se muestra cómo calcular el lado recto y cómo simplificar la ecuación ordinaria a la forma general. Además, se detallan ejemplos prácticos con diferentes vértices, focos y directrices, destacando la importancia de sustituir los valores de h, k y p en las ecuaciones para obtener las formas correctas. También se cubre cómo desarrollar y ordenar la ecuación general.
Takeaways
- 😀 El primer paso para obtener la ecuación de una parábola es conocer el vértice.
- 😀 El valor de 'p' es crucial, ya que representa la distancia entre el vértice y el foco.
- 😀 Para determinar la orientación de la parábola (horizontal o vertical), hay que observar la posición del foco con respecto al vértice.
- 😀 Si el foco está a la izquierda o derecha del vértice, la parábola será horizontal.
- 😀 Si el foco está por encima o debajo del vértice, la parábola será vertical.
- 😀 La fórmula general para la ecuación de una parábola horizontal es: (y - k)^2 = 4p(x - h).
- 😀 La fórmula general para la ecuación de una parábola vertical es: (x - h)^2 = 4p(y - k).
- 😀 El valor de 'p' puede ser positivo o negativo dependiendo de la dirección en la que la parábola se abre (hacia la derecha/arriba o izquierda/abajo).
- 😀 El lado recto de la parábola se calcula como 4 veces el valor absoluto de 'p', y determina cuán abierta está la parábola.
- 😀 Si se requiere la ecuación general, se debe desarrollar la ecuación ordinaria expandiendo los binomios y igualándola a cero.
- 😀 En la ecuación general de una parábola, el término cuadrático de 'x' o 'y' aparece primero, seguido del término lineal y los números constantes.
Q & A
¿Qué se necesita para obtener la ecuación de una parábola?
-Para obtener la ecuación de una parábola, se necesita conocer tres elementos clave: el vértice, el valor de p (distancia entre el vértice y el foco) y saber si la parábola es horizontal o vertical.
¿Cómo se determina si una parábola es horizontal o vertical?
-La orientación de la parábola (horizontal o vertical) se determina observando la posición del foco en relación al vértice. Si el foco se mueve horizontalmente con respecto al vértice, la parábola es horizontal. Si se mueve verticalmente, la parábola es vertical.
¿Qué es el valor de p en la ecuación de una parábola?
-El valor de p es la distancia entre el vértice y el foco. Esta distancia puede ser positiva o negativa dependiendo de si el foco está a la derecha (positivo) o a la izquierda (negativo) para una parábola horizontal, o hacia arriba (positivo) o hacia abajo (negativo) para una parábola vertical.
¿Cómo se calcula el lado recto de una parábola?
-El lado recto de una parábola se calcula multiplicando el valor absoluto de p por 4. Esto determina la distancia total a lo largo de la parábola desde el foco, dividiéndola simétricamente por encima y por debajo del eje de la parábola.
¿Cuál es la fórmula de la ecuación ordinaria de una parábola horizontal?
-La fórmula de la ecuación ordinaria de una parábola horizontal es: (y - k)² = 4p(x - h), donde (h, k) son las coordenadas del vértice y p es la distancia desde el vértice al foco.
¿Qué significa desarrollar la ecuación ordinaria de una parábola?
-Desarrollar la ecuación ordinaria de una parábola implica expandir los binomios al cuadrado, simplificar los términos y luego igualar la ecuación a cero para obtener la forma general de la ecuación.
¿Qué es una ecuación general de una parábola?
-Una ecuación general de una parábola es una forma algebraica que no tiene términos cuadrados aislados y está en la forma estándar de una cónica, que incluye los términos de x², x, y y un número constante igualado a cero.
¿Cómo se calcula el valor de p cuando se conoce la directriz de una parábola?
-Cuando se conoce la directriz de una parábola, el valor de p se calcula como la distancia entre el vértice y el foco. Si el foco se encuentra en la misma dirección que la directriz, la distancia se mide entre el vértice y el foco, que se encuentra del lado opuesto a la directriz.
¿Qué sucede si se tiene una parábola con foco y vértice sobre un eje horizontal?
-Si una parábola tiene el foco y el vértice sobre un eje horizontal, la parábola será horizontal y su ecuación tendrá la forma (y - k)² = 4p(x - h), donde h y k son las coordenadas del vértice y p es la distancia desde el vértice al foco.
¿Cómo se organiza la ecuación general de una parábola en su forma estándar?
-La ecuación general de una parábola en su forma estándar debe organizarse primero con el término de x², luego el término de x, seguido por el término de y y finalmente los números constantes, con todos los términos igualados a cero.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Ecuación de la parábola | Gráfica y ecuación conociendo vértice y foco Ejemplo 1

Ex 2: Conic Section: Parabola with Vertical Axis and Vertex NOT at the Origin (Down)

Exercise 1 Parabola

Elementos de una parábola dada ecuación │ origen

🧲 PARÁBOLA: Concepto y elementos (foco, vértice, L.R, directriz, distancia focal) | Juliana la profe
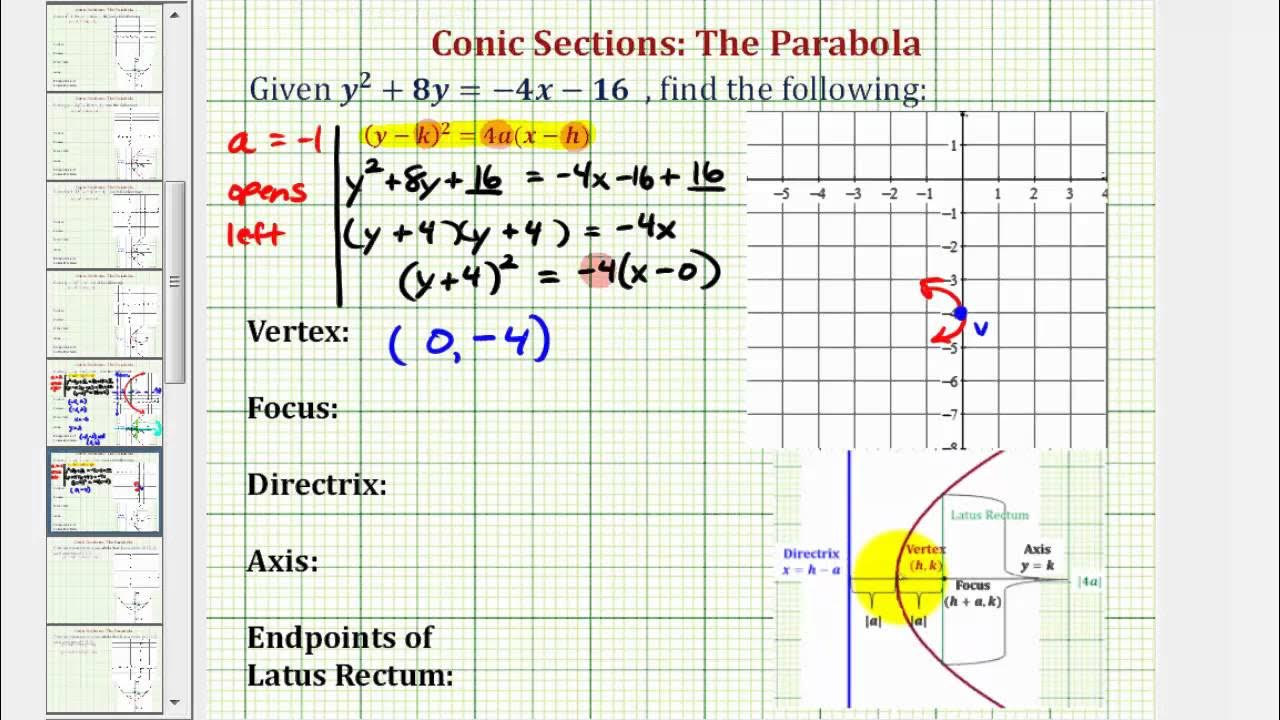
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)
5.0 / 5 (0 votes)
