FUNCIÓN CUADRÁTICA - Cómo graficarla calculando todos sus puntos mas importante
Summary
TLDREste video tutorial enseña cómo graficar una función cuadrática paso a paso, comenzando con el cálculo y la ubicación de puntos clave como el vértice, las raíces, la ordenada al origen y el eje de simetría. Se explica cómo usar las fórmulas para encontrar el vértice y las raíces, cómo identificar la intersección con el eje y y cómo trazar la parábola de manera precisa en una hoja cuadriculada. Es un recurso útil para quienes desean entender el proceso de graficado de funciones cuadráticas de forma clara y detallada.
Takeaways
- 😀 El vértice es uno de los puntos más importantes de la parábola, ya que es donde se originan las dos ramitas.
- 😀 La fórmula para calcular la coordenada x del vértice es: x = -b / (2a).
- 😀 La coordenada y del vértice se encuentra sustituyendo el valor de x en la ecuación original de la parábola.
- 😀 El coeficiente 'a' es el número que acompaña a la x², 'b' es el coeficiente de la x, y 'c' es el término independiente.
- 😀 Las raíces de la parábola se encuentran usando la fórmula cuadrática: x = (-b ± √(b² - 4ac)) / 2a.
- 😀 Si el discriminante (b² - 4ac) es negativo, la ecuación no tiene raíces reales.
- 😀 La ordenada es el valor de la parábola cuando x = 0, y es igual al término independiente 'c'.
- 😀 El eje de simetría de la parábola es una línea vertical que pasa por el vértice y tiene la ecuación x = coordenada x del vértice.
- 😀 Para graficar la parábola, es útil usar papel cuadriculado para obtener una representación precisa y ordenada.
- 😀 Al graficar, se debe asegurarse de que la parábola sea simétrica respecto al eje de simetría, y reflejar los puntos de un lado al otro para lograr una curva equilibrada.
Q & A
¿Cuál es la fórmula para calcular la coordenada x del vértice de una parábola?
-La fórmula para calcular la coordenada x del vértice es: x = -b / (2a), donde 'a' es el coeficiente de x² y 'b' es el coeficiente de x en la ecuación cuadrática.
¿Cómo se calcula la coordenada y del vértice de una parábola?
-Para calcular la coordenada y del vértice, se sustituye el valor de x obtenido en la fórmula del vértice en la ecuación cuadrática original.
¿Qué pasos debo seguir para encontrar las raíces de una parábola?
-Para encontrar las raíces, utilizamos la fórmula cuadrática: x = (-b ± √(b² - 4ac)) / 2a. Primero sustituimos los valores de a, b y c, y luego resolvemos para encontrar las dos posibles raíces.
¿Qué pasa si el discriminante (b² - 4ac) es negativo al calcular las raíces?
-Si el discriminante es negativo, significa que no existen raíces reales, ya que no se puede calcular la raíz cuadrada de un número negativo.
¿Qué es la ordenada o intersección con el eje y?
-La ordenada es el punto donde la parábola corta al eje y. Para encontrarla, se establece x = 0 en la ecuación cuadrática y se resuelve para y.
¿Por qué es importante la simetría de la parábola al graficarla?
-La simetría de la parábola es fundamental porque nos permite usar un lado de la parábola para reflejar y completar el otro lado, garantizando una gráfica precisa.
¿Qué es el eje de simetría de la parábola?
-El eje de simetría es una línea vertical que pasa por el vértice de la parábola, dividiéndola en dos partes iguales. Su ecuación es x = (valor de la coordenada x del vértice).
¿Cómo se determina la posición del vértice en el gráfico?
-El vértice se ubica en las coordenadas (x, y), donde x se calcula usando la fórmula x = -b / (2a) y y se obtiene sustituyendo x en la ecuación cuadrática original.
¿Qué ocurre si el término independiente (c) es negativo al encontrar la ordenada?
-Si el término independiente c es negativo, el valor de la ordenada será negativo, lo que significa que la parábola corta el eje y por debajo del origen.
¿Cómo puedo mejorar la precisión al graficar una parábola en papel cuadriculado?
-Para mejorar la precisión, se recomienda utilizar papel cuadriculado, marcar el eje cartesiano con precisión y usar los puntos calculados (vértice, raíces y ordenada) para trazar la parábola, aprovechando la simetría.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Funciones Cuadráticas (Definición, propiedades y representación)

Función cuadrática dada en forma factorizada

FUNCIÓN CUADRÁTICA: Explicación Completa y Cómo Graficarla

Función cuadrática. Gráfico: hallando vértice, raíces, ordenada al origen. Parte1/7
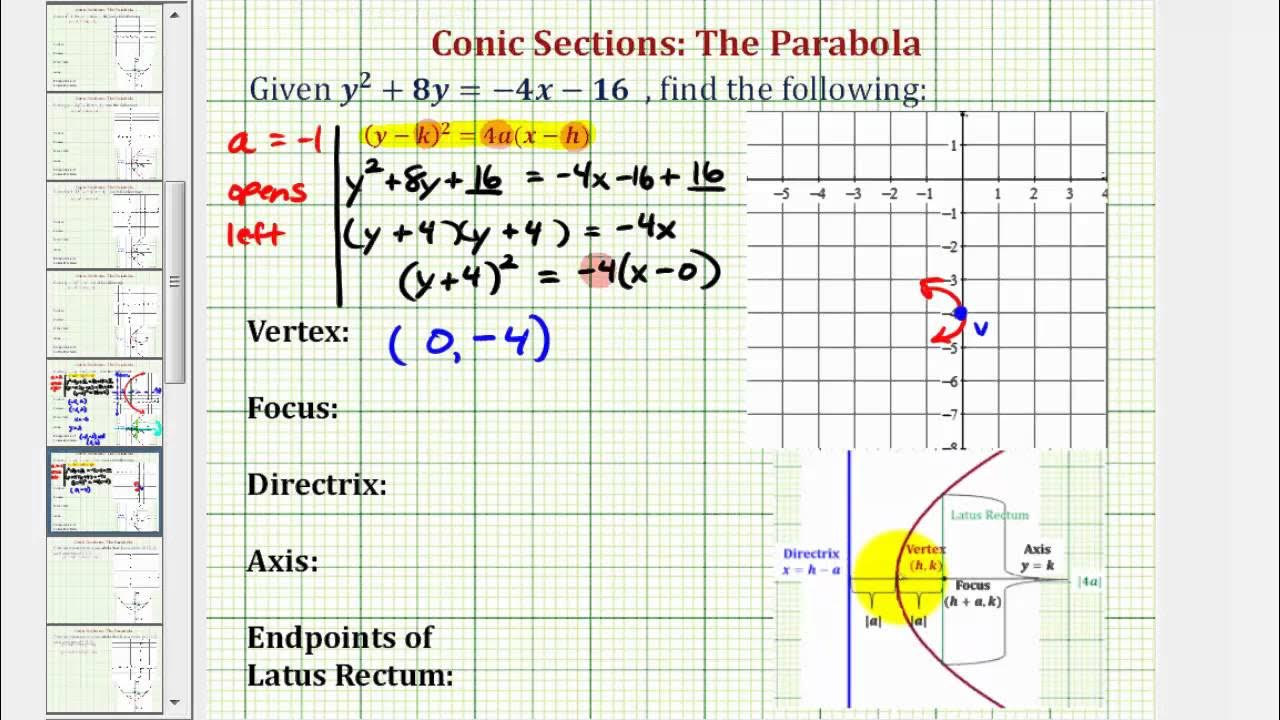
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)

Funciones CUADRÁTICAS 📝 Vértice, Puntos de Corte con los ejes y Representación
5.0 / 5 (0 votes)
