Menyusun fungsi kuadrat (part 1)

Summary

This tutorial teaches how to solve quadratic functions using three methods: when the x-intercepts are given, when the vertex coordinates are known, and when three arbitrary points are provided. The first method uses the formula y = a(x - p)(x - q) when the x-intercepts (p, 0) and (q, 0) are known. The second method, for vertex coordinates, uses y = a(x - h)^2 + k. The third method, for arbitrary points, uses y = ax² + bx + c. Through a worked example, the steps for finding the equation of a parabola are clearly demonstrated, from finding the value of 'a' to calculating the final quadratic equation.

Takeaways

• 😀 The script covers the process of constructing quadratic functions, focusing on three methods depending on the information given in the problem.
• 😀 The first method involves using the x-intercepts (p, 0) and (q, 0) to find the quadratic equation.
• 😀 The second method is used when the coordinates of the vertex (the turning point) of the parabola are known.
• 😀 The third method is for when three arbitrary points on the parabola are provided.
• 😀 When using the x-intercepts, the formula y = a(x - p)(x - q) is applied.
• 😀 When using the vertex, the formula y - k = a(x - h)^2 is used, where (h, k) is the vertex.
• 😀 When three points are given, the general quadratic formula y = ax² + bx + c is applied.
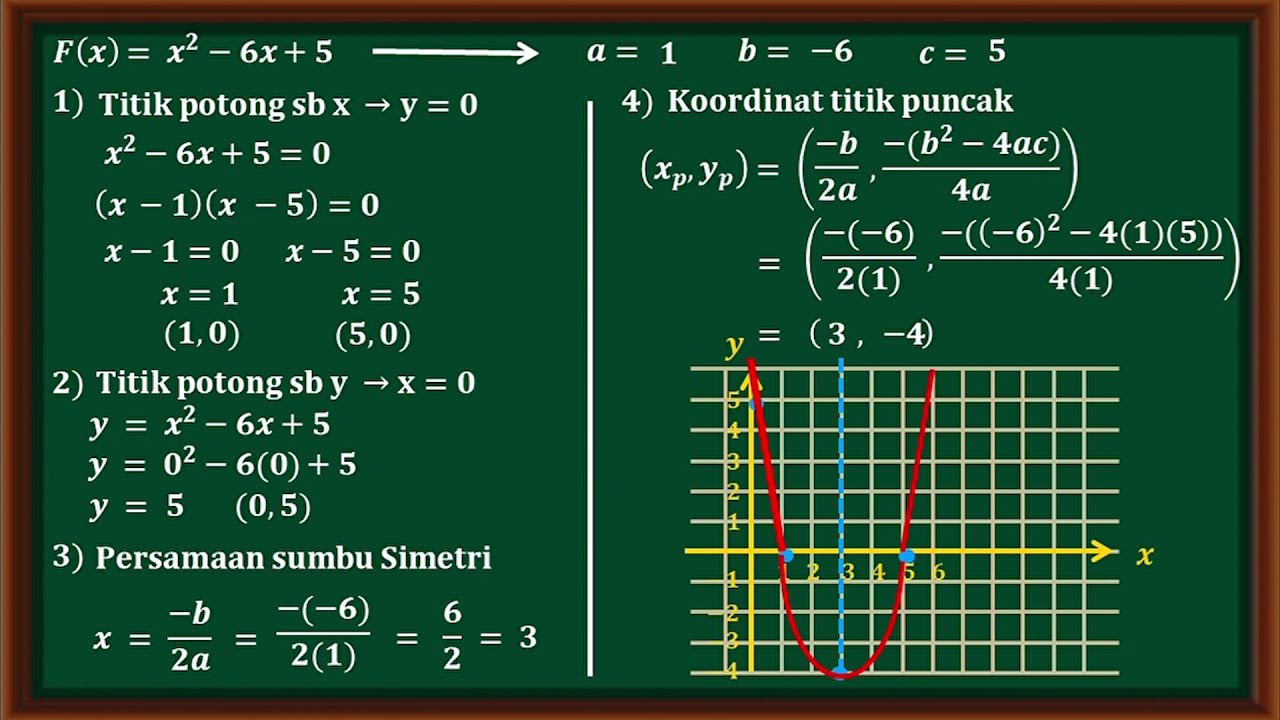
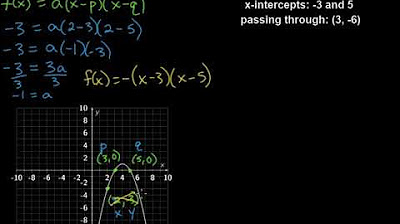
• 😀 In the example given, the parabola cuts the x-axis at (-1/2, 0) and (-3, 0), so the first formula is used.
• 😀 To find the value of 'a' in the equation, substitute the known values of x, y, p, and q into the formula and solve.
• 😀 After determining the value of 'a', the full quadratic equation can be written by substituting all the known values.

Q & A

What are the three methods for solving quadratic functions based on the script?

The three methods for solving quadratic functions are: 1) Using the x-intercepts (the points where the curve intersects the x-axis), 2) Using the vertex coordinates (the turning point or peak of the parabola), and 3) Using three arbitrary points on the parabola.

How do we use the x-intercepts to find the equation of a parabola?

If the x-intercepts are given as points (p, 0) and (q, 0), the equation of the parabola can be written as y = a(x - p)(x - q), where 'a' is a constant that needs to be determined.

What formula is used when the coordinates of the vertex (turning point) are given?

When the vertex coordinates (h, k) are known, the formula used is y - k = a(x - h)^2. The value of 'a' can be found by substituting a known point on the parabola into the equation.

What formula is used when three arbitrary points on the parabola are known?

When three arbitrary points are given, the general quadratic equation y = ax^2 + bx + c is used, and the constants a, b, and c are determined by substituting the points into the equation and solving the system of equations.

In the example given, how are the values of p and q identified?

In the example, the parabola intersects the x-axis at the points (-1/2, 0) and (-3, 0), so p = -1/2 and q = -3.

How is the value of 'a' determined in the example problem?

The value of 'a' is found by substituting the known point (-1, 2) into the equation y = a(x - p)(x - q) and solving for 'a'. After calculations, it is determined that a = -2.

What is the final equation of the parabola in the example problem?

The final equation of the parabola in the example is y = -2x^2 - 7x - 3.

What role do the points (-1/2, 0) and (-3, 0) play in solving the equation?

The points (-1/2, 0) and (-3, 0) are the x-intercepts, which allow the use of the formula y = a(x - p)(x - q) to set up the equation of the parabola.

Why is it necessary to substitute the point (-1, 2) into the equation when solving for 'a'?

Substituting the point (-1, 2) into the equation y = a(x - p)(x - q) allows us to solve for the unknown value 'a', which is essential to determine the exact equation of the parabola.

What does the variable 'a' represent in the quadratic equation?

The variable 'a' represents the coefficient that affects the direction and width of the parabola. It determines whether the parabola opens upwards or downwards and how wide or narrow it appears.