Menyusun Rumus Fungsi Kuadrat #fazanugas

Summary

This video tutorial explains how to determine the quadratic function formula from a graph by covering three conditions. First, it discusses finding the formula when the graph intersects the X-axis at two points. Then, it demonstrates how to derive the formula using the vertex and another point. Lastly, it explores how to calculate the quadratic equation when the graph passes through three arbitrary points. Step-by-step examples are provided to guide viewers through identifying key points, substituting into the quadratic formula, and solving for constants to form the equation.

Takeaways

• 😀 Understanding how to determine the quadratic function formula from the graph is the primary goal of the video.
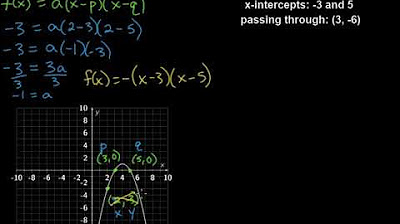
• 😀 The first case involves graphs that intersect the x-axis at two points. You can use the formula y = a(x - x1)(x - x2) to find the quadratic function.
• 😀 To find the value of 'a' in the first case, substitute the known points into the equation and solve for 'a'.
• 😀 The second case involves graphs that pass through the vertex and one other point. The vertex form of the quadratic equation is used: y = a(x - xp)^2 + yp.
• 😀 In the second case, you calculate 'a' by substituting the known vertex and point into the equation.
• 😀 The third case involves arbitrary points. For this, use the general quadratic equation y = ax^2 + bx + c and substitute the points to form a system of linear equations.
• 😀 A system of three equations is formed by substituting three points into the general quadratic equation.
• 😀 Solving the system of linear equations helps to determine the values of 'a', 'b', and 'c' for the quadratic equation.
• 😀 The third case shows how to use elimination and substitution methods to solve the system of equations and find the quadratic function.
• 😀 The video concludes by offering a practice problem for the viewers to apply the learned methods and find the quadratic function for a given graph.

Q & A

What is the general form of a quadratic function used in this tutorial?

The general form of a quadratic function used in this tutorial is y = ax^2 + bx + c.

In the first scenario, how do you identify the x-intercepts from a graph?

The x-intercepts are the points where the graph crosses the x-axis. In the example, these are the points (1,0) and (4,0).

What is the formula to find the quadratic function when given the x-intercepts?

The formula used is y = a(x - x1)(x - x2), where x1 and x2 are the x-intercepts of the graph.

How do you determine the value of 'a' in the equation when using the x-intercepts?

You substitute a known point on the graph into the equation and solve for 'a'. For example, using the point (0,2), you substitute into y = a(x - 1)(x - 4), and solve for 'a'.

How do you expand the equation after determining the value of 'a'?

After finding 'a', you substitute it back into the equation and expand it. For example, y = 1/2(x - 1)(x - 4) becomes y = 1/2(x^2 - 5x + 4), which simplifies to y = 1/2x^2 - 5/2x + 2.

What does the second scenario involve in terms of finding a quadratic function?

In the second scenario, the graph passes through the vertex and another point. The formula used is y = a(x - xp)^2 + yp, where (xp, yp) is the vertex of the parabola.

How do you find 'a' when using the vertex and a point on the graph?

Substitute the coordinates of the vertex and the known point into the equation y = a(x - xp)^2 + yp, then solve for 'a'. For example, using the vertex (2,3) and the point (0,-1), you substitute to find 'a'.

What is the method to solve for 'a' using the point (0, -1) in the second scenario?

Substitute (0, -1) into the equation y = a(x - 2)^2 + 3. This gives the equation -1 = a(0 - 2)^2 + 3. Simplifying, we find a = -1/4.

What is the third scenario about, and how do you solve for the quadratic function?

The third scenario involves a graph passing through three arbitrary points. You create a system of equations by substituting the coordinates of the points into the general quadratic form y = ax^2 + bx + c.

How do you solve for 'a', 'b', and 'c' using the three points in the third scenario?

You substitute the coordinates of the three points into the general equation y = ax^2 + bx + c to create a system of three equations. Then, use methods like substitution or elimination to solve the system for 'a', 'b', and 'c'.