FUNGSI INVERS KELAS 11, KONSEP DAN CONTOH SOAL mudah dipahami
Summary
TLDRThis video explains the concept of inverse functions for 11th-grade students. It introduces the basic principles of how functions link two sets, with examples to illustrate how to find the inverse of a function. The tutorial covers the process of reversing the relationship between input and output and provides step-by-step guidance to solve for the inverse. The video concludes with practice problems, encouraging students to test their understanding before the next lesson, which will focus on rational functions and more complex inverse scenarios.
Takeaways
- 😀 A function connects elements from a domain to a codomain, mapping input to output.
- 😀 The inverse function, denoted as f⁻¹, reverses the mapping of a function: input and output are swapped.
- 😀 To find f⁻¹(x), first assume f⁻¹(x) = y and use the original function to relate y to x.
- 😀 Solving for y involves algebraic manipulation, including adding, subtracting, multiplying, dividing, or using powers and roots as needed.
- 😀 For linear functions like f(x) = 2x - 3, the inverse is found by solving 2y - 3 = x, yielding f⁻¹(x) = (x + 3)/2.
- 😀 For functions involving roots, such as f(x) = √(x³ - 4) + 5, eliminate the root by raising both sides to the appropriate power, then solve for y.
- 😀 For exponential functions like f(x) = 2^x + 5, use logarithms to isolate the variable when solving for the inverse.
- 😀 The core concept is that a function and its inverse always swap input and output values.
- 😀 Step-by-step processing through the original function ensures accurate determination of the inverse.
- 😀 Practicing different types of functions, including linear, root, and rational/exponential, strengthens understanding of inverse functions.
Q & A
What is the concept of an inverse function?
-An inverse function reverses the roles of input and output. If the original function transforms an input 'a' into an output 'b', the inverse function transforms the output 'b' back to the input 'a'. The notation for the inverse function of 'F' is denoted as 'F^-1'.
How do you find the inverse of a function?
-To find the inverse of a function, you typically start by swapping the input and output. Then, solve for the original input in terms of the output. This involves manipulating the equation and performing operations like addition, subtraction, multiplication, or division to isolate the variable.
Why do we add 3 to both sides in the first example?
-We add 3 to both sides in order to move the constant term to the other side of the equation. This is part of the process of solving for 'y', which represents the inverse function in the example.
What is the significance of squaring both sides of the equation in the example with the square root?
-Squaring both sides of the equation is necessary to eliminate the square root. Since a square root is the same as raising something to the power of 1/2, squaring both sides effectively cancels out the square root, making it easier to solve for the variable 'y'.
How do you handle fractional exponents when solving for the inverse?
-Fractional exponents can be handled by raising both sides of the equation to the reciprocal of the exponent. For example, if you have a term with an exponent of 1/3, you can raise both sides of the equation to the power of 3 to eliminate the fractional exponent.
What does the notation F^-1(x) represent?
-The notation F^-1(x) represents the inverse of the function F evaluated at 'x'. It tells you the input value of the original function F that corresponds to the output 'x'.
How do you simplify a function involving a square root and cube roots?
-To simplify functions involving square roots or cube roots, use the appropriate exponent rules. For square roots, raise both sides of the equation to the power of 2, and for cube roots, raise both sides to the power of 3. This helps eliminate the root, allowing you to solve for the variable.
What happens when you apply the inverse function to a value?
-When you apply the inverse function to a value, you reverse the transformation made by the original function. For example, if the original function transforms input 'a' into output 'b', applying the inverse function to 'b' will return you to 'a'.
What is the purpose of the example with 'F^-1(5)'?
-The purpose of the example with 'F^-1(5)' is to show how to apply the inverse function to a specific value. By solving for 'a' in the equation, we find that the inverse of the function at 5 is 3.
What is meant by the term 'domain' and 'codomain' in the context of functions?
-The domain of a function refers to the set of all possible input values, while the codomain refers to the set of possible output values. The function connects each element from the domain to an element in the codomain.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
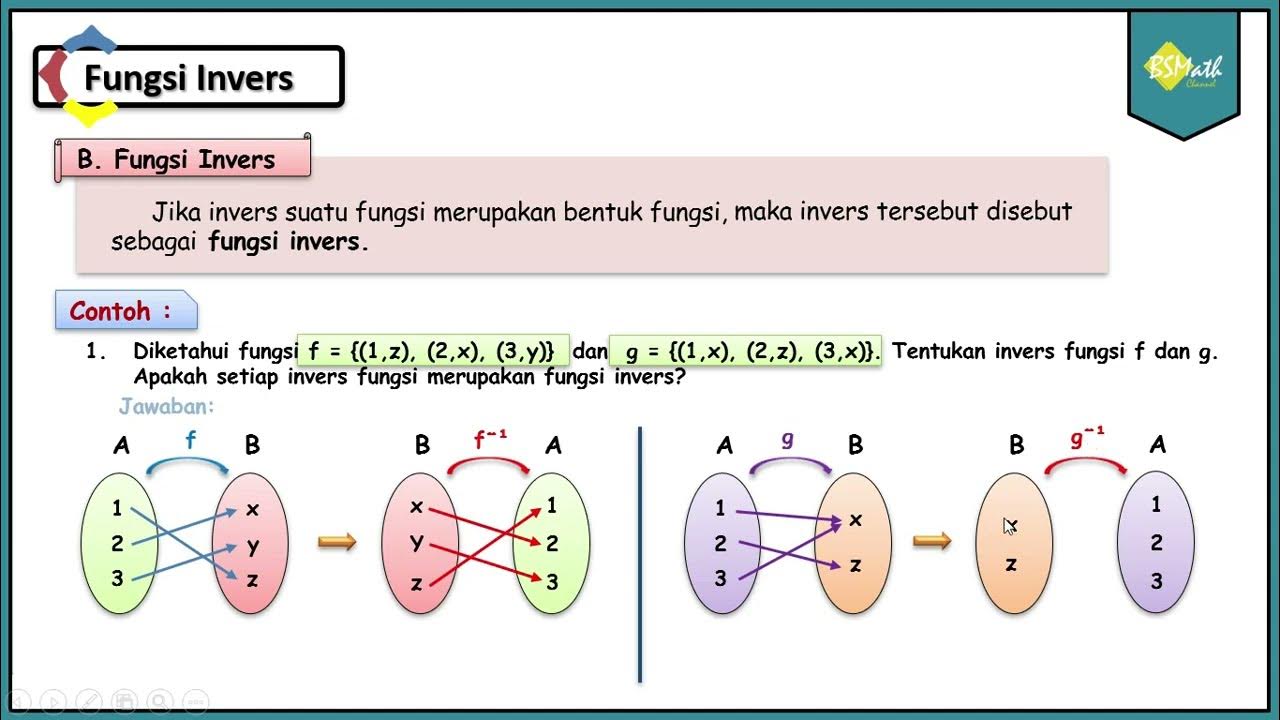
Fungsi Invers - Matematika SMA Kelas XI Kurikulum Merdeka
Fungsi Transenden 2 (Invers Fungsi dan Turunannya)
(Part 1) FUNGSI KOMPOSISI DAN FUNGSI INVERS MATEMATIKA SMA KELAS 11 #kurikulummerdeka #matematikasma

Tanda Fungsi Trigonometri Tiap Kuadran | Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka

Komposisi Fungsi - Matematika Wajib Kelas XI Kurikulum Merdeka

Rangka Aksial dan Rangka Apendikular - Sistem Rangka - Biologi Kelas XI
5.0 / 5 (0 votes)