Funciones Trigonométricas en el círculo unitario con Geogebra
Summary
TLDREn este video, el ingeniero Omar López enseña cómo construir funciones trigonométricas en el círculo unitario utilizando GeoGebra. A lo largo de 19 pasos detallados, los espectadores aprenden a crear una circunferencia de radio 1, calcular los valores de seno, coseno y tangente, y representar gráficamente estas funciones en el plano cartesiano. También se exploran los recíprocos de estas funciones, como la cosecante, secante y cotangente. El video es una guía práctica y visual para entender cómo interactúan las funciones trigonométricas en el círculo unitario y su aplicación en GeoGebra.
Takeaways
- 😀 Abre Geogebra clásico en línea y utiliza la herramienta de circunferencia para crear un círculo unitario con radio 1.
- 😀 Usa un deslizador para manipular el ángulo y vincúlalo con el ángulo en el círculo unitario mediante el símbolo Alfa.
- 😀 Inserta una perpendicular desde el punto B al eje de las X para ayudar a crear los triángulos trigonométricos.
- 😀 Crea una intersección entre la perpendicular y el eje X para formar un nuevo punto C, lo cual es esencial para los cálculos trigonométricos.
- 😀 Construye un polígono utilizando los puntos A, B y C para visualizar el triángulo formado en el círculo unitario.
- 😀 Personaliza los segmentos con colores, grosor de líneas y nombres para diferenciar el cateto opuesto, el cateto adyacente y la hipotenusa.
- 😀 Inserta y visualiza las fórmulas trigonométricas de seno, coseno y tangente, y sus recíprocos como cosecante, secante y cotangente.
- 😀 Asegúrate de que las fórmulas trigonométricas estén bien definidas en Geogebra utilizando el formato adecuado en latex.
- 😀 Verifica los valores de seno y coseno con una calculadora externa, comparándolos con los obtenidos en Geogebra para comprobar la exactitud.
- 😀 Inserta los valores de las funciones trigonométricas (seno, coseno, tangente, etc.) como texto en el gráfico, lo cual permitirá visualizar los resultados al mover el deslizador.
Q & A
¿Cuál es el propósito principal de la práctica en GeoGebra descrita en el video?
-El propósito principal es enseñar cómo representar las funciones trigonométricas en el círculo unitario utilizando GeoGebra, lo que permite visualizar y comprender mejor estas funciones en el plano cartesiano.
¿Qué herramienta de GeoGebra se utiliza para crear la circunferencia en el paso 1?
-En el paso 1, se utiliza la herramienta 'Circunferencia: Centro y Radio' para crear la circunferencia con radio 1, que representa el círculo unitario.
¿Por qué se utiliza un deslizador en el proceso de la práctica?
-El deslizador se utiliza para controlar el valor del ángulo en el círculo unitario, lo que permite visualizar cómo cambian las funciones trigonométricas (como seno, coseno y tangente) a medida que varía el ángulo.
¿Qué se debe hacer si no aparece la relación entre el ángulo y el deslizador?
-Si no aparece la relación entre el ángulo y el deslizador, es necesario asegurarse de que ambos tengan el mismo nombre, en este caso, 'Alfa', para que se vinculen correctamente.
¿Cómo se insertan las fórmulas trigonométricas en GeoGebra?
-Las fórmulas trigonométricas se insertan utilizando la herramienta de texto, donde se puede escribir en formato LaTeX las expresiones de seno, coseno, tangente y sus recíprocos, como cosecante, secante y cotangente.
¿Qué función tiene el polígono creado en el paso 7?
-El polígono creado en el paso 7 conecta los puntos A, B y C, representando un triángulo rectángulo en el círculo unitario, y es utilizado para visualizar los catetos y la hipotenusa.
¿Qué acciones se realizan en los pasos 10 y 11?
-En el paso 10 se asignan los nombres y colores correspondientes a los segmentos del triángulo, como 'cateto opuesto', 'cateto adyacente' e 'hipotenusa'. En el paso 11, se verifican los valores de seno y coseno para ángulos específicos, como 60 grados, y se comparan con los resultados de una calculadora.
¿Cómo se inserta una recta tangente en el paso 12?
-Para insertar una recta tangente, se utiliza la herramienta 'Tangente', donde se selecciona el punto de tangencia y la circunferencia, generando así una recta tangente al círculo unitario.
¿Qué modificaciones se hacen a los segmentos en el paso 16?
-En el paso 16 se cambian los colores de los segmentos que forman el triángulo, lo que facilita la visualización de los diferentes elementos trigonométricos, como el cateto opuesto, adyacente y la hipotenusa.
¿Cómo se verifica la precisión de las funciones trigonométricas creadas en GeoGebra?
-La precisión se verifica al comprobar que los valores obtenidos para las funciones trigonométricas en GeoGebra coincidan con los valores calculados usando una calculadora, lo que garantiza que las funciones sean correctas para ángulos dados.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Identidades Trigonométricas | Identidad Pitagórica | Identidades de Cofunciones |

Funciones Trigonométricas - Características Generales

Círculo trigonométrico (PRIMERA PARTE)

Construcción de líneas trigonométricas en Geogebra 2023

Entendiendo Seno y Coseno
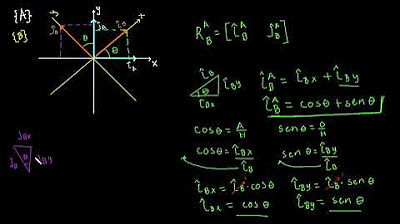
Matriz de rotación en 2d y sistemas de coordenadas
5.0 / 5 (0 votes)
