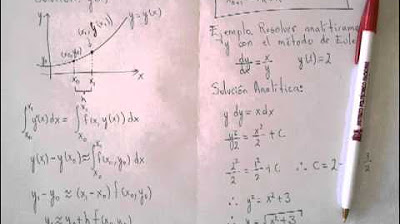Ejemplo del Método de Euler

Alfa Teorema

14 Nov 201208:19

Summary

TLDREn este script se presenta el método de Euler para resolver el problema de valor inicial de Jane de la ecuación diferencial 'dx/dt = 12x + 1' con la condición inicial 'x(0) = 4'. Se proporciona la solución analítica 'x = log(2x + 1)' y se verifica evaluando en 't=0'. Se muestra cómo calcular iterativamente usando el método de Euler, avanzando en pasos de 'h' y evaluando la función en cada paso. Se comparan los valores aproximados obtenidos para diferentes valores de 'h' con el valor exacto, destacando cómo disminuir 'h' reduce el error relativo. Se incluye una gráfica que contrasta la solución analítica con las aproximaciones numéricas para 'h = 0.5' y 'h = 0.25', mostrando que un paso más pequeño mejora la precisión del método.

Takeaways

📚 Se presenta un ejemplo de cómo resolver un problema de valor inicial utilizando el método de Euler (método de oler).
🔍 El problema específico trata de encontrar la solución de la ecuación diferencial \( \frac{dx}{dt} = 12x + 1 \) con la condición inicial \( x(0) = 4 \).
🧐 La solución analítica para este problema es \( x = \ln(2x) \), la cual se verifica evaluando en la condición inicial.
📉 La derivada de la solución analítica se obtiene y se utiliza para comparar con el método numérico.
📈 Se grafica la solución analítica en azul y se muestra cómo se aproxima con el método de Euler.
🔢 Se utiliza un valor inicial \( x_0 = 4 \) y se avanza en pasos de tamaño \( h \), evaluando la función en cada paso.
📊 Se muestran los pasos numéricos para calcular \( x_1, x_2, x_3 \) y se comparan con la solución analítica.
📉 Se crea una tabla comparando los valores exactos y los aproximados obtenidos con el método de Euler para diferentes tamaños de paso \( h \).
📉 Los errores relativos se calculan y se muestran para evaluar la precisión del método de Euler en función del tamaño de paso.
🔍 Se observa que al disminuir el tamaño de paso \( h \), la aproximación numérica mejora, aunque aumenta el número de pasos necesarios.
📈 Se incluye una gráfica que ilustra cómo las aproximaciones numéricas se acercan a la solución analítica a medida que se reducen los pasos.

Q & A

¿Qué método se utiliza para resolver el problema de valor inicial presentado en el guion?
-Se utiliza el método de Euler para resolver el problema de valor inicial.
¿Cuál es la ecuación diferencial del problema de valor inicial?
-La ecuación diferencial es y' = 12x + 1 con la condición inicial y(0) = 4.
¿Cuál es la solución analítica para el problema de valor inicial mencionado?
-La solución analítica es y = ln(2x) + 1.
¿Cómo se verifica la solución analítica para el problema de valor inicial?
-Se verifica evaluando la solución analítica en la condición inicial, donde y(0) debe ser igual a 4, y al derivar la solución para obtener y', debe coincidir con la ecuación diferencial dada.
¿Cuál es el valor inicial (x0) y su correspondiente valor de y (y0) en el método de Euler?
-El valor inicial es x_0 = 0 y el correspondiente valor de y es y_0 = 4.
¿Cómo se calcula el primer paso (x1) utilizando el método de Euler con un tamaño de paso h?
-Se calcula como x_1 = x_0 + h y y_1 = y_0 + h * f(x_0, y_0), donde f es la función dada en la ecuación diferencial.
¿Cuál es el tamaño del paso (h) utilizado en el primer ejemplo del método de Euler?
-El tamaño del paso utilizado en el primer ejemplo es h = 0.5.
¿Cómo se determina el valor aproximado de y en x1 utilizando el método de Euler?
-Se determina utilizando la fórmula y_1 = y_0 + h * f(x_0, y_0) y evaluando la función en los valores de x0 y y0.
¿Cuál es la diferencia entre los valores aproximados y los valores exactos para diferentes tamaños de paso (h)?
-Cuanto más pequeño sea el tamaño de paso (h), menor será el error relativo y más cercana estará la aproximación a la solución exacta.
¿Cómo se compara la solución numérica con la solución analítica en la gráfica?
-Se compara observando la cercanía de los puntos de la solución numérica (en forma de cuadros rojos) a la curva de la solución analítica (en azul).
¿Qué se concluye respecto al error relativo y el tamaño del paso en el método de Euler?
-Se concluye que un tamaño de paso más pequeño disminuye el error relativo, aunque aumenta el número de pasos necesarios para alcanzar un punto específico.

Outlines

00:00

📚 Resolución de problemas de valor inicial usando el método de Euler

El primer párrafo presenta un ejemplo de cómo resolver un problema de valor inicial utilizando el método de Euler. Se describe el problema de encontrar la función 'x(t)' dada la ecuación diferencial 'dx/dt = y(t)' y 'dy/dt = 12x + 1', con condiciones iniciales 'x(0) = 4' y 'y(0) = 0'. La solución analítica se muestra como 'x(t) = ln(2x(t) + 1)', la cual es verificada evaluando en 't=0'. Luego, se aplica el método de Euler para aproximar la solución numérica, utilizando un tamaño de paso 'h' y avanzando en pasos de 'h' para calcular 'x1', 'x2', y 'x3'. Se muestran los cálculos detallados y se compara la aproximación con la solución analítica.

05:01

📉 Comparación de la precisión del método de Euler con diferentes tamaños de paso

El segundo párrafo se enfoca en la comparación de la precisión del método de Euler para resolver el mismo problema, pero utilizando diferentes tamaños de paso 'h'. Se presentan los valores exactos y los valores aproximados para 'h' igual a 0.5 y 0.25, y se muestran los errores relativos porcentuales para cada caso. Se destaca cómo disminuir el tamaño de paso a 0.25 mejora la aproximación, reduciendo el error en comparación con 'h' igual a 0.5. Además, se incluye una gráfica que visualiza la solución analítica en azul y las aproximaciones numéricas en rojo y azul, respectivamente, para 'h' de 0.5 y 0.25, mostrando que la solución con 'h' más pequeño se acerca más a la solución analítica.

Mindmap

Keywords

💡Método de Euler

El Método de Euler es un algoritmo numérico utilizado para resolver problemas de valor inicial, como el mostrado en el script. Es una aproximación de la solución de una ecuación diferencial, donde se avanza en pasos pequeños (h) para calcular el valor de una función en un punto dado. En el video, se utiliza para resolver el problema de valor inicial de Jane, mostrando cómo se aproxima la solución analítica mediante este método.

💡Problema de valor inicial

Un problema de valor inicial es un tipo de problema matemático que involucra ecuaciones diferenciales y se busca encontrar una función que satisfaga una condición inicial específica. En el script, el problema de valor inicial de Jane es mencionado, donde se busca resolver la ecuación dada con una condición inicial de x(0) = 4.

💡Condición inicial

La condición inicial es un valor conocido de una función en un punto específico, que se utiliza para iniciar el proceso de solución de un problema de valor inicial. En el contexto del video, la condición inicial es x(0) = 4, que es el punto de partida para calcular la solución a la ecuación propuesta.

💡Solución analítica

Una solución analítica es la resolución exacta de un problema matemático, obtenida a través de fórmulas matemáticas clásicas. En el script, se menciona la solución analítica de x como el logaritmo natural de (2x), la cual se verifica evaluando en el punto de condición inicial y cumpliendo con la ecuación dada.

💡Derivada

La derivada es un concepto fundamental del cálculo que indica la tasa de cambio de una función con respecto a una variable. En el script, se utiliza la derivada para transformar la ecuación diferencial en una ecuación más manejable y para calcular el lado derecho de la ecuación en el Método de Euler.

💡Paso de integración (h)

El paso de integración, representado por 'h', es el intervalo que se utiliza para calcular el avance en el Método de Euler. Es la distancia que se recorre en el eje de las 'x' en cada iteración. El script muestra cómo se elige 'h' y cómo afecta la precisión de la aproximación numérica.

💡Aproximación numérica

La aproximación numérica se refiere a la solución de un problema matemático a través de métodos numéricos, que son aproximaciones de la solución exacta. En el video, se utiliza el Método de Euler para obtener una aproximación numérica de la solución del problema de valor inicial de Jane.

💡Error relativo

El error relativo es una medida de la precisión de una aproximación numérica, expresado como un porcentaje del valor verdadero. En el script, se calcula el error relativo para diferentes valores de 'h', mostrando cómo disminuye al reducir el tamaño del paso de integración.

💡Gráfica

Una gráfica es una representación visual de datos, en este caso, de la solución analítica y las aproximaciones numéricas. El script menciona la gráfica de la solución, donde se compara la solución analítica en azul con las aproximaciones numéricas en rojo y azul, para diferentes valores de 'h'.

💡Función

Una función es una relación matemática que asocia a cada elemento de un conjunto (dominio) un único elemento de otro conjunto (imagen). En el script, la función a resolver es central para el problema de valor inicial y para el Método de Euler, donde se evalúa en diferentes puntos para calcular la aproximación numérica.

Highlights

Ejemplo del método de Euler para resolver el problema de valor inicial de Jane.

Condición inicial: x(0) = 4 para la función 12x + 1.

Solución analítica: x = logaritmo natural de (2x^2).

Verificación de la solución analítica evaluando en x=0.

Derivada de la solución analítica: 2 * logaritmo natural de (4x).

Ecuación diferencial: 2y = 12x + 1.

Método de Euler para aproximar la solución numérica.

Valor inicial numérico: x0 = 0.5, y0 = 4.

Formula del método de Euler: y1 = y0 + h * f(x, y).

Evaluación de la función en x0 y y0: f(0, 4).

Resultado aproximado de y1: 5.03.

Avanzar en el tamaño de paso h: x1 = 0.5 + h.

Evaluación de la función en x1 y y1 para calcular y2.

Resultado aproximado de y2: 5.559.

Tabla de valores exactos y aproximados para diferentes valores de x.

Comparación de errores relativos al disminuir el tamaño de paso h.

Gráfica de la solución analítica y numérica para h = 0.5 y h = 0.25.

Mejora en la aproximación numérica al reducir h a 0.25.