HUBUNGAN SUDUT-SUDUT PADA DUA GARIS SEJAJAR YANG DIPOTONG OLEH SATU GARIS

Summary

This educational video introduces the concept of angles formed by two parallel lines intersected by a transversal. It covers various types of angles, including opposite angles, alternate interior angles, and corresponding angles, explaining their properties and relationships. The presenter demonstrates how to calculate the size of these angles, providing examples with step-by-step solutions. The video also encourages viewers to practice and learn about parallel line geometry while engaging with interactive quizzes. The aim is to help viewers understand and calculate angle measures easily, ensuring a solid grasp of geometry fundamentals.

Takeaways

• 😀 The video explains the concept of angles formed by two parallel lines intersected by a transversal.
• 😀 Four types of angles are discussed: opposite angles, alternate interior angles, alternate exterior angles, and supplementary angles.
• 😀 Opposite angles are equal in size, for example, angle O equals angle S.
• 😀 Alternate interior angles are equal, such as angle R equals angle P.
• 😀 Alternate exterior angles are equal, like angle O equals angle U.
• 😀 Supplementary angles add up to 180°, such as angle P and angle Q.
• 😀 The video demonstrates how to calculate angles using known values, such as subtracting from 180° to find the missing angle.
• 😀 If two angles are opposite each other, they are equal, as seen with angle O and angle Q, or angle P and angle R.
• 😀 The relationship between angles on a straight line, forming supplementary pairs, is emphasized with examples like angle P and angle Q summing to 180°.
• 😀 Practical examples are given to help students calculate unknown angles when some angles are provided.
• 😀 The video encourages viewers to engage by liking, subscribing, and pressing the notification bell for updates on new lessons.

Q & A

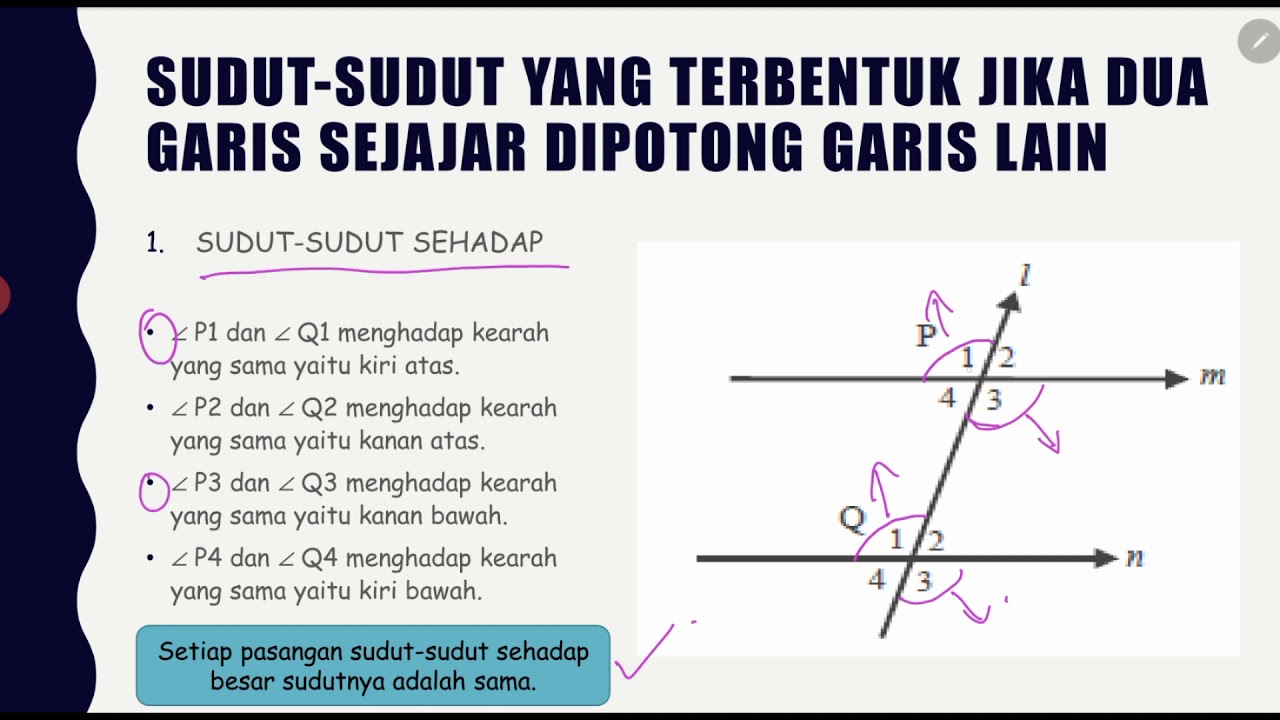
What are corresponding angles?

Corresponding angles are the angles that are on the same side of the transversal and in matching positions with respect to the two parallel lines. They are always equal.

Can you give an example of corresponding angles?

Yes, for example, ∠O is equal to ∠S, ∠P is equal to ∠E, and ∠R is equal to ∠V.

What are alternate interior angles?

Alternate interior angles are the angles that lie on opposite sides of the transversal and inside the two parallel lines. These angles are always equal.

What is the relationship between alternate exterior angles?

Alternate exterior angles are the angles formed on opposite sides of the transversal but outside the parallel lines. Like alternate interior angles, they are also equal.

What are vertically opposite angles?

Vertically opposite angles are the angles that are opposite each other when two lines intersect. These angles are always equal.

If ∠P = 65°, what is ∠T?

Since ∠P and ∠T are corresponding angles, they are equal. Therefore, ∠T is also 65°.

How do you calculate ∠Q if ∠P = 65°?

Since ∠P and ∠Q are supplementary (they form a straight line), their sum is 180°. So, ∠Q = 180° - 65° = 115°.

What is the relationship between ∠T and ∠V?

∠T and ∠V are vertically opposite angles, so they are equal. If ∠T = 60°, then ∠V also equals 60°.

If ∠P = 65°, how do you calculate ∠S?

∠P and ∠S are supplementary, meaning they add up to 180°. Therefore, ∠S = 180° - 65° = 115°.

Why are alternate interior angles equal?

Alternate interior angles are equal because they are formed by two parallel lines and a transversal. This relationship holds due to the properties of parallel lines and the transversal cutting them.