ÂNGULOS CORRESPONDENTES | ÂNGULOS FORMADOS POR RETAS PARALELAS CORTADAS POR UMA TRANSVERSAL|
Summary
TLDRIn this lesson, the instructor explores the relationships between angles formed by two parallel lines cut by a transversal. The focus is on corresponding angles, which are congruent and occupy the same position relative to the parallel lines and transversal. Through visual explanations, the instructor demonstrates how these angles are equal, offering an intuitive understanding of the concept. The video also touches on other related angle relationships, like alternate interior angles and supplementary angles, preparing viewers for upcoming exercises and further lessons on the topic.
Takeaways
- 😀 Understanding the concept of parallel lines and transversal: Two parallel lines are cut by a transversal, forming different types of angles.
- 😀 Corresponding angles are congruent: These angles are formed in the same relative position when a transversal crosses parallel lines.
- 😀 The importance of parallelism: The congruency of corresponding angles only occurs when the lines are truly parallel.
- 😀 Visual aids enhance comprehension: Diagrams are used to illustrate the relationships between the angles formed by the transversal and the parallel lines.
- 😀 Corresponding angles occur in pairs: Each angle formed by the transversal has a corresponding angle that shares the same measure.
- 😀 Alternate interior angles: These angles, while not the focus of the lesson, are another important concept to explore in future lessons.
- 😀 Angle naming conventions: Angles are named using letters (e.g., angle A, angle B) to help identify and relate them to one another.
- 😀 The sum of angles at intersections: When the transversal crosses two parallel lines, a total of 360 degrees is formed by the eight angles created.
- 😀 The role of congruent angles in geometry: Congruent angles (having the same measure) help solve various geometric problems and prove geometric theorems.
- 😀 Encouragement to practice: The teacher emphasizes the importance of practicing these concepts through exercises, which will follow in subsequent lessons.
Q & A
What are parallel lines?
-Parallel lines are two straight lines that never meet, regardless of how far they are extended. They are always the same distance apart.
What is a transversal in geometry?
-A transversal is a line that cuts across two or more other lines. In the context of parallel lines, a transversal intersects the parallel lines at an angle.
What are corresponding angles?
-Corresponding angles are pairs of angles that are in the same relative position at each intersection of a transversal and parallel lines. These angles are congruent, meaning they have the same measure.
Can you explain why corresponding angles are congruent?
-Corresponding angles are congruent because the transversal creates equal angles at each intersection with the parallel lines. The parallel nature of the lines ensures that the angles formed are symmetrical.
What are alternate interior angles?
-Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines. These angles are also congruent.
What is the significance of angle congruence when studying parallel lines and transversals?
-Angle congruence helps to establish relationships between angles formed by a transversal cutting parallel lines. This property is crucial for solving geometric problems involving parallel lines and angles.
What are co-interior angles?
-Co-interior angles are pairs of angles that are on the same side of the transversal and inside the parallel lines. These angles are supplementary, meaning their sum equals 180°.
Why is it important to understand the concept of parallel lines when studying angles?
-Understanding parallel lines is essential because many geometric properties, such as the congruence of corresponding angles and the supplementary nature of co-interior angles, are only valid when the lines are parallel.
What happens if the lines are not parallel?
-If the lines are not parallel, the relationships between the angles, such as congruence or supplementary properties, no longer hold true. The angles formed by a transversal and non-parallel lines will vary and cannot be generalized in the same way.
How can we classify the angles formed by a transversal cutting parallel lines?
-The angles formed can be classified into corresponding angles, alternate interior angles, and co-interior angles. These relationships help determine the angle measures based on the position of the lines and transversal.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Garis dan Sudut (5) | Hubungan Antar Sudut pada Dua Garis Sejajar | Matematika Kelas 7
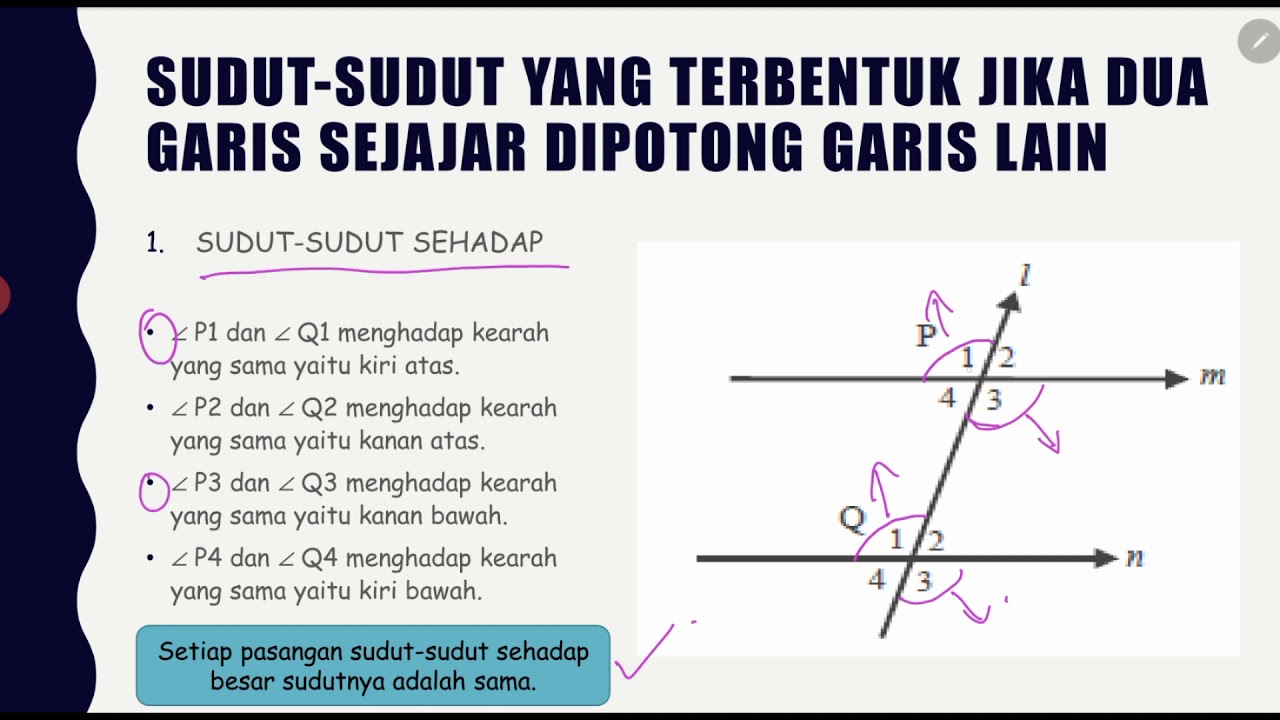
Kedudukan Dua Garis & Hubungan Antara Sudut dan Garis Kelas 7 SMP

Sudut pada Dua Garis Sejajar Kelas 7

Kupas Tuntas Sudut dan Garis (Sehadap, Bertolak belakang, dalam berseberangan dll)
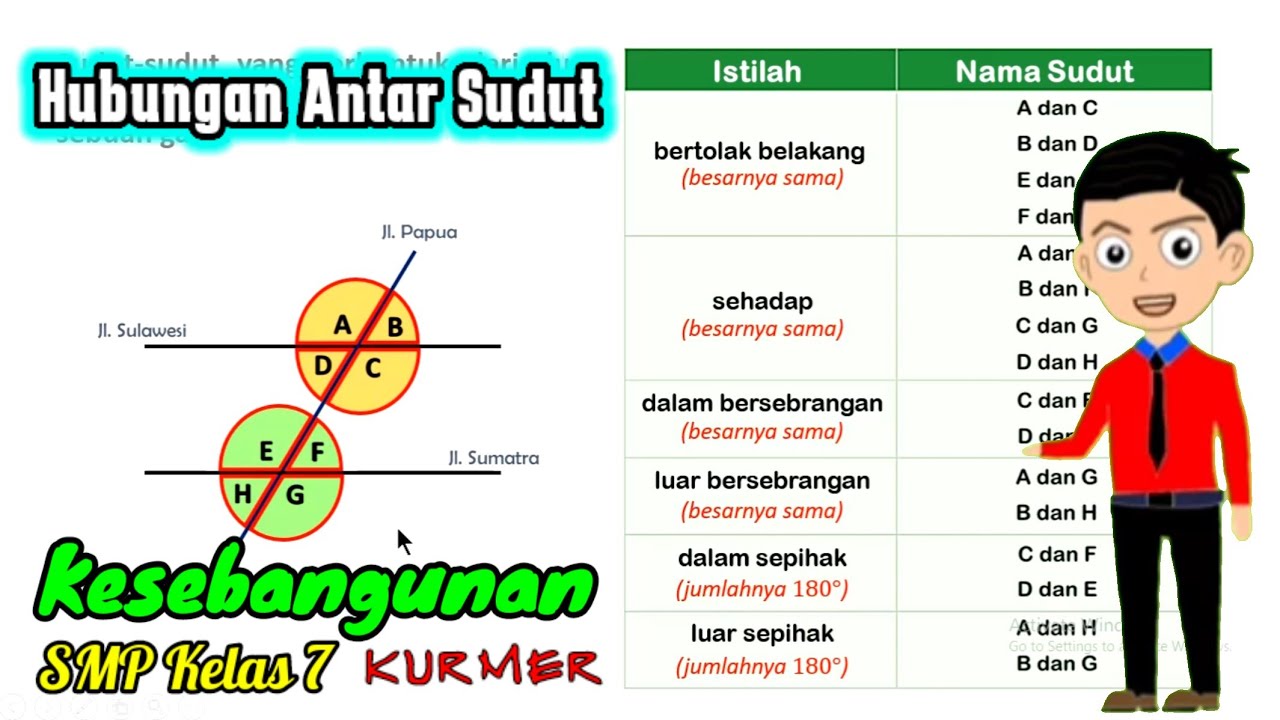
kesebangunan bagian 1 (hubungan antar sudut)

Pembahasan Mari Kita Periksa Garis Sejajar dan Segi Banyak Hal 115 Bab 4 Kelas 8 Kurikulum Merdeka
5.0 / 5 (0 votes)