Aplicaciones de los sistemas de ecuaciones. Ejemplo 1
Summary
TLDRIn this math tutorial, Jesús Grajeda explains how to solve a system of linear equations to determine the price of papayas and melons. The problem involves two transactions: buying two papayas and three melons for 85 pesos, and buying three papayas and two melons for 90 pesos. Jesús uses Cramer's Rule (determinants method) to solve the system, ultimately finding that each papaya costs 20 pesos and each melon costs 15 pesos. He emphasizes the importance of setting up equations correctly and encourages viewers to explore other methods of solving linear systems in previous videos.
Takeaways
- 😀 The video teaches how to solve a system of linear equations applied to a real-world problem.
- 😀 The problem involves finding the price of a papaya and a melon based on two different transactions.
- 😀 The first transaction consists of buying 2 papayas and 3 melons for 85 pesos.
- 😀 The second transaction consists of buying 3 papayas and 2 melons for 90 pesos.
- 😀 The variables are defined as P (price of a papaya) and M (price of a melon).
- 😀 Two equations are formulated from the problem: 2P + 3M = 85 and 3P + 2M = 90.
- 😀 The instructor chooses Cramer's Rule to solve the system using determinants.
- 😀 Determinants are calculated to find the values of P and M. The determinant of the system (Δ) is -5.
- 😀 The determinant of P (ΔP) is -100, and the determinant of M (ΔM) is -75.
- 😀 Using the formulas for Cramer's Rule, P = 20 pesos (price of a papaya) and M = 15 pesos (price of a melon).
- 😀 The instructor emphasizes that solving real-world problems with systems of equations can be simple once the equations are correctly formulated and the method is chosen.
Q & A
What type of mathematical problem is being solved in the video?
-The video focuses on solving a system of linear equations with two variables (2x2).
What is the context of the problem presented in the video?
-The problem involves purchasing papayas and melons with two different purchase scenarios, where the goal is to determine the price of each fruit.
How is the price of each fruit represented in the equations?
-The price of each papaya is represented by the variable 'P', and the price of each melon is represented by the variable 'M'.
What are the two equations used to solve the problem?
-The first equation is: 2P + 3M = 85, and the second equation is: 3P + 2M = 90.
What method does the speaker choose to solve the system of equations?
-The speaker chooses to solve the system of equations using Cramer's Rule, which involves determinants.
What is the determinant of the system of equations, and what does it represent?
-The determinant of the system, denoted as delta S, is calculated to be -5. It represents the overall determinant of the coefficients of the variables in the system.
How are the determinants for P and M calculated?
-The determinant for P (delta P) is calculated using the constants from the right-hand side of the equations and the coefficients of M. For M (delta M), the determinant is calculated similarly but swapping the coefficients of P with the constants.
What are the final values for P and M?
-The final value for P (the price of one papaya) is 20, and the final value for M (the price of one melon) is 15.
What does the speaker emphasize about solving applied problems like this one?
-The speaker emphasizes that correctly setting up the system of equations is crucial, and once that is done, solving the system using methods like Cramer's Rule makes the process straightforward.
What does the speaker encourage viewers to do after watching the video?
-The speaker encourages viewers to subscribe to the channel, share the video, and follow them on social media. Additionally, they stress that 'mathematics has your back.'
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Menyelesaikan Persamaan Linier dengan Matriks
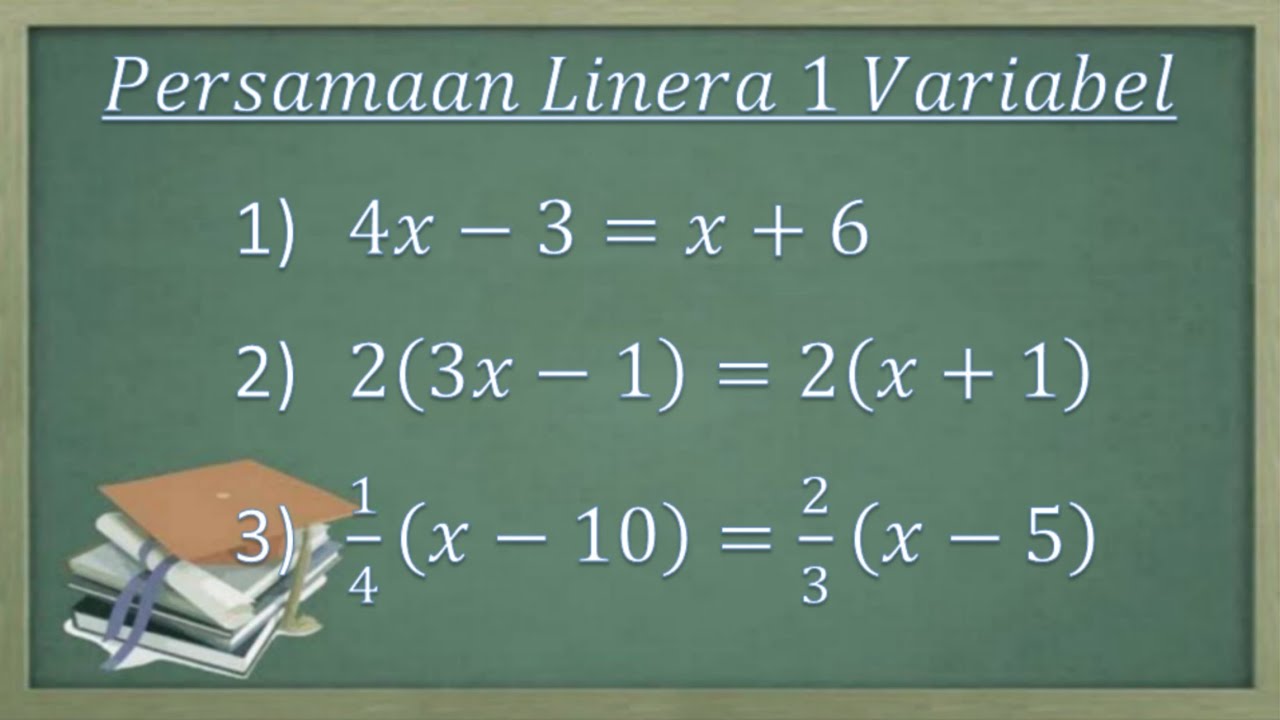
Sistem persamaan Linear satu variabel. Cara menentukan himpunan penyelesaiannya

Sistem persamaan linear tiga variabel dengan metode substitusi

SPLDV - Metode Eliminasi

Kinan menimbang bola yang ada di lemari sekolah. Pada penimbangan pertama, Kinan menimbang dua bo...
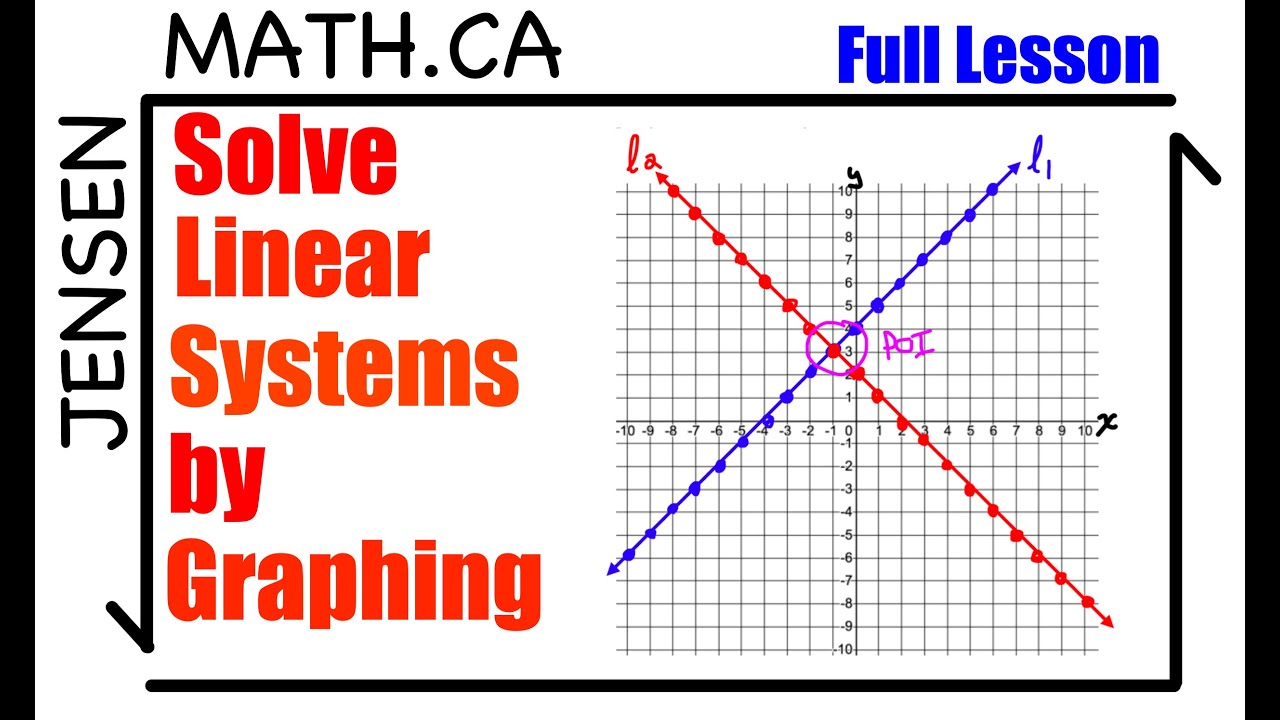
Solve a Linear System by Graphing | jensenmath.ca | grade 10
5.0 / 5 (0 votes)