RazonesTrigonométricas
Summary
TLDREn este video de la Universidad de Costa Rica, se enseña a los estudiantes a identificar las razones trigonométricas de un triángulo rectángulo. Se explican los términos hipotenusa, cateto opuesto y cateto adyacente, y se definen las tres razones básicas: seno, coseno y tangente, junto con sus correspondientes razones recíprocas. Se utiliza el teorema de Pitágoras para encontrar la hipotenusa y se presentan ejemplos prácticos para calcular las razones trigonométricas y sus valores recíprocos. El video también sugiere practicar con ángulos en radianes para comprobar la consistencia de los resultados.
Takeaways
- 📚 Este video es una lección de matemáticas de la Universidad de Costa Rica sobre trigonometría en triángulos rectángulos.
- 🔍 Se identifican los términos clave: ángulo agudo (Alfa), hipotenusa (M), cateto opuesto (opuesto a Alfa) y cateto adyacente (unido a Alfa).
- 📐 Se definen las razones trigonométricas básicas: seno (freno), coseno y tangente, relacionadas con las medidas de los lados del triángulo.
- 🔄 Se presentan las razones trigonométricas recíprocas: cosecante, secante y cotangente, que son inversas a las razones básicas.
- 🧠 Se utiliza la técnica 'socatóa' para recordar las tres razones trigonométricas básicas por sus iniciales.
- 📘 Se hace un ejemplo práctico para aplicar la teoría, donde se calcula la hipotenusa utilizando el teorema de Pitágoras.
- 📝 Se calculan las seis razones trigonométricas para un triángulo rectángulo dado, usando las medidas de los catetos y la hipotenusa.
- 🔢 Se pide a los estudiantes que calculen los valores de X e Y en otro ejemplo, donde se conoce el ángulo y se debe usar la relación con las razones trigonométricas.
- 📐 Se sugiere que se compruebe la consistencia de los resultados al utilizar ángulos en radianes.
- 👍 Se agradece la atención y se anima a la práctica adicional para mejorar la comprensión de la trigonometría en triángulos rectángulos.
Q & A
¿Qué es un triángulo rectángulo y cómo se relaciona con la trigonometría?
-Un triángulo rectángulo es un triángulo que tiene un ángulo de 90 grados. En la trigonometría, se utilizan las relaciones entre los lados y los ángulos de este tipo de triángulo para definir las razones trigonométricas.
¿Cuáles son los nombres de los lados de un triángulo rectángulo en relación con un ángulo Alfa?
-El lado opuesto al ángulo de 90 grados se llama hipotenusa. El lado opuesto al ángulo Alfa se llama cateto opuesto, y el lado que une el ángulo Alfa con el ángulo de 90 grados es el cateto adyacente.
¿Qué son las razones trigonométricas y cómo se definen?
-Las razones trigonométricas son relaciones matemáticas entre los ángulos y los lados de un triángulo rectángulo. Se definen como: el seno de Alfa es el cateto opuesto dividido por la hipotenusa, el coseno de Alfa es el cateto adyacente dividido por la hipotenusa y la tangente de Alfa es el cateto opuesto dividido por el cateto adyacente.
¿Qué son las razones trigonométricas recíprocas y cómo se relacionan con las básicas?
-Las razones trigonométricas recíprocas son las que se generan a partir de las tres razones básicas. La cosecante es el inverso del seno, la secante es el inverso del coseno y la cotangente es el inverso de la tangente.
¿Cómo se puede recordar las tres razones trigonométricas básicas?
-Se puede utilizar el acrónimo 'SOCATOA', que se forma con las iniciales de cada una de las razones: seno, coseno, tangente, cotangente, secante y cosecante.
¿Qué herramienta matemática se utiliza para calcular la hipotenusa de un triángulo rectángulo si se conocen los catetos?
-Se utiliza el teorema de Pitágoras, que establece que el cateto al cuadrado más el cateto al cuadrado es igual a la hipotenusa al cuadrado.
En el ejemplo dado, ¿cómo se calcula la hipotenusa si los catetos miden 3 y 5 unidades?
-Para calcular la hipotenusa, se utiliza la fórmula dada por el teorema de Pitágoras: hipotenusa = √(cateto1^2 + cateto2^2). En este caso, hipotenusa = √(3^2 + 5^2) = √(9 + 25) = √34.
Si se conoce el valor de la hipotenusa y el cateto opuesto en un ángulo Alfa, ¿cuál es la fórmula para calcular el seno de Alfa?
-El seno de Alfa se calcula dividiendo el cateto opuesto por la hipotenusa: seno(Alfa) = cateto_opuesto / hipotenusa.
En el segundo ejemplo del guión, ¿qué información adicional se proporciona para determinar los valores de X y Y?
-En el segundo ejemplo, se proporciona la medida de un ángulo (30 grados), la hipotenusa y se pide determinar los valores de X (cateto opuesto) y Y (cateto adyacente) utilizando las razones trigonométricas apropiadas.
¿Cómo se puede utilizar la razón seno para determinar el valor de X en el segundo ejemplo del guión?
-Dado que X es el cateto opuesto al ángulo de 30 grados, se puede utilizar la fórmula del seno: seno(30°) = X / hipotenusa. Conociendo el valor de la hipotenusa, se puede despejar X.
¿Qué es un buen ejercicio para comprobar la consistencia de los resultados al utilizar ángulos en radianes?
-Un buen ejercicio es calcular las razones trigonométricas utilizando ángulos en radianes y comparar los resultados con los obtenidos utilizando ángulos en grados para asegurar que no varían.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
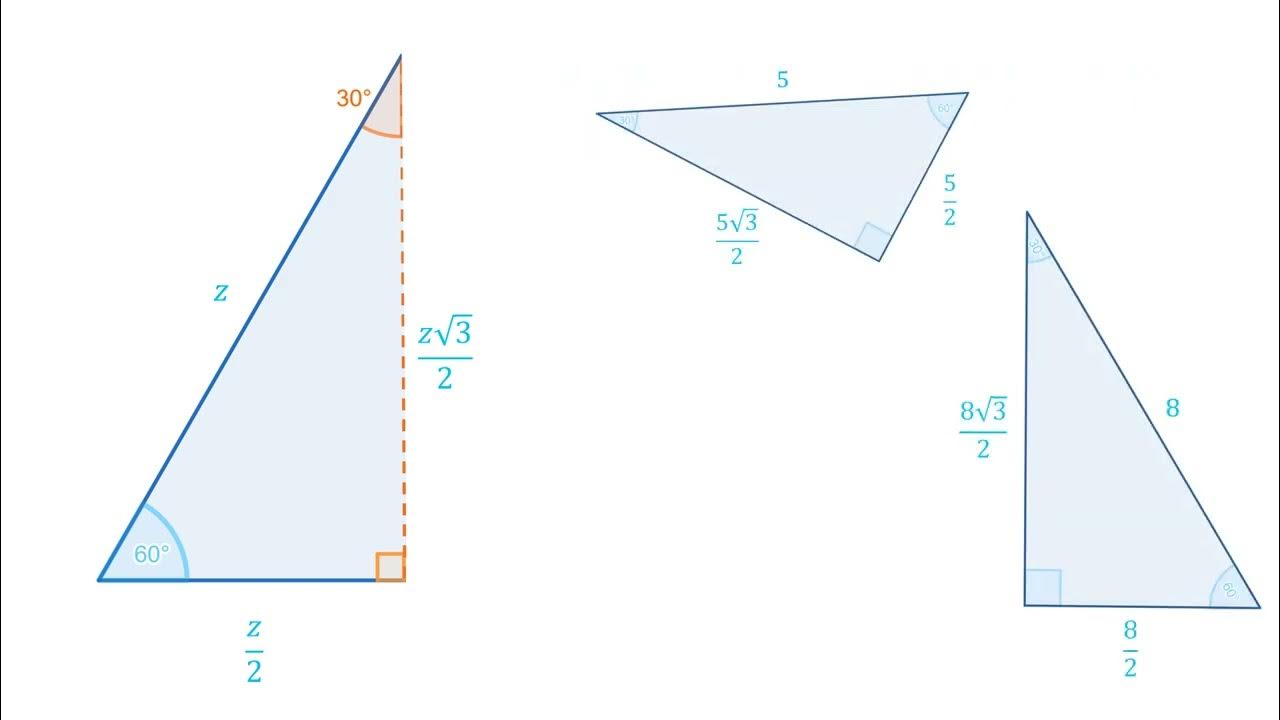
Razones Trigonométricas en Triángulos Especiales

Solucionar un triángulo rectángulo | Razones trigonométricas | Ejemplo 1
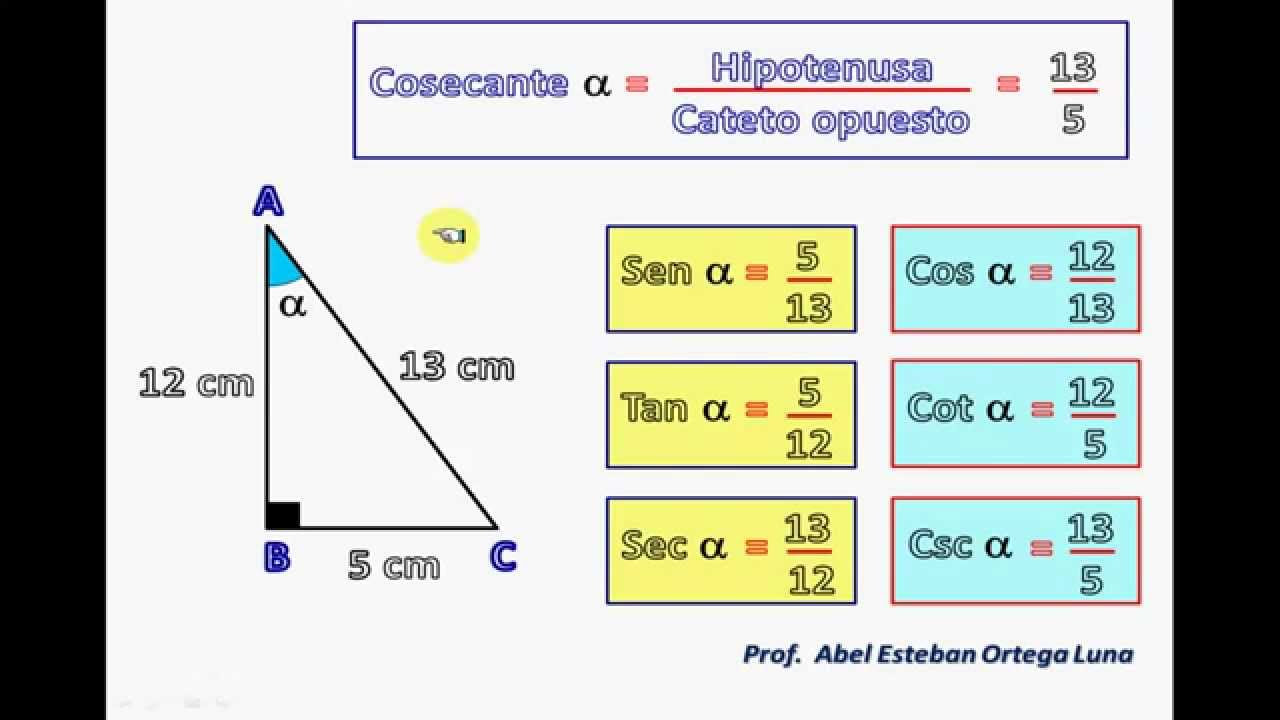
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Razones trigonométricas de un ángulo | Ejemplo 1

Razones: elevación depresión

Como calcular los lados de un triángulo rectángulo conociendo un lado y un angulo
5.0 / 5 (0 votes)
