Lec 02 - Rational Numbers

Summary

This lecture delves into the concept of rational numbers, distinguishing them from natural numbers and integers. It explains that rational numbers, often represented as fractions, can be expressed in multiple ways, unlike integers. The script highlights the process of reducing fractions to their simplest form by finding the greatest common divisor (GCD) through prime factorization. It also discusses the unique property of rational numbers being dense, meaning there is always another rational number between any two given rationals, contrasting with the discrete nature of integers. The lecture concludes by emphasizing the utility of rational numbers in arithmetic and comparisons, and their unique representation using the symbol Q.

Takeaways

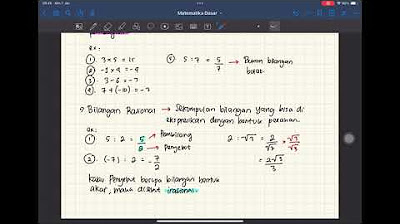
• 🔢 Rational numbers, also known as fractions, can be expressed as p divided by q, where both p and q are integers.
• 📏 The numerator (p) is the number above the fraction line, and the denominator (q) is the number below.
• 🌐 Rational numbers can be represented in multiple ways, unlike integers, which have a unique representation.
• 🔄 To compare or add rational numbers with different denominators, they must be converted to equivalent fractions with a common denominator.
• 🔢 The least common multiple (LCM) can be used to find a common denominator, but any common multiple will suffice.
• ➗ Rational numbers can be simplified to their reduced form by dividing both the numerator and the denominator by their greatest common divisor (GCD).
• 🔑 Prime factorization is a method used to find the GCD of two numbers, which helps in simplifying rational numbers to their reduced form.
• 🚫 Unlike integers, there is no concept of 'next' or 'previous' rational numbers because between any two rationals, another rational can always be found.
• 🔍 Rational numbers are dense on the number line, meaning there are no gaps between them, unlike integers which are discrete.
• 📚 The script uses the symbol 'Q' with double lines to denote the set of rational numbers, emphasizing their unique properties.
• ✂️ To summarize, rational numbers are ratios of two integers, they are not uniquely represented, and they lack a 'next' or 'previous' property due to their density.

Q & A

What is a rational number?

A rational number is a number that can be expressed as the quotient or fraction p/q, where p and q are integers, and q is not zero.

Why can't we represent 19 divided by 5 as an integer?

We cannot represent 19 divided by 5 as an integer because there is no integer k such that 5 times k equals 19.

How is the quantity 19 divided by 5 represented as a rational number?

The quantity 19 divided by 5 is represented as a rational number as 3 and four-fifths, or as the improper fraction 19/5.

What is the special symbol used to denote rational numbers?

The special symbol used to denote rational numbers is a double-lined Q, which looks somewhat unusual.

Why can the same rational number be written in many different ways?

The same rational number can be written in many different ways because you can multiply or divide both the numerator and the denominator by the same non-zero integer and the value of the fraction remains unchanged.

How can you compare two fractions with different denominators?

To compare two fractions with different denominators, you need to convert them into equivalent fractions with the same denominator, usually by finding a common multiple of the two denominators.

What is the least common multiple and how is it used in comparing fractions?

The least common multiple (LCM) is the smallest number into which both denominators of two fractions can be multiplied to become factors of that number. It is used to compare fractions by making their denominators the same.

What is the reduced form of a rational number and why is it preferred?

The reduced form of a rational number is when the numerator and denominator have no common factors other than 1. It is preferred because it provides a unique and simplified representation of the rational number.

How do you find the greatest common divisor (GCD) of two numbers?

You can find the GCD of two numbers by using prime factorization, identifying the common prime factors, and multiplying them together.

Why can't we talk about the next or previous rational number in the same way we do for integers?

We can't talk about the next or previous rational number because between any two rational numbers, there is always another rational number. This is due to the density of the rational numbers, unlike integers which are discrete.

What does it mean for numbers to be dense?

Numbers are dense when there are no gaps between them. In the context of rational numbers, this means that between any two rational numbers, you can always find another rational number, such as by taking their average.

Outlines

00:00

🔢 Introduction to Rational Numbers and Fractions

This paragraph introduces the concept of rational numbers, explaining that they are fractions represented as p divided by q, where p and q are integers. It highlights the difference between rational numbers and integers, noting that rational numbers can be written in multiple ways, unlike integers. The paragraph also explains how to represent non-integer division results, such as 19 divided by 5, as a fraction (3 and four-fifths). It introduces the notation Q for rational numbers and discusses the process of comparing and adding fractions with different denominators by finding a common denominator, such as using the least common multiple. The concept of equivalent fractions is also covered, demonstrating how to convert fractions to have the same denominator for these operations.

05:01

📉 Reducing Rational Numbers to Their Simplest Form

The second paragraph delves into the concept of reducing rational numbers to their simplest form, where there are no common factors between the numerator and the denominator. It explains that this is achieved by finding the greatest common divisor (gcd) of both the numerator and the denominator and dividing them by this number. The paragraph provides an example, converting 18/60 to its reduced form of 3/10, and explains how to find the gcd using prime factorization. It also touches on the property of integers having a distinct next and previous integer, contrasting this with the density of rational numbers, where there is always another rational number between any two given rationals, as demonstrated by taking the average of two numbers.

10:02

📚 Summary of Rational Numbers: Density and Unique Representation

The final paragraph summarizes the key points about rational numbers. It emphasizes that rational numbers are dense, meaning that between any two rationals, another rational number can always be found, unlike integers which are discrete with gaps between them. The paragraph also reiterates that rational numbers are ratios of two integers and that they do not have a unique representation because multiplying both the numerator and denominator by the same number results in an equivalent rational number. To achieve a unique representation, rational numbers are simplified to their reduced form, where the gcd of the numerator and denominator is 1. Lastly, it is highlighted that the concept of 'next' or 'previous' does not apply to rational numbers due to their dense nature, in contrast to the discrete nature of integers and natural numbers.

Keywords

💡Natural numbers

Natural numbers are the set of positive integers starting from 1 and going upwards. They are the most basic numbers used in counting and arithmetic. In the script, natural numbers are mentioned as a starting point for discussing numbers before moving on to integers and rational numbers.

💡Integers

Integers are a broader category of numbers that include natural numbers, their negatives, and zero. They are whole numbers and can be positive, negative, or zero. The script discusses integers in the context of division and how some divisions cannot result in an integer, leading to the concept of rational numbers.

💡Rational numbers

Rational numbers are numbers that can be expressed as a fraction where both the numerator and the denominator are integers, and the denominator is not zero. The script explains that rational numbers include fractions and can be written in many different equivalent forms. They are central to the video's theme as they are used to illustrate the concept of fractions, equivalence, and arithmetic operations.

💡Fraction

A fraction is a way of representing a part of a whole and is one of the forms a rational number can take. It consists of a numerator (the part) and a denominator (the whole). The script uses the example of 19 divided by 5 to introduce fractions and explains that fractions are used to represent numbers that cannot be expressed as whole integers.

💡Numerator and Denominator

In a fraction, the numerator is the top number, and the denominator is the bottom number. The script defines these terms and uses them to explain how fractions represent rational numbers. The terms are fundamental to understanding the structure of fractions and how they are used in arithmetic operations.

💡Least Common Multiple (LCM)

The Least Common Multiple is the smallest number that is a multiple of two or more numbers. In the context of the script, LCM is used to find a common denominator for fractions, which is necessary for comparing or adding fractions with different denominators. The script explains that finding an LCM is one way to make the denominators of fractions the same.

💡Greatest Common Divisor (GCD)

The Greatest Common Divisor is the largest number that divides two or more integers without leaving a remainder. The script discusses the GCD in relation to finding the reduced form of a rational number. By dividing both the numerator and the denominator by their GCD, one can express a fraction in its simplest form.

💡Reduced form

The reduced form of a rational number is when the fraction is expressed in its simplest form, where the numerator and the denominator have no common factors other than 1. The script emphasizes the importance of reduced form for representing rational numbers in a unique and simplified way.

💡Prime factorization

Prime factorization is the process of breaking down a number into its prime factors, which are the prime numbers that multiply together to result in the original number. The script uses prime factorization as a method to find the GCD of two numbers and to simplify fractions into their reduced form.

💡Dense numbers

Dense numbers refer to a set of numbers where between any two numbers, there is always another number from the set. The script explains that rational numbers are dense because between any two rational numbers, you can always find another rational number by taking their average. This is in contrast to integers, which are discrete and have no numbers between any two consecutive integers.

💡Discrete numbers

Discrete numbers are numbers in a set where each number has a unique successor and predecessor, and there are no numbers between any two consecutive numbers. The script contrasts discrete numbers, such as integers and natural numbers, with dense numbers like rational numbers, highlighting that discrete numbers have a clear 'next' and 'previous' property that rational numbers lack.

Highlights

Introduction to rational numbers and their representation as fractions.

Explanation of why 19 divided by 5 cannot be represented as an integer.

Rational numbers defined as fractions where both numerator and denominator are integers.

Introduction of the symbol Q to denote rational numbers.

Discussion on the non-unique representation of rational numbers.

Illustration of equivalent fractions with different denominators.

Explanation of the least common multiple in comparing fractions.

Process of converting fractions to a common denominator for addition.

The concept of finding a rational number's reduced form by eliminating common factors.

Use of prime factorization to determine the greatest common divisor (gcd).

The property of integers having a next and previous integer.

Contrast between discrete integers and dense rational numbers.

Explanation of why there is no 'next' or 'previous' rational number.

Demonstration of finding a rational number between any two given rationals by averaging.

Summary of the properties and representation of rational numbers.

The importance of reduced form in unique representation of rational numbers.

Transcripts

So, now first lecture on Numbers; we looked at natural numbers and integers.

So, now, let see what happens when we try to divide.

So, let us look at the rational numbers.

So, we said that we cannot represent 19 divided by 5 as an integer because we cannot find

a number k such that 5 times k is 19.

So, as we know the way we deal with this is to represent this quantity as a fraction.

So, we say that 19 divided by 5 is 3 and four-fifths.

So, this number 3 and four-fifths is an example of a rational number.

So, rational number what we usually called fractions in school, a rational number is

something that can be written as p divided by q; where, p and q are both integers.

So, as you probably remember from school, the number on the top is called the numerator.

So, p divided by q; p is called the numerator and q is called the denominator .

So, just like we had the symbols n and z to represent the natural numbers and the integers,

we have a special symbol which is somewhat unusual which is a Q . So, Q stands for the

rational numbers and again, to just say it is a special Q, we write these double lines

on sides.

So, this Q with these fat boundaries denotes the rational numbers.

So, one thing about the rational numbers is that the same number can be written in many

different ways.

Now, this is not true of integers.

Of course, we are not talking about changing base from binary to decimal or something.

But if you write a 7, there is only one way to write 7 fix, if you are fix the notation

that you are using for writing numbers.

With rational numbers, this is not true because there are many ways of writing p by q such

that p by q is actually a same number.

So, for instance if we take the number 3 by 5, then we all know that 3 by 5 is the same

as 6 by 10 and this is the same as 30 by 50.

So, when we take a rational number and multiply it by something the same quantity on the top

and the bottom, so, 3 by 2, 3 times 2 and 5 times 2, we get the same number; 6 by 10

or 3 times 10 and 5 times 10, we get the same number 30 by 50.

So, this is sometimes a nuisance, but it is also sometimes useful.

Now, there is no reasonable way to compare two numbers like say 3 by 5 and 3 by 4 or

2 by 5 and 3 by 4.

If we have two fractions which have different denominators, there is no way to directly

compare them.

So, the only way to compare them is to somehow convert them into equivalent fractions such

that they have the same denominator.

So, the usual way is just to find a number such that both the denominators multiply into

that number are factors of that number.

Now, you can find the smallest such number which is called the least common multiple;

but you can find any number of this form.

So, for instance, if you want to add 3 by 5 and 3 by 4, now you cannot do that directly;

but you know that 20 is a number which divides which which is a multiple of both 5 and 4.

So, you can represent 3 by 5 as equivalently as 12 by 20; you can represent 3 by 4 equivalent.

So, this is equivalent and this is equivalent.

So, you have converted these numbers into a different fraction of the same number; but

this new representation has the same denominator.

And now once, the two denominator that the same, you can add the numerators and you can

get 12 plus 15 is 27 by 20.

So, this kind of manipulation requires the denominators to be the same and therefore,

its actually extremely useful that we can write the same rational number in many different

ways.

The same is to we want to compare two numbers.

If we want to check whether 3 by 5 is bigger or smaller than 3 by 4, there is no way to

do it directly.

What we have to do is again take the denominators and make them the same and then, say that

12 by 20 is less than 15 by 20 because you are dividing something 20 parts and you are

taking 12 of them, that is less than taking 15.

Now, as I said there is no reason why this must be the smallest one.

So, for instance you could take a bigger number like 100 right.

So, 5 goes into 100 and 5 goes 4 also goes into 100.

So, we could also say that 3 by 5 is the same as 60 by 100 and 4, 3 by 4 is the same as

75 by 100 and therefore, since 60 is less than 75; 60 by 100 is less than 75 by 100

and therefore, 3 by 5 is less than 3 by 4 . So, it is not really important that the

denominator is the smallest common multiple of the two denominators; but it must be some

common multiple so that you can bring it all to a common number that you can then compare.

So, we saw that representation is not unique for rational numbers.

So, how do we find actually the best way to represent a rational number?

So, normally if you are not using it for some arithmetic operation of some comparison, we

would prefer to have it in a reduced form.

So, the reduced form of a rational number is one, where there are no common multiples

between the common factors between the top and the bottom.

So, p by q is of the form, where we cannot find any factor f such that f divides p and

f divides q.

So, for instance, if we take 18 by 60, then its reduced form will be 3 by 10.

Notice that 3 is of the form 3 times 1 and 10 is of the form 5 times 2 times 1.

So, therefore, there is no common factor between the top and the bottom and therefore, this

is in reduced form.

So, this is called the greatest common divisor problem.

So, we want to find the largest number which divides both the top and the bottom; both

the numerator and the denominator, divide them both by this and then come to something

in the reduced form.

So, in this case, what we are saying is that the gcd of 18 and 60 is actually 6 and we

can do this using our prime factorization that we talked about before.

So, if we look at prime factorization for 18, then 18 is 2 times 3 times 3 right; its

2 times 3 is 6 times 3 is 18 and the prime factorization of 60 is 2 times 2 times 3 times

5; its 4 into 3, 12 into 5 . So, now, you can look at what are common.

So, we have one 2 here and one 2 here.

So, we can say that this is part of the same factor, we have one 3 here and another 3 there.

The second 2 is not present in the first term.

So, we have a 2 and 3 and 18 which are factors.

We have a 2 and 3 in 60 which are factors and this gives us the fact that 6 is a common

factor.

There is no bigger common factor because we want to assemble a bigger common factor, we

have to pull out one more prime from each side; but there is no prime left which is

present on both sides.

3 is there in 18; 2 and 5 are there on 60, but we do not have a matching one of the other

side right.

So, this way, the common prime factors are one 2 and one 3 and so, 2 times 3 equal to

6 is the gcd.

Now, this is not the best way to find the gcd, there are more efficient ways to find

the gcd.

But this intuitively tells us what the gcd is.

You take the prime factorization of both the numbers and you collect together all the primes

that occur in both the numbers, the same number of times.

So, here is another interesting property about rational numbers.

Now, for each integer, we know intuitively that there is something which is the next

integer and the previous integer.

If I tell you 22 and ask you what is the next integer?

Then, you will know it is 23.

What is the previous one?

It will be 21.

So, for every integer m, the next one is m plus 1 and the previous one is m minus 1 and

it does not matter, if this is positive or negative.

So, for instance if I am at 17, then the next integer is 18, the previous one is 16 right.

If I am at minus 1, then the next integer is 0 and the previous integer is minus 2.

So, I can always take the integer that I am at, add 1 and get the next integer, subtract

1 you will get the previous integer.

So, the property of this next and previous is that there is nothing in between right.

So, there is no integer between m and m plus 1, there is no integer between m and m minus

1.

So, that is what next means, it is not some bigger integer or some smaller integer.

It is the immediate neighbour in the integer of the in this number line.

Now, what about rationals?

Is it possible to talk about the next and the previous rational number?

Now, it turns out that this is not possible for a very simple reason .

So, between any two rationals, we can always find another one because we can always take

the average of 2 numbers.

So, remember that if you take the average of any 2 numbers, then it must be between

those 2 numbers right because it is the sum of the numbers divided by 2.

So, the average cannot be smaller than both or cannot be bigger than both.

So, if the 2 numbers are not the same, then it must lie strictly between them.

If the numbers are the same, then the average is the same.

So, if somebody has 37 marks and 37 marks, then their average marks is 37.

But if they have 37 marks and 52 marks, even without calculating the average, you know

that their average is bigger than 37, but smaller than 52 right.

So, in the same way, if I give you 2 fractions m by n and p by q and I tell you that m by

n is smaller than p by q.

Remember that in order to do this, we would have to normally get the denominators to be

the same and so on.

But supposing I know that m by n is smaller than p by q.

So, I know that say m by n is here and I know that say p by q is here and supposing you

claim that m by n and p by q are adjacent, that is p by q is the next rational after

m by n.

Well, I will say no; let me take these 2 numbers and find its average right.

So, this average now is also a rational number because you can also represent it as another

p; p or a by b right.

If you just workout this m by n plus p by q divided by 2, you can simplify this whole

expression and you will get a new number which is also of the form a by b.

So, this is also a rational number and this rational number as we argued must be between

the 2 numbers and therefore, between any 2 rational numbers by just taking the average

of the mean of the 2 numbers, I can find another one .

So, in other words, the rational numbers are dense right.

So, dense in the usual sense, so dense just means that they are closely packed together.

So, so, basically you cannot find any gaps in the rational numbers because any between

any 2 rational numbers, you will find another rational number and this is not true of the

integers because we saw that in the number line, there is a gap between m and m plus

1, there is no integer there right.

So, we say that the rational numbers are dense and conversely, we say that the integers and

the natural numbers are discrete.

So, a discrete set has this kind of next property and a dense set has no next property between

any 2 numbers, will find another number right.

To summarize, we use this funny symbol Q to denote the rational numbers and a rational

number is just the ratio.

So, that is where it comes from actually; so, ratio.

So, rational number comes from the word ratio and so, it is a ratio of 2 integers p divided

by q.

Now, there is no unique representation of a rational number because we can multiply

both the numerator and the denominator by the same quantity and get a new rational number

which is exactly the same in terms of the quantity that it represents.

And we use this fact for things like arithmetic and comparisons, but if we really want to

talk about rational numbers in a canonical way, in a unique way; then, we get this reduced

form, where we cancel out the common factors using prime factorization.

So, that we get a number whose gcd of the numerator and the denominator is 1.

And finally, we saw that we cannot talk about the next or the previous rational number because

between any 2 rational numbers, there is another rational number.

In particular, if you take the average of the 2 numbers, you will find a number that

is in between.

So, unlike the integers and the natural numbers which are discrete for which next and previous

makes sense; for the rational numbers, there is no such quantity.