Solución de un sistema de 3x3 método de Gauss | Ejemplo 1
Summary
TLDREn este video, se explica detalladamente el método de Gauss para resolver sistemas de ecuaciones lineales. A través de ejemplos prácticos, se muestran los pasos de organización de las ecuaciones, la aplicación de operaciones fila para reducir la matriz a una forma triangular superior, y cómo resolver las incógnitas paso a paso. El enfoque pone énfasis en la importancia de las verificaciones para asegurar la precisión de la solución, mientras se dan recomendaciones sobre cómo evitar errores comunes y simplificar el proceso, incluso cuando las operaciones parecen sencillas.
Takeaways
- 😀 La eliminación de Gauss es un método útil para resolver sistemas de ecuaciones lineales 3x3.
- 😀 El proceso comienza organizando las ecuaciones en forma estándar y luego formando la matriz aumentada.
- 😀 Se aplican operaciones de fila para convertir la matriz en una forma triangular superior, donde se crean ceros debajo de la diagonal principal.
- 😀 Se recomienda realizar cambios de signo multiplicando toda la ecuación por -1 si la variable está acompañada de un signo negativo.
- 😀 El uso de operaciones de fila como la sustitución permite eliminar variables de las ecuaciones, simplificando el sistema.
- 😀 Una vez que se tiene la forma triangular, se puede realizar la sustitución hacia atrás para encontrar los valores de las variables.
- 😀 Comprobar la solución sustituyendo los valores en las ecuaciones originales asegura que la respuesta sea correcta.
- 😀 El proceso de eliminación de Gauss no solo ayuda a encontrar la solución, sino también a visualizar cómo interactúan las ecuaciones.
- 😀 Se enfatiza la importancia de no confiarse en operaciones sencillas y de verificar los resultados para evitar errores.
- 😀 Al finalizar, se recomienda practicar más para mejorar la comprensión de la eliminación de Gauss y su aplicación en tareas y evaluaciones.
- 😀 Es esencial ser cuidadoso al realizar operaciones con fracciones o decimales para evitar errores en el cálculo final.
Q & A
¿Qué método se utiliza en el video para resolver el sistema de ecuaciones?
-El video utiliza el método de eliminación de Gauss, que transforma el sistema de ecuaciones en una forma triangular superior para facilitar la resolución mediante sustitución hacia atrás.
¿Cuál es el primer paso en la eliminación de Gauss?
-El primer paso es organizar las ecuaciones y luego escribirlas en forma de matriz aumentada, donde se incluyen tanto los coeficientes de las variables como las constantes de las ecuaciones.
¿Qué se busca lograr con las operaciones de fila durante el proceso?
-El objetivo es transformar la matriz en una forma triangular superior, donde todos los elementos por debajo de la diagonal principal sean cero.
¿Qué operación se realiza para eliminar los términos debajo del primer pivote?
-Se realizan operaciones de fila como restar múltiplos de la primera fila de las filas inferiores para eliminar los términos debajo del pivote (el primer elemento no cero en la primera columna).
¿Por qué es importante cambiar el signo de la ecuación cuando se tiene un número negativo al despejar una variable?
-Es importante multiplicar toda la ecuación por -1 cuando se tiene un signo negativo en la variable para evitar errores y facilitar el despeje de la variable, cambiando todos los signos en la ecuación.
¿Cómo se verifica si la solución encontrada es correcta?
-Se verifica sustituyendo los valores de las variables encontradas en las ecuaciones originales. Si las igualdades se mantienen, entonces la solución es correcta.
¿Qué se debe hacer al final del proceso de eliminación de Gauss?
-Al final del proceso, se realiza una sustitución hacia atrás, comenzando con la última variable, para encontrar las soluciones de las otras variables en orden, de abajo hacia arriba.
¿Cómo se soluciona el sistema de ecuaciones después de obtener la matriz triangular superior?
-Después de obtener la matriz triangular superior, se resuelve el sistema mediante sustitución hacia atrás. Se empieza con la última fila (para encontrar z) y luego se sustituye en las filas anteriores para obtener los valores de las otras variables.
¿Qué se recomienda hacer si se encuentra con un sistema muy sencillo?
-Si el sistema es sencillo, es recomendable comprobar las soluciones sustituyendo las variables encontradas en las ecuaciones originales para asegurarse de que las igualdades se cumplan.
¿Cuál es la importancia de realizar operaciones cuidadosas durante el proceso de eliminación de Gauss?
-Es crucial realizar las operaciones cuidadosamente, ya que incluso errores pequeños en los cálculos pueden llevar a resultados incorrectos, especialmente cuando se trabaja con ecuaciones aparentemente sencillas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
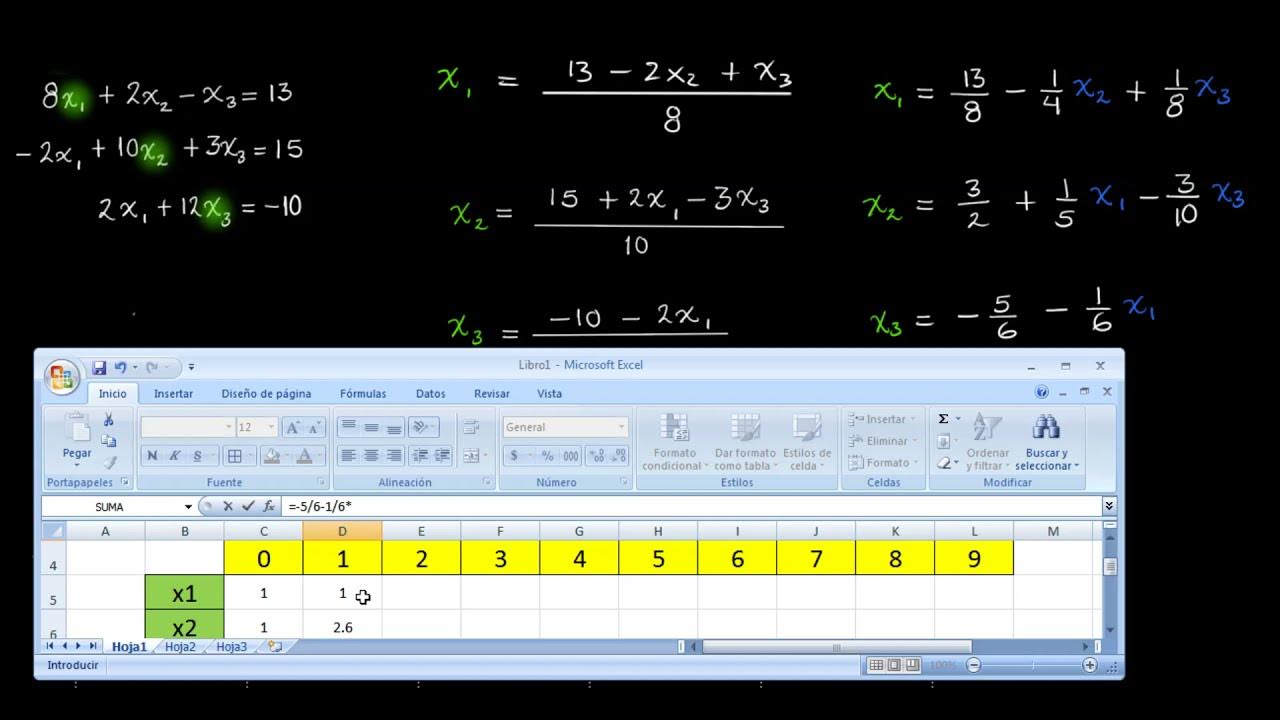
Método de Gauss Seidel: Teoría, ejemplo "a mano" y aplicación en hoja de cálculo

🛑 MÉTODO DE GAUSS JORDAN | SISTEMAS DE ECUACIONES 2X2 (paso a paso) Juliana la Profe

▷ Сómo resolver un sistema de ecuaciones por el MÉTODO DE GAUSS JORDAN paso a paso

Método de Reducción - Sistema de Ecuaciones Lineales 3x3 | Ejercicio 1

01. Sistemas de ecuaciones lineales, 2 variables | Álgebra Lineal

Matemáticas Video 2 8
5.0 / 5 (0 votes)
